Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-11T03:34:41.136Z Has data issue: false hasContentIssue false
  • English
  • Français

PRENEX NORMAL FORM THEOREMS IN SEMI-CLASSICAL ARITHMETIC

Part of: General logic Proof theory and constructive mathematics

Published online by Cambridge University Press:  11 June 2021

MAKOTO FUJIWARA  and
TAISHI KURAHASHI
MAKOTO FUJIWARA
Affiliation:
SCHOOL OF SCIENCE AND TECHNOLOGY MEIJI UNIVERSITY, 1-1-1 HIGASHI-MITA, TAMA-KU, KAWASAKI-SHI214-8571KANAGAWA, JAPANE-mail:makotofujiwara@meiji.ac.jp
TAISHI KURAHASHI
Affiliation:
GRADUATE SCHOOL OF SYSTEM INFORMATICS KOBE UNIVERSITY, 1-1 ROKKODAI, NADA 657-8501 KOBE, JAPANE-mail:kurahashi@people.kobe-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Akama et al. [1] systematically studied an arithmetical hierarchy of the law of excluded middle and related principles in the context of first-order arithmetic. In that paper, they first provide a prenex normal form theorem as a justification of their semi-classical principles restricted to prenex formulas. However, there are some errors in their proof. In this paper, we provide a simple counterexample of their prenex normal form theorem [1, Theorem 2.7], then modify it in an appropriate way which still serves to largely justify the arithmetical hierarchy. In addition, we characterize a variety of prenex normal form theorems by logical principles in the arithmetical hierarchy. The characterization results reveal that our prenex normal form theorems are optimal. For the characterization results, we establish a new conservation theorem on semi-classical arithmetic. The theorem generalizes a well-known fact that classical arithmetic is 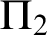$\Pi _2$ -conservative over intuitionistic arithmetic.

Keywords

Prenex normal form theoremsemi-classical arithmeticintuitionistic arithmetic

MSC classification

Primary: 03B20: Subsystems of classical logic (including intuitionistic logic)
Secondary: 03F03: Proof theory, general 03F30: First-order arithmetic and fragments 03F50: Metamathematics of constructive systems
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 3 , September 2021 , pp. 1124 - 1153
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akama, Y., Berardi, S., Hayashi, S., and Kohlenbach, U., An arithmetical hierarchy of the law of excluded middle and related principles, Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science (LICS’04), Turku, Finland, IEEE, 2004, pp. 192–201.10.1109/LICS.2004.1319613CrossRefGoogle Scholar
Friedman, H., Classically and intuitionistically provably recursive functions, Higher Set Theory (Müller, G. H. and Scott, D. S., editors), Springer, Berlin/Heidelberg, 1978, pp. 21–27.10.1007/BFb0103100CrossRefGoogle Scholar
Fujiwara, M. and Kohlenbach, U., Interrelation between weak fragments of double negation shift and related principles, this Journal, vol. 83 (2018), no. 3, pp. 991–1012.Google Scholar
Fujiwara, M. and Kurahashi, T., Conservation theorems on semi-classical arithmetic, preprint, 2020.Google Scholar
Hayashi, S. and Nakata, M., Towards limit computable mathematics, Types for Proofs and Programs (Callaghan, P., Luo, Z., McKinna, J., and Pollack, R., editors), R. Pollack Edn, Springer, Berlin/Heidelberg, 2002, pp. 125–144.10.1007/3-540-45842-5_9CrossRefGoogle Scholar
Kohlenbach, U., Applied Proof Theory: Proof Interpretations and their Use in Mathematics, Springer Monographs in Mathematics, Springer-Verlag, Berlin, Germany, 2008.Google Scholar
Kohlenbach, U. and Safarik, P., Fluctuations, effective learnability and metastability in analysis. Annals of Pure and Applied Logic, vol. 165 (2014), no. 1, pp. 266–304, The Constructive in Logic and Applications (A. Nerode and M. Fitting, editors).10.1016/j.apal.2013.07.014CrossRefGoogle Scholar
Troelstra, A. S. (editor), Metamathematical Investigation of Intuitionistic Arithmetic and Analysis , Lecture Notes in Mathematics, vol. 344, Springer-Verlag, Berlin, New York, 1973.10.1007/BFb0066739CrossRefGoogle Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics, An Introduction, vol. 1, Studies in Logic and the Foundations of Mathematics, vol. 121, North Holland, Amsterdam, 1988.Google Scholar
van Dalen, D., Logic and Structure , fifth Edn., Universitext, Springer-Verlag, London, 2013.10.1007/978-1-4471-4558-5CrossRefGoogle Scholar