Article contents
A probabilistic interpolation theorem
Published online by Cambridge University Press: 12 March 2014
Extract
The probability logic  is a logic with a natural interpretation on probability spaces (thus, a logic whose model theory is part of probability theory rather than a system for putting probabilities on formulas of first order logic). Its exact definition and basic development are contained in the paper [3] of H. J. Keisler and the papers [1] and [2] of the author. Building on work in [2], we prove in this paper the following probabilistic interpolation theorem for
is a logic with a natural interpretation on probability spaces (thus, a logic whose model theory is part of probability theory rather than a system for putting probabilities on formulas of first order logic). Its exact definition and basic development are contained in the paper [3] of H. J. Keisler and the papers [1] and [2] of the author. Building on work in [2], we prove in this paper the following probabilistic interpolation theorem for  .
.
Let L be a countable relational language, and let A be a countable admissible set with ω ∈ A (in this paper some probabilistic notation will be used, but ω will always mean the least infinite ordinal). 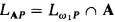 is the admissible fragment of
is the admissible fragment of  corresponding to A. We will assume that L is a countable set in A, as is usual in practice, though all that is in fact needed for our proof is that L be a set in A which is wellordered in A.
corresponding to A. We will assume that L is a countable set in A, as is usual in practice, though all that is in fact needed for our proof is that L be a set in A which is wellordered in A.
Theorem. Let ϕ(x) and ψ(x) be formulas of LAP such that

where ε ∈ [0, 1) is a real in A (reals may be defined in the usual way as Dedekind cuts in the rationals). Then for any real d > ε¼, there is a formula θ(x) of (L(ϕ) ∩ L(ψ))AP such that
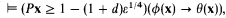
and
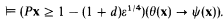
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 1
- Cited by

