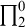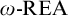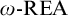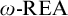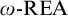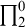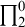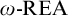1 Introduction
In the study of the arithmetic degrees (the degree structure induced by relative arithmetic definability,
![]() $\leq _{\mathbf {a}}$
) the
$\leq _{\mathbf {a}}$
) the
![]() $\omega \text {-REA}$
sets play a role analogous to the role the r.e. degrees play in the study of the Turing degrees. This analogy holds both as a matter of structure (e.g., the arithmetic jump is an
$\omega \text {-REA}$
sets play a role analogous to the role the r.e. degrees play in the study of the Turing degrees. This analogy holds both as a matter of structure (e.g., the arithmetic jump is an
![]() $\omega \text {-REA}$
operation and the jump is an r.e. operation) and as a way to approach constructions. For instance, just as the r.e. sets allow us to characterize the range of the Turing jump on
$\omega \text {-REA}$
operation and the jump is an r.e. operation) and as a way to approach constructions. For instance, just as the r.e. sets allow us to characterize the range of the Turing jump on
![]() $\mathscr {D}({\mathbf {0}}')$
(the Turing degrees less than or equal to
$\mathscr {D}({\mathbf {0}}')$
(the Turing degrees less than or equal to
![]() ${\mathbf {0}}'$
) via the Shoenfield jump inversion [Reference Shoenfield13] the
${\mathbf {0}}'$
) via the Shoenfield jump inversion [Reference Shoenfield13] the
![]() $\omega \text {-REA}$
sets allow us to similarly identify the range of the arithmetic jump on
$\omega \text {-REA}$
sets allow us to similarly identify the range of the arithmetic jump on
![]() $\mathscr {D}_{\mathbf {a}}({{\mathbf {0}}_{\mathbf {a}}}')$
with the degrees of the sets
$\mathscr {D}_{\mathbf {a}}({{\mathbf {0}}_{\mathbf {a}}}')$
with the degrees of the sets
![]() $\omega \text {-REA}$
in
$\omega \text {-REA}$
in
![]() ${{\mathbf {0}}_{\mathbf {a}}}'$
[Reference Simpson14].
${{\mathbf {0}}_{\mathbf {a}}}'$
[Reference Simpson14].
However, while the Turing degrees generally and the degrees of the r.e. sets specifically have been extensively studied much less is known about the arithmetic degrees and even less about the role of the
![]() $\omega \text {-REA}$
sets in that structure. Even seemingly basic questions remain open. For instance, whether or not there are any
$\omega \text {-REA}$
sets in that structure. Even seemingly basic questions remain open. For instance, whether or not there are any
![]() $\omega \text {-REA}$
sets of minimal arithmetic degree remains an open question. The analogy between the r.e. sets and the Turing degrees and the
$\omega \text {-REA}$
sets of minimal arithmetic degree remains an open question. The analogy between the r.e. sets and the Turing degrees and the
![]() $\omega \text {-REA}$
sets suggests that
$\omega \text {-REA}$
sets suggests that
![]() $\omega \text {-REA}$
sets of minimal arithmetic degree shouldn’t exist. However, it is already known that the analogy is imperfect as there is a minimal pair (in the arithmetic degrees) of
$\omega \text {-REA}$
sets of minimal arithmetic degree shouldn’t exist. However, it is already known that the analogy is imperfect as there is a minimal pair (in the arithmetic degrees) of
![]() $\omega \text {-REA}$
sets which join to
$\omega \text {-REA}$
sets which join to
![]() ${{\mathbf {0}}_{\mathbf {a}}}'$
[Reference Simpson14] in contrast to the non-diamond theorem in the r.e. degrees [Reference Lachlan8].
${{\mathbf {0}}_{\mathbf {a}}}'$
[Reference Simpson14] in contrast to the non-diamond theorem in the r.e. degrees [Reference Lachlan8].
While we don’t settle the existence of an
![]() $\omega \text {-REA}$
set of minimal arithmetic degree in this paper we make what we believe is an important step in that direction by proving the following result (and thereby presenting an alternate solution to Question 62 in [Reference Friedman2] by providing a
$\omega \text {-REA}$
set of minimal arithmetic degree in this paper we make what we believe is an important step in that direction by proving the following result (and thereby presenting an alternate solution to Question 62 in [Reference Friedman2] by providing a
![]() $\prod ^0_{2}$
singleton not arithmetically equivalent to any
$\prod ^0_{2}$
singleton not arithmetically equivalent to any
![]() ${\mathbf {0}}^{(\alpha )}$
).
${\mathbf {0}}^{(\alpha )}$
).
Corollary 4.3. There is a
![]() $\prod ^0_{2}$
singleton of minimal arithmetic degree.
$\prod ^0_{2}$
singleton of minimal arithmetic degree.
While the degrees of
![]() $\omega \text {-REA}$
sets are properly contained in the degrees of singletons, results about
$\omega \text {-REA}$
sets are properly contained in the degrees of singletons, results about
![]() $\prod ^0_{2}$
singletons have often paved the way for corresponding results about
$\prod ^0_{2}$
singletons have often paved the way for corresponding results about
![]() $\omega \text {-REA}$
sets, e.g., Harrington’s construction of an arithmetically low
$\omega \text {-REA}$
sets, e.g., Harrington’s construction of an arithmetically low
![]() $\prod ^0_{2}$
singleton [Reference Harrington5] or arithmetically incomparable
$\prod ^0_{2}$
singleton [Reference Harrington5] or arithmetically incomparable
![]() $\prod ^0_{2}$
singletons [Reference Harrington4] bothFootnote
1
foreshadowed related constructions of
$\prod ^0_{2}$
singletons [Reference Harrington4] bothFootnote
1
foreshadowed related constructions of
![]() $ \omega \text {-REA}$
sets with those properties [Reference Simpson14]. As the approach taken in this paper draws heavily on the ideas in [Reference Harrington5] we hypothesize, contra the analogy with r.e. sets, that there is an arithmetically minimal
$ \omega \text {-REA}$
sets with those properties [Reference Simpson14]. As the approach taken in this paper draws heavily on the ideas in [Reference Harrington5] we hypothesize, contra the analogy with r.e. sets, that there is an arithmetically minimal
![]() $\omega \text {-REA}$
set and hope the construction here points to a way to build such a set.
$\omega \text {-REA}$
set and hope the construction here points to a way to build such a set.
2 Background
There is a fair amount of notation required for the results in this paper; however, almost all of it is standard. Readers familiar with standard notation may wish to skip most of the subsections below and return to them only as needed for reference. However, Section 2.5 is worth looking at for all readers as it contains some slightly less common definitions and results.
2.1 Computations, strings, and degrees
We largely adopt standard notation from [Reference Odifreddi9] which we briefly review. Set difference is denoted by
![]() $X \setminus Y$
, powerset by
$X \setminus Y$
, powerset by
![]() $\mathcal {P}\left (X\right )$
, the e-th set r.e. in X is
$\mathcal {P}\left (X\right )$
, the e-th set r.e. in X is
![]() $W^{X}_{e}$
, and the e-th computable functional applied to X by
$W^{X}_{e}$
, and the e-th computable functional applied to X by
![]() $\Phi _{i}\left (X\right )$
. We denote convergence and divergence by
$\Phi _{i}\left (X\right )$
. We denote convergence and divergence by
![]() $\Phi _{i}\left (X;y\right )\downarrow $
and
$\Phi _{i}\left (X;y\right )\downarrow $
and
![]() $\Phi _{i}\left (X;y\right )\uparrow $
respectively. Convergence in s-steps is denoted by
$\Phi _{i}\left (X;y\right )\uparrow $
respectively. Convergence in s-steps is denoted by
![]() $\Phi _{i}\left (X;y\right )\downarrow _s \iff \Phi _{i,s}\left (X;y\right )\downarrow $
and its negation by
$\Phi _{i}\left (X;y\right )\downarrow _s \iff \Phi _{i,s}\left (X;y\right )\downarrow $
and its negation by ![]() .
.
We write elements of
![]() $2^{<\omega }$
and
$2^{<\omega }$
and
![]() $\omega ^{<\omega }$
(referred to as strings) like
$\omega ^{<\omega }$
(referred to as strings) like
![]() $\langle {x_0, x_1, \ldots , x_{n-1}}\rangle $
with
$\langle {x_0, x_1, \ldots , x_{n-1}}\rangle $
with
![]() ${\langle \rangle }$
denoting the empty string. For elements in
${\langle \rangle }$
denoting the empty string. For elements in
![]() $2^{<\omega }, \omega ^{<\omega }, \omega ^{\omega }, 2^{\omega }$
(identifying sets with their characteristic functions) we denote that
$2^{<\omega }, \omega ^{<\omega }, \omega ^{\omega }, 2^{\omega }$
(identifying sets with their characteristic functions) we denote that
![]() $\sigma $
is (non-strictly) extended by
$\sigma $
is (non-strictly) extended by
![]() $\tau $
by
$\tau $
by
![]() $\sigma \prec \tau $
, incompatibility by
$\sigma \prec \tau $
, incompatibility by
![]() $\mid $
, compatibility by
$\mid $
, compatibility by
![]() ${\,\not |\,}$
and use
${\,\not |\,}$
and use
![]() $<_L$
to denote the lexicographic ordering. For elements of
$<_L$
to denote the lexicographic ordering. For elements of
![]() $2^{<\omega }, \omega ^{<\omega }$
we denote the length of
$2^{<\omega }, \omega ^{<\omega }$
we denote the length of
![]() $\sigma $
by
$\sigma $
by
![]() $\lvert \sigma \rvert $
and write
$\lvert \sigma \rvert $
and write
![]() $\sigma ^{-}$
to indicate the immediate predecessor of
$\sigma ^{-}$
to indicate the immediate predecessor of
![]() $\sigma $
under
$\sigma $
under
![]() $\prec $
and write
$\prec $
and write
![]() $\alpha \widehat {\phantom {x}} \beta $
to denote
$\alpha \widehat {\phantom {x}} \beta $
to denote
![]() $\alpha $
concatenated with
$\alpha $
concatenated with
![]() $\beta $
and write
$\beta $
and write
![]() ${\langle i\rangle }^n$
to denote
${\langle i\rangle }^n$
to denote
![]() $\langle i\rangle $
concatenated with itself
$\langle i\rangle $
concatenated with itself
![]() $n \leq \omega $
times. We let
$n \leq \omega $
times. We let
![]() $\Phi _{e}\left (\sigma \right )$
denote the longest string
$\Phi _{e}\left (\sigma \right )$
denote the longest string
![]() $\tau , \lvert \tau \rvert \leq \lvert \sigma \rvert $
such that
$\tau , \lvert \tau \rvert \leq \lvert \sigma \rvert $
such that
![]() $\tau (n) = \Phi _{e,\lvert \sigma \rvert }\left (\sigma ;n\right )\downarrow $
and relativize to define
$\tau (n) = \Phi _{e,\lvert \sigma \rvert }\left (\sigma ;n\right )\downarrow $
and relativize to define
![]() $\Phi _{e}\left (\sigma \oplus X\right )$
in the obvious manner.
$\Phi _{e}\left (\sigma \oplus X\right )$
in the obvious manner.
We let
![]() $\left \ulcorner \alpha \right \urcorner $
denote the canonical bijection of
$\left \ulcorner \alpha \right \urcorner $
denote the canonical bijection of
![]() $\omega ^{< \omega }$
with
$\omega ^{< \omega }$
with
![]() $\omega $
where
$\omega $
where
![]() $\alpha \prec \beta \implies \left \ulcorner \alpha \right \urcorner < \left \ulcorner \beta \right \urcorner $
,
$\alpha \prec \beta \implies \left \ulcorner \alpha \right \urcorner < \left \ulcorner \beta \right \urcorner $
,
![]() $i < j \implies \left \ulcorner \alpha \widehat {\phantom {x}}\langle i\rangle \right \urcorner < \left \ulcorner \alpha \widehat {\phantom {x}}\langle j\rangle \right \urcorner $
, and
$i < j \implies \left \ulcorner \alpha \widehat {\phantom {x}}\langle i\rangle \right \urcorner < \left \ulcorner \alpha \widehat {\phantom {x}}\langle j\rangle \right \urcorner $
, and
![]() $\left \ulcorner {\langle \rangle }\right \urcorner = 0$
. We regularly gloss over the distinction between strings and their codes as that between sets and their characteristic functions. We let
$\left \ulcorner {\langle \rangle }\right \urcorner = 0$
. We regularly gloss over the distinction between strings and their codes as that between sets and their characteristic functions. We let
![]() $\langle x,y\rangle = \frac {1}{2}(x+y)(x+y+1)+y$
(this is a bijection of
$\langle x,y\rangle = \frac {1}{2}(x+y)(x+y+1)+y$
(this is a bijection of
![]() $\omega ^2$
with
$\omega ^2$
with
![]() $\omega $
) and we let
$\omega $
) and we let
![]() ${\left ({\langle a,b\rangle }\right )_{0}} = a$
and
${\left ({\langle a,b\rangle }\right )_{0}} = a$
and
![]() ${\left ({\langle a,b\rangle }\right )_{1}} = b$
. We define
${\left ({\langle a,b\rangle }\right )_{1}} = b$
. We define
![]() $A \oplus B$
,
$A \oplus B$
,
![]() $\oplus _{n \in S} X_n$
,
$\oplus _{n \in S} X_n$
,
![]() $ {X}^{\left [n\right ]}$
, and
$ {X}^{\left [n\right ]}$
, and
![]() ${X}^{\left [< n\right ]}$
standardly and extend these operations to strings in the obvious fashion (preserving the identification of
${X}^{\left [< n\right ]}$
standardly and extend these operations to strings in the obvious fashion (preserving the identification of
![]() $2^{\omega }$
with
$2^{\omega }$
with
![]() ${\mathcal {P}}\left (\omega \right )$
).
${\mathcal {P}}\left (\omega \right )$
).
A set X is arithmetic in Y (written
![]() $X \leq _{\mathbf {a}} Y$
) just if there is a formula in the language of arithmetic (with a designated set constant)
$X \leq _{\mathbf {a}} Y$
) just if there is a formula in the language of arithmetic (with a designated set constant)
![]() $\psi _e$
such that
$\psi _e$
such that
![]() $Y \models \psi _e(z) \iff z \in X$
(see [Reference Odifreddi9] for details). In this case we write
$Y \models \psi _e(z) \iff z \in X$
(see [Reference Odifreddi9] for details). In this case we write
![]() $\psi _e(Y) = X$
. Recall that an equivalent characterization of arithmetic reducibility is given by
$\psi _e(Y) = X$
. Recall that an equivalent characterization of arithmetic reducibility is given by
![]() $X \leq _{\mathbf {a}} Y \iff \left (\exists n \right )\!\left (X \leq _{\mathbf {T}} {{Y}^{(n)}} \right )$
. We denote the arithmetic degree of
$X \leq _{\mathbf {a}} Y \iff \left (\exists n \right )\!\left (X \leq _{\mathbf {T}} {{Y}^{(n)}} \right )$
. We denote the arithmetic degree of
![]() $\emptyset $
by
$\emptyset $
by
![]() ${\mathbf {0}}_{\mathbf {a}}$
and, as the arithmetic jump of X is defined to be
${\mathbf {0}}_{\mathbf {a}}$
and, as the arithmetic jump of X is defined to be
![]() $X^{\omega }$
, that of
$X^{\omega }$
, that of
![]() ${\mathbf {0}}^{(\omega )}$
by
${\mathbf {0}}^{(\omega )}$
by
![]() ${{\mathbf {0}}_{\mathbf {a}}}'$
. An arithmetic degree is minimal just if it has exactly one predecessor under
${{\mathbf {0}}_{\mathbf {a}}}'$
. An arithmetic degree is minimal just if it has exactly one predecessor under
![]() $\leq _{\mathbf {a}}$
.
$\leq _{\mathbf {a}}$
.
2.2 Trees and forcing
A tree T is a
![]() $\prec $
closed set of strings and
$\prec $
closed set of strings and
![]() $[T]$
is the set of paths through T. We define
$[T]$
is the set of paths through T. We define
![]() ${T^{\langle \infty \rangle }} = {\left \{{\sigma \in T}\mid {\left (\exists f \in [T] \right )\!\left (\sigma \prec f \right )}\right \}}$
and call a tree pruned if
${T^{\langle \infty \rangle }} = {\left \{{\sigma \in T}\mid {\left (\exists f \in [T] \right )\!\left (\sigma \prec f \right )}\right \}}$
and call a tree pruned if
![]() $T = {T^{\langle \infty \rangle }}$
. A node
$T = {T^{\langle \infty \rangle }}$
. A node
![]() $\sigma \in T$
is terminal if
$\sigma \in T$
is terminal if
![]() $\sigma $
has no extensions in T, branching if it has more than one immediate extension,
$\sigma $
has no extensions in T, branching if it has more than one immediate extension,
![]() $\omega $
-branching if it has infinitely many immediate extensions and the root of T if it is the unique
$\omega $
-branching if it has infinitely many immediate extensions and the root of T if it is the unique
![]() $\prec $
least branching node in T. A tree is
$\prec $
least branching node in T. A tree is
![]() $\omega $
-branching if every branching node is
$\omega $
-branching if every branching node is
![]() $\omega $
-branching. A subtree of T is a tree
$\omega $
-branching. A subtree of T is a tree
![]() $\hat {T} \subset T$
.
$\hat {T} \subset T$
.
We abuse notation and write
![]() $T{{\restriction _{l}}}$
for
$T{{\restriction _{l}}}$
for
![]() ${\left \{{\sigma \in T}\mid {\lvert \sigma \rvert \leq l}\right \}}$
. We write
${\left \{{\sigma \in T}\mid {\lvert \sigma \rvert \leq l}\right \}}$
. We write
![]() $\sigma {\mathbin {\ast }} T$
for
$\sigma {\mathbin {\ast }} T$
for
![]() ${\left \{{\sigma \widehat {\phantom {x}}\tau }\mid {\tau \in T}\right \}}$
,
${\left \{{\sigma \widehat {\phantom {x}}\tau }\mid {\tau \in T}\right \}}$
, ![]() for
for
![]() $ {\left \{{\tau }\mid {\sigma \widehat {\phantom {x}}\tau \in T}\right \}}$
(with
$ {\left \{{\tau }\mid {\sigma \widehat {\phantom {x}}\tau \in T}\right \}}$
(with ![]() the unique element of
the unique element of ![]() ) and
) and ![]() called the subtree of T above
called the subtree of T above
![]() $\sigma $
. We recall that the standard topology on
$\sigma $
. We recall that the standard topology on
![]() $\omega ^{\omega }$
is induced by basic open sets
$\omega ^{\omega }$
is induced by basic open sets
![]() $[\sigma ] = {\left \{f\mid f \succ \sigma \right \}}$
for
$[\sigma ] = {\left \{f\mid f \succ \sigma \right \}}$
for
![]() $\sigma \in \omega ^{<\omega }$
and likewise for
$\sigma \in \omega ^{<\omega }$
and likewise for
![]() $2^{\omega }$
. A set is perfect if it contains no isolated points and we call a tree T perfect if
$2^{\omega }$
. A set is perfect if it contains no isolated points and we call a tree T perfect if
![]() $[T]$
is perfect.
$[T]$
is perfect.
When working with unpruned trees in
![]() $\omega ^{<\omega }$
we can’t identify trees (
$\omega ^{<\omega }$
we can’t identify trees (
![]() $\prec $
closed sets) with
$\prec $
closed sets) with
![]() $\prec $
respecting functions on strings as we’ll do overFootnote
2
$\prec $
respecting functions on strings as we’ll do overFootnote
2
![]() $2^{<\omega }$
. We use the term f-tree for a
$2^{<\omega }$
. We use the term f-tree for a
![]() $\prec , <_L$
respecting partial function
$\prec , <_L$
respecting partial function
![]() $T{\mathop {:}{\omega ^{<\omega }}\mapsto {\omega ^{<\omega }}}$
with a
$T{\mathop {:}{\omega ^{<\omega }}\mapsto {\omega ^{<\omega }}}$
with a
![]() $\prec $
closed domain that preserves longest common initial segments, i.e.,
$\prec $
closed domain that preserves longest common initial segments, i.e.,
![]() $T(\sigma \widehat {\phantom {x}}\langle n\rangle )(\left \lvert T(\sigma )\right \rvert )$
is strictly monotonic in n (on its domain). A f-tree
$T(\sigma \widehat {\phantom {x}}\langle n\rangle )(\left \lvert T(\sigma )\right \rvert )$
is strictly monotonic in n (on its domain). A f-tree
![]() $\hat {T}$
is a subtree of an f-tree T if
$\hat {T}$
is a subtree of an f-tree T if
![]() $\mathrm {rng} \hat {T} \subset \mathrm {rng} T$
. An f-tree T is branching if every non-terminal element in
$\mathrm {rng} \hat {T} \subset \mathrm {rng} T$
. An f-tree T is branching if every non-terminal element in
![]() $\mathrm {dom} T$
has multiple immediate successors, (weakly)
$\mathrm {dom} T$
has multiple immediate successors, (weakly)
![]() $ \omega $
-branching if every non-terminal element in
$ \omega $
-branching if every non-terminal element in
![]() $\mathrm {dom} T$
has infinitely many immediate successors, and
$\mathrm {dom} T$
has infinitely many immediate successors, and
![]() $\omega $
-branching if whenever
$\omega $
-branching if whenever
![]() $\sigma \in \mathrm {dom} T$
is non-terminal than
$\sigma \in \mathrm {dom} T$
is non-terminal than
![]() $\sigma \widehat {\phantom {x}}\langle n\rangle \in \mathrm {dom} T$
for all n. Unless otherwise stated, we assume every f-tree is a branching f-tree and generalize the notions of being pruned,
$\sigma \widehat {\phantom {x}}\langle n\rangle \in \mathrm {dom} T$
for all n. Unless otherwise stated, we assume every f-tree is a branching f-tree and generalize the notions of being pruned,
![]() ${T^{\langle \infty \rangle }}$
,
${T^{\langle \infty \rangle }}$
, ![]() ,
,
![]() $\sigma {\mathbin {\ast }} T$
, and
$\sigma {\mathbin {\ast }} T$
, and
![]() $T^{\left \langle \tau \right \rangle }$
to f-trees in the obvious way.
$T^{\left \langle \tau \right \rangle }$
to f-trees in the obvious way.
We write
![]() $\sigma \Vdash \psi $
to denote forcing over
$\sigma \Vdash \psi $
to denote forcing over
![]() $2^{<\omega }$
or
$2^{<\omega }$
or
![]() $\omega ^{<\omega }$
and
$\omega ^{<\omega }$
and
![]() $\sigma \Vdash _T \psi $
to denote local forcing on the (pruned) tree T (see [Reference Odifreddi9] for details). A set/function is
$\sigma \Vdash _T \psi $
to denote local forcing on the (pruned) tree T (see [Reference Odifreddi9] for details). A set/function is
![]() $\kappa $
-generic iff it forces either
$\kappa $
-generic iff it forces either
![]() $\psi $
or
$\psi $
or
![]() $\lnot \psi $
for every
$\lnot \psi $
for every
![]() $\Sigma ^1_\lambda $
sentence with
$\Sigma ^1_\lambda $
sentence with
![]() $\lambda < 1 + \kappa $
and weakly
$\lambda < 1 + \kappa $
and weakly
![]() $\kappa $
-generic (note the application at limit ordinals) iff it meets every dense
$\kappa $
-generic (note the application at limit ordinals) iff it meets every dense
![]() $\Sigma ^1_\lambda $
set of strings. Recall that a set of strings W is dense if every string is extended by an element of W.
$\Sigma ^1_\lambda $
set of strings. Recall that a set of strings W is dense if every string is extended by an element of W.
2.3
 $ \prod ^0_{n}$
classes and
$ \prod ^0_{n}$
classes and
 $\omega $
-REA sets
$\omega $
-REA sets
A
![]() $\prod ^0_{n}$
set class is the set of elements in
$\prod ^0_{n}$
set class is the set of elements in
![]() ${\mathcal {P}}\left (\omega \right )$
(identified with
${\mathcal {P}}\left (\omega \right )$
(identified with
![]() $2^{\omega }$
) that satisfy some
$2^{\omega }$
) that satisfy some
![]() $\prod ^0_{n}$
formula with a free set variable. A
$\prod ^0_{n}$
formula with a free set variable. A
![]() $\prod ^0_{n}$
function class is defined likewise for elements in
$\prod ^0_{n}$
function class is defined likewise for elements in
![]() $\omega ^{\omega }$
. We will use the term
$\omega ^{\omega }$
. We will use the term
![]() $\prod ^0_{n}$
class without further specification to refer to a
$\prod ^0_{n}$
class without further specification to refer to a
![]() $\prod ^0_{n}$
set class. We note that if
$\prod ^0_{n}$
set class. We note that if
![]() $n> 0$
then
$n> 0$
then
![]() ${\mathscr {F} \subset \omega ^{\omega }}$
is a
${\mathscr {F} \subset \omega ^{\omega }}$
is a
![]() $\prod ^0_{n}$
function class iff there is a computable relation R and a quantifier block
$\prod ^0_{n}$
function class iff there is a computable relation R and a quantifier block
![]() $\forall x \ldots Qy$
containing n alternations such that
$\forall x \ldots Qy$
containing n alternations such that
![]() $f \in \mathscr {F}$
iff
$f \in \mathscr {F}$
iff
![]() $\forall x \ldots Qy R(f{{\restriction _{y}}}, x, \ldots , y)$
(and likewise for a
$\forall x \ldots Qy R(f{{\restriction _{y}}}, x, \ldots , y)$
(and likewise for a
![]() $\prod ^0_{n}$
set class).
$\prod ^0_{n}$
set class).
An immediate consequence of this fact is that
![]() $\prod ^0_{1}$
classes can be identified with the set of paths through a computable tree. Interestingly, up to degree,
$\prod ^0_{1}$
classes can be identified with the set of paths through a computable tree. Interestingly, up to degree,
![]() $\prod ^0_{2}$
classes and
$\prod ^0_{2}$
classes and
![]() $\prod ^0_{1}$
function classes are equivalent in the following sense.
$\prod ^0_{1}$
function classes are equivalent in the following sense.
Lemma 2.1. Every
![]() $\prod ^0_{1}$
function class is homeomorphic with a
$\prod ^0_{1}$
function class is homeomorphic with a
![]() $\prod ^0_{2}$
class via a computable (hence degree preserving) homeomorphism and vice versa. This holds with all possible uniformity.
$\prod ^0_{2}$
class via a computable (hence degree preserving) homeomorphism and vice versa. This holds with all possible uniformity.
Proof For the first claim, it is enough to note that there is a computable homeomorphism of
![]() $\omega ^{\omega }$
with
$\omega ^{\omega }$
with
![]() $2^{\omega } \setminus {\left \{{\sigma \widehat {\phantom {x}}\langle 1\rangle ^\omega }\mid {\sigma \in 2^{<\omega }}\right \}}$
given by setting
$2^{\omega } \setminus {\left \{{\sigma \widehat {\phantom {x}}\langle 1\rangle ^\omega }\mid {\sigma \in 2^{<\omega }}\right \}}$
given by setting
![]() $\Gamma (\langle \rangle ) = \langle \rangle $
and
$\Gamma (\langle \rangle ) = \langle \rangle $
and
![]() $\Gamma (\sigma \widehat {\phantom {x}}\langle i\rangle ) = \Gamma (\sigma )\widehat {\phantom {x}}\langle 1\rangle ^i\widehat {\phantom {x}}\langle 0\rangle $
.
$\Gamma (\sigma \widehat {\phantom {x}}\langle i\rangle ) = \Gamma (\sigma )\widehat {\phantom {x}}\langle 1\rangle ^i\widehat {\phantom {x}}\langle 0\rangle $
.
The other direction is slightly more tricky. Given a
![]() $\prod ^0_{2}$
class
$\prod ^0_{2}$
class
![]() $\mathscr {C}$
such that
$\mathscr {C}$
such that
![]() $X \in \mathscr {C} \iff \left (\forall z\right )\!\left (\exists y\right )\!R(X{{\restriction _{y}}}, z, y)$
define
$X \in \mathscr {C} \iff \left (\forall z\right )\!\left (\exists y\right )\!R(X{{\restriction _{y}}}, z, y)$
define
![]() $\Gamma (X)(2z)$
to be the least y such that
$\Gamma (X)(2z)$
to be the least y such that
![]() $ R(X{{\restriction _{y}}}, z, y)$
and
$ R(X{{\restriction _{y}}}, z, y)$
and
![]() $\Gamma (X)(2z+1) = X(z)$
. We now define a computable tree
$\Gamma (X)(2z+1) = X(z)$
. We now define a computable tree
![]() $T \subset \omega ^{<\omega }$
with
$T \subset \omega ^{<\omega }$
with
![]() $\mathscr {F} = [T]$
. Given
$\mathscr {F} = [T]$
. Given
![]() $\sigma \in \omega ^{<\omega }$
with
$\sigma \in \omega ^{<\omega }$
with
![]() $\lvert \sigma \rvert \equiv 0 \ \ \pmod {2}$
let
$\lvert \sigma \rvert \equiv 0 \ \ \pmod {2}$
let
![]() $\sigma = \tau \oplus \epsilon $
and place
$\sigma = \tau \oplus \epsilon $
and place
![]() $\sigma \in T$
iff
$\sigma \in T$
iff
![]() $\left (\forall l < \lvert \tau \rvert \right )\!R(\epsilon {{\restriction _{l}}}, \tau (l), l)$
. If
$\left (\forall l < \lvert \tau \rvert \right )\!R(\epsilon {{\restriction _{l}}}, \tau (l), l)$
. If
![]() $\lvert \sigma \rvert \equiv 1 \ \ \pmod {2}$
then place
$\lvert \sigma \rvert \equiv 1 \ \ \pmod {2}$
then place
![]() $\sigma \in T$
iff either
$\sigma \in T$
iff either
![]() $\sigma \widehat {\phantom {x}}\langle 0\rangle \in T$
or
$\sigma \widehat {\phantom {x}}\langle 0\rangle \in T$
or
![]() $ \sigma \widehat {\phantom {x}}\langle 1\rangle \in T$
. Clearly, T is a computable tree and
$ \sigma \widehat {\phantom {x}}\langle 1\rangle \in T$
. Clearly, T is a computable tree and
![]() $\Gamma $
is a computable continuous bijection of
$\Gamma $
is a computable continuous bijection of
![]() $\mathscr {C}$
with
$\mathscr {C}$
with
![]() $[T]$
with a continuous inverse on
$[T]$
with a continuous inverse on
![]() $[T]$
.
$[T]$
.
As the name would suggest, a
![]() $\prod ^0_{n}$
singleton is a set/function that’s the only element in a
$\prod ^0_{n}$
singleton is a set/function that’s the only element in a
![]() $\prod ^0_{n}$
class. Recall that every
$\prod ^0_{n}$
class. Recall that every
![]() $\omega \text {-REA}$
set is a
$\omega \text {-REA}$
set is a
![]() $\prod ^0_{2}$
singleton but not vice-versa. For the interested reader unfamiliar with the
$\prod ^0_{2}$
singleton but not vice-versa. For the interested reader unfamiliar with the
![]() $\omega \text {-REA}$
sets we refer them to [Reference Jockusch and Shore6] but as these sets will primarily play a motivating role in this paper it’s enough for the reader to understand that they are the result of effectively iterating the operation
$\omega \text {-REA}$
sets we refer them to [Reference Jockusch and Shore6] but as these sets will primarily play a motivating role in this paper it’s enough for the reader to understand that they are the result of effectively iterating the operation
![]() $X \mapsto X \oplus W^(X)_{i}$
$X \mapsto X \oplus W^(X)_{i}$
![]() $\omega $
many times (so the (
$\omega $
many times (so the (
![]() $n +1$
)-st component must be uniformly r.e. in the first n components).
$n +1$
)-st component must be uniformly r.e. in the first n components).
2.4 Ordinal notations
We will generalize our main theorem past
![]() $\omega $
to arbitrary ordinal notations. The reader interested in only claims about arithmetic reductions (such as the headline corollary) can assume that notations only range over
$\omega $
to arbitrary ordinal notations. The reader interested in only claims about arithmetic reductions (such as the headline corollary) can assume that notations only range over
![]() $\omega \cup {\left \{\omega \right \}}$
as the lemmas required for larger ordinal notations have been exiled to Appendix B. However, some notational conventions, inspired by [Reference Sacks12], are still necessary in either case.
$\omega \cup {\left \{\omega \right \}}$
as the lemmas required for larger ordinal notations have been exiled to Appendix B. However, some notational conventions, inspired by [Reference Sacks12], are still necessary in either case.
Kleene’s set of ordinal notations is
![]() $\mathcal {O}$
with ordering
$\mathcal {O}$
with ordering
![]() $<_{\mathcal {O}}$
. The height of
$<_{\mathcal {O}}$
. The height of
![]() $\kappa $
is
$\kappa $
is
![]() $\left \lVert \kappa \right \rVert _{\mathcal {O}}$
.
$\left \lVert \kappa \right \rVert _{\mathcal {O}}$
.
![]() $\overrightarrow {\mathcal {O}}$
is the set of limit notations,
$\overrightarrow {\mathcal {O}}$
is the set of limit notations,
![]() ${}^{+}{\mathcal {O}}$
the set of successor notations. For
${}^{+}{\mathcal {O}}$
the set of successor notations. For
![]() $ \lambda $
a limit notation we denote the n-th element of the effectively given increasing sequence defining
$ \lambda $
a limit notation we denote the n-th element of the effectively given increasing sequence defining
![]() $\lambda $
by
$\lambda $
by
![]() ${\left \{ \lambda \right \}}^{\mathcal {O}}(n)$
. We elide the differences between finite notations and elements of
${\left \{ \lambda \right \}}^{\mathcal {O}}(n)$
. We elide the differences between finite notations and elements of
![]() $ \omega $
as well as that between
$ \omega $
as well as that between
![]() $\omega $
and some canonical notation for it.
$\omega $
and some canonical notation for it.
2.5 Rates of growth
We say that
![]() $g \in \omega ^{\omega }$
is C-escaping if g isn’t dominated by any
$g \in \omega ^{\omega }$
is C-escaping if g isn’t dominated by any
![]() $f \in C$
, X-escaping for
$f \in C$
, X-escaping for
![]() $X \subset \omega $
if it escapes from
$X \subset \omega $
if it escapes from
![]() ${\left \{{f}\mid {f \equiv _{\mathbf {T}} X}\right \}}$
and arithmetically escaping if it escapes from the set of arithmetic functions. Recall that f majorizes (dominates) g iff
${\left \{{f}\mid {f \equiv _{\mathbf {T}} X}\right \}}$
and arithmetically escaping if it escapes from the set of arithmetic functions. Recall that f majorizes (dominates) g iff
![]() $f(x) \geq g(x)$
for all x (all but finitely many x). Following [Reference Odifreddi9] we draw on the fact that a Turing degree is hyperimmune just if it contains a
$f(x) \geq g(x)$
for all x (all but finitely many x). Following [Reference Odifreddi9] we draw on the fact that a Turing degree is hyperimmune just if it contains a
![]() $\mathbf {0}$
-escaping function and say that an arithmetic degree is arithmetically hyperimmune just if it contains an arithmetically escaping function. As there is no notion of a set being arithmetically hyperimmune to cause confusion, we call X arithmetically hyperimmune just if it is of arithmetically hyperimmune degree.
$\mathbf {0}$
-escaping function and say that an arithmetic degree is arithmetically hyperimmune just if it contains an arithmetically escaping function. As there is no notion of a set being arithmetically hyperimmune to cause confusion, we call X arithmetically hyperimmune just if it is of arithmetically hyperimmune degree.
It’s a well-known fact that if A is an r.e. set then A is uniformly computable in any g majorizing
![]() $m_A(x) = \min {\left \{{s}\mid {A{{\restriction _{x}}} = A_s{{\restriction _{x}}}}\right \}}$
. Thus, the degree of an r.e. set can be characterized in terms of the rate of growth of a function computable in that degree. However, it’s slightly less well-known that this isn’t just true of r.e. sets but of all
$m_A(x) = \min {\left \{{s}\mid {A{{\restriction _{x}}} = A_s{{\restriction _{x}}}}\right \}}$
. Thus, the degree of an r.e. set can be characterized in terms of the rate of growth of a function computable in that degree. However, it’s slightly less well-known that this isn’t just true of r.e. sets but of all
![]() $\prod ^0_{2}$
singletons.
$\prod ^0_{2}$
singletons.
Lemma 2.2. If f is a
![]() $\prod ^0_{1}$
function singleton then every g majorizing f uniformly computes f. If X is a
$\prod ^0_{1}$
function singleton then every g majorizing f uniformly computes f. If X is a
![]() $\prod ^0_{2}$
singleton then there is some
$\prod ^0_{2}$
singleton then there is some
![]() $f \equiv _{\mathbf {T}} X$
such that every g majorizing f uniformly computes X. Moreover, if X isn’t arithmetic then it is arithmetically hyperimmune.
$f \equiv _{\mathbf {T}} X$
such that every g majorizing f uniformly computes X. Moreover, if X isn’t arithmetic then it is arithmetically hyperimmune.
Proof By Lemma 2.1 the second and third claims follow from the first. Now suppose that f is the unique path through
![]() $[T]$
and that f is majorized by some arithmetic function g. Now let
$[T]$
and that f is majorized by some arithmetic function g. Now let
![]() $ \hat {T}$
consist of all
$ \hat {T}$
consist of all
![]() $\sigma \in T$
majorized by g (on
$\sigma \in T$
majorized by g (on
![]() $\mathrm {dom} \sigma $
). To compute
$\mathrm {dom} \sigma $
). To compute
![]() $f{{\restriction _{l}}}$
from g, search for some
$f{{\restriction _{l}}}$
from g, search for some
![]() $\sigma , k$
such that
$\sigma , k$
such that
![]() $\lvert \sigma \rvert = l$
and
$\lvert \sigma \rvert = l$
and
![]() $\left (\forall \tau \in \hat {T}\right )\!\left (\lvert \tau \rvert = k \implies \tau \succ \sigma \right )$
. As
$\left (\forall \tau \in \hat {T}\right )\!\left (\lvert \tau \rvert = k \implies \tau \succ \sigma \right )$
. As
![]() $\hat {T}$
is finitely branching and
$\hat {T}$
is finitely branching and
![]() $[\hat {T}] = {\left \{{f}\right \}}$
König’s lemma guarantees that such a k exists.
$[\hat {T}] = {\left \{{f}\right \}}$
König’s lemma guarantees that such a k exists.
3 Fast growing functions and minimality
Before we prove Corollary 4.3 we first consider a seemingly promising, but ultimately futile, approach to proving that no
![]() $\omega \text {-REA}$
set can be of minimal arithmetic degree. This failure provides an interesting result about the arithmetic degrees in its own right and illustrates both some of the similarities and differences between the role of the r.e. sets in the Turing degrees and the
$\omega \text {-REA}$
set can be of minimal arithmetic degree. This failure provides an interesting result about the arithmetic degrees in its own right and illustrates both some of the similarities and differences between the role of the r.e. sets in the Turing degrees and the
![]() $\omega \text {-REA}$
sets in the arithmetic degrees. As an added bonus it will preview some issues that will arise later and remind readers of the standard construction of a minimal arithmetic degree [Reference Sacks11].
$\omega \text {-REA}$
sets in the arithmetic degrees. As an added bonus it will preview some issues that will arise later and remind readers of the standard construction of a minimal arithmetic degree [Reference Sacks11].
3.1 Motivation
One of the most powerful methods to prove results about r.e. sets is to threaten to code one set into another (see, e.g., Sack’s proof of the Density theorem [Reference Sacks10]). However, translating this approach to the
![]() $\omega \text {-REA}$
sets under
$\omega \text {-REA}$
sets under
![]() $\leq _{\mathbf {a}}$
faces two serious barriers. First, the fact we can only place elements into the (
$\leq _{\mathbf {a}}$
faces two serious barriers. First, the fact we can only place elements into the (
![]() $n + 1$
)-th component of an
$n + 1$
)-th component of an
![]() $\omega \text {-REA}$
set if they are enumerated in an r.e. fashion from the n-th component. This makes it very difficult to threaten to code X into Y without following through. Second, the coding would somehow have to control/react to facts about arbitrarily many jumps of Y.
$\omega \text {-REA}$
set if they are enumerated in an r.e. fashion from the n-th component. This makes it very difficult to threaten to code X into Y without following through. Second, the coding would somehow have to control/react to facts about arbitrarily many jumps of Y.
One potential way to avoid these difficulties with coding is to ignore the details about what elements enter a set and just focus on rate of growth/domination. Every non-arithmetic
![]() $\prod ^0_{2}$
singleton (and hence
$\prod ^0_{2}$
singleton (and hence
![]() $ \omega \text {-REA}$
set) computes an arithmetically escaping function and we know that non-domination strength is often a good way to build sets of smaller degree, e.g., Kurtz’s proof that every hyperimmune degree computes a weak
$ \omega \text {-REA}$
set) computes an arithmetically escaping function and we know that non-domination strength is often a good way to build sets of smaller degree, e.g., Kurtz’s proof that every hyperimmune degree computes a weak
![]() $1$
-generic [Reference Kurtz7].
$1$
-generic [Reference Kurtz7].
Also, [Reference Andrews, Gerdes and Miller1] showed that every
![]() ${\mathbf {0}}'$
-escaping function computes a weak
${\mathbf {0}}'$
-escaping function computes a weak
![]() $2$
-generic (and is thus not of minimal Turing degree). While further non-domination strength won’t ensure we can compute a weak
$2$
-generic (and is thus not of minimal Turing degree). While further non-domination strength won’t ensure we can compute a weak
![]() $3$
-generic an examination of the proof of this claim [Reference Andrews, Gerdes and Miller1] suggests that this is more about the ease of avoiding genericity not necessarily a limitation on the computational power of non-domination strength. This leaves open the possibility that arithmetically escaping functions compute
$3$
-generic an examination of the proof of this claim [Reference Andrews, Gerdes and Miller1] suggests that this is more about the ease of avoiding genericity not necessarily a limitation on the computational power of non-domination strength. This leaves open the possibility that arithmetically escaping functions compute
![]() $\omega $
-generics under some local forcingFootnote
3
or other forcing notion. Besides, it simply seems intuitively unlikely that a minimal arithmetic degree, a degree which should have the very least amount of computational power, could include an arithmetically escaping function.
$\omega $
-generics under some local forcingFootnote
3
or other forcing notion. Besides, it simply seems intuitively unlikely that a minimal arithmetic degree, a degree which should have the very least amount of computational power, could include an arithmetically escaping function.
This possibility is rendered more plausible by the fact that the standard construction of a minimal arithmetic degree [Reference Sacks11] naturally produces a set which doesn’t compute any arithmetically escaping functions.
Proposition 3.1. Suppose that for every n there is an arithmetic tree
![]() $T_n \subset 2^{<\omega }$
such that
$T_n \subset 2^{<\omega }$
such that
![]() $X \in [T_n]$
and every path through
$X \in [T_n]$
and every path through
![]() $T_n$
is n-generic with respect to
$T_n$
is n-generic with respect to
![]() $\Vdash _{T_n}$
then X is arithmetically hyperimmune-free.
$\Vdash _{T_n}$
then X is arithmetically hyperimmune-free.
Proof Suppose
![]() $f \in \omega ^{\omega }$
and
$f \in \omega ^{\omega }$
and
![]() $X \models \psi (x,y) \iff f(x) = y$
for some
$X \models \psi (x,y) \iff f(x) = y$
for some
![]() $\Sigma ^1_n$
sentence
$\Sigma ^1_n$
sentence
![]() $\psi $
. We now construct an arithmetic g majorizing f as follows.
$\psi $
. We now construct an arithmetic g majorizing f as follows.
Let
![]() $m = n + 2$
and consider the sentence that asserts
$m = n + 2$
and consider the sentence that asserts
![]() $\psi (x,y)$
defines a total function
$\psi (x,y)$
defines a total function
By assumption,
![]() $X \models \varphi $
and therefore there is some
$X \models \varphi $
and therefore there is some
![]() $\sigma \prec X, \sigma \in T_m$
with
$\sigma \prec X, \sigma \in T_m$
with
![]() $\sigma \Vdash _{T_m} \varphi $
. Let
$\sigma \Vdash _{T_m} \varphi $
. Let
![]() $\hat {T}$
be the strings in
$\hat {T}$
be the strings in
![]() $T_m$
compatible with
$T_m$
compatible with
![]() $\sigma $
.
$\sigma $
.
We compute
![]() $g(x)$
by searching for a finite set of pairs
$g(x)$
by searching for a finite set of pairs
![]() $y_i, \tau _i$
with
$y_i, \tau _i$
with
![]() $\tau _i \Vdash _{T_m} \psi (x,y_i)$
such that every path through
$\tau _i \Vdash _{T_m} \psi (x,y_i)$
such that every path through
![]() $[\hat {T}]$
extends some
$[\hat {T}]$
extends some
![]() $\tau _i$
. Since all
$\tau _i$
. Since all
![]() $Y \in [\hat {T}]$
are m locally generic every such
$Y \in [\hat {T}]$
are m locally generic every such
![]() $Y \models \varphi $
. Thus, for all
$Y \models \varphi $
. Thus, for all
![]() $Y \in [\hat {T}]$
there are
$Y \in [\hat {T}]$
there are
![]() $x, y$
such that
$x, y$
such that
![]() $Y \Vdash _{T_m} \psi (x,y)$
. Thus, there is an set of pairs
$Y \Vdash _{T_m} \psi (x,y)$
. Thus, there is an set of pairs
![]() $y_i, \tau _i$
as described and the
$y_i, \tau _i$
as described and the
![]() $ \tau _i$
may be taken to be incompatible. As
$ \tau _i$
may be taken to be incompatible. As
![]() $T_m$
is finitely branching by König’s lemma, there can only be finitely many elements in
$T_m$
is finitely branching by König’s lemma, there can only be finitely many elements in
![]() $\hat {T}$
extending no
$\hat {T}$
extending no
![]() $\tau _i$
ensuring that we can always find a finite collection of such pairs. Now let
$\tau _i$
ensuring that we can always find a finite collection of such pairs. Now let
![]() $g(x)$
be larger than all the
$g(x)$
be larger than all the
![]() $y_i$
in our set of pairs.
$y_i$
in our set of pairs.
If
![]() $Y \in [\hat {T}]$
then g majorizes the function
$Y \in [\hat {T}]$
then g majorizes the function
![]() $f_Y$
where
$f_Y$
where
![]() $f_Y(x) = y \iff Y \models \psi (x,y)$
and as
$f_Y(x) = y \iff Y \models \psi (x,y)$
and as
![]() $X \in [\hat {T}]$
it follows that g majorizes f. As
$X \in [\hat {T}]$
it follows that g majorizes f. As
![]() $T_m \geq _{\mathbf {T}} \hat {T}$
is arithmetic it follows that g is an arithmetic function majorizing f.
$T_m \geq _{\mathbf {T}} \hat {T}$
is arithmetic it follows that g is an arithmetic function majorizing f.
The trees
![]() $T_n$
in the above proposition track the trees used in the construction of a minimal arithmetic degree. Thus, the usual construction of a minimal arithmetic degree produces an arithmetically hyperimmune-free degree.
$T_n$
in the above proposition track the trees used in the construction of a minimal arithmetic degree. Thus, the usual construction of a minimal arithmetic degree produces an arithmetically hyperimmune-free degree.
3.2 An arithmetically hyperimmune minimal degree
Unfortunately, despite the reasons to conjecture that arithmetically hyperimmune functions couldn’t be of minimal arithmetic degree, it turns out not to be the case. Indeed, it turns out that any amount of non-domination strength is compatible with being of minimal arithmetic degree. This contrasts with the situation in the Turing degrees where no
![]() ${\mathbf {0}}'$
escaping function can be of minimal Turing degree.
${\mathbf {0}}'$
escaping function can be of minimal Turing degree.
Theorem 3.2. There is a pruned perfect
![]() $\omega $
-branching f-tree
$\omega $
-branching f-tree
![]() $T \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
such that every
$T \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
such that every
![]() $f \in [T]$
is of minimal arithmetic degree.
$f \in [T]$
is of minimal arithmetic degree.
We will break the proof of this theorem up into a sequence of lemmas. However, before we do that let’s first verify that the theorem actually provides the desired (arguably undesired) arithmetically minimal, arithmetically hyperimmune degree.
Corollary 3.3. There is an arithmetically minimal degree
![]() $\mathbf {a}$
that is of arithmetically hyperimmune degree. Indeed, for any countable
$\mathbf {a}$
that is of arithmetically hyperimmune degree. Indeed, for any countable
![]() $C \subset \omega ^{\omega }$
there is a minimal arithmetic degree
$C \subset \omega ^{\omega }$
there is a minimal arithmetic degree
![]() $\mathbf {a}$
containing a C escaping member.
$\mathbf {a}$
containing a C escaping member.
Proof The first claim follows from the second by taking C to be the collection of arithmetic
![]() $f \in \omega ^{\omega }$
. For the second claim, fix a function h dominating every element of C and then build a path f through the tree in Theorem 3.2 by always extending
$f \in \omega ^{\omega }$
. For the second claim, fix a function h dominating every element of C and then build a path f through the tree in Theorem 3.2 by always extending
![]() $\sigma $
to
$\sigma $
to
![]() $\sigma \widehat {\phantom {x}}\langle m\rangle $
such that
$\sigma \widehat {\phantom {x}}\langle m\rangle $
such that
![]() $T(\sigma \widehat {\phantom {x}}\langle m\rangle )\downarrow $
and escapes h one more time.
$T(\sigma \widehat {\phantom {x}}\langle m\rangle )\downarrow $
and escapes h one more time.
Recall from the construction of a minimal Turing degree that
Definition 3.4. The strings
![]() $\tau _0, \tau _1$
e-split if
$\tau _0, \tau _1$
e-split if
![]() $\Phi _{e}\left (\tau _0\right ) \mid \Phi _{e}\left (\tau _1\right )$
$\Phi _{e}\left (\tau _0\right ) \mid \Phi _{e}\left (\tau _1\right )$
and that in that construction we built a sequence of computable trees
![]() $T_e \subset 2^{<\omega }$
with
$T_e \subset 2^{<\omega }$
with
![]() $T_{e+1}$
a subtree of
$T_{e+1}$
a subtree of
![]() $T_e$
such that one of the following obtains (here we identify pruned, perfect binary trees and the corresponding f-trees).
$T_e$
such that one of the following obtains (here we identify pruned, perfect binary trees and the corresponding f-trees).
-
1. (Partiality)
 $\left (\forall f \in [T_e]\right )\!\left (\Phi _{e}\left (f\right )\uparrow \right ).$
$\left (\forall f \in [T_e]\right )\!\left (\Phi _{e}\left (f\right )\uparrow \right ).$
-
2. (Non e-splitting) For all
 $\tau , \tau ' \in T_e$
,
$\tau , \tau ' \in T_e$
,
 $\tau , \tau '$
don’t e-split.
$\tau , \tau '$
don’t e-split. -
3. (e-splitting) For all
 $\sigma \in T_e$
,
$\sigma \in T_e$
,
 $T_e(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
and
$T_e(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
and
 $T_e(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
e-split.
$T_e(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
e-split.
We then build
![]() $f \in \bigcap_{e \in \omega } [T_e]$
ensuring that either
$f \in \bigcap_{e \in \omega } [T_e]$
ensuring that either
![]() $\Phi _{e}\left (f\right )$
is partial (1), computable (2), or computes f (3). We adopt the same general approach, but, to handle arithmetic reductions rather than Turing reductions we’ll replace the notion of e-splitting with an analogue based on local forcing (as in the construction of a minimal arithmetic degree from [Reference Sacks11]). We’ll then adjust this construction to allow us to build
$\Phi _{e}\left (f\right )$
is partial (1), computable (2), or computes f (3). We adopt the same general approach, but, to handle arithmetic reductions rather than Turing reductions we’ll replace the notion of e-splitting with an analogue based on local forcing (as in the construction of a minimal arithmetic degree from [Reference Sacks11]). We’ll then adjust this construction to allow us to build
![]() $\omega $
-branching trees. First, however, we introduce notation to represent an analogue of partial application of a functional for forcing.
$\omega $
-branching trees. First, however, we introduce notation to represent an analogue of partial application of a functional for forcing.
Definition 3.5. Given a notion of forcing
![]() $\Vdash $
a condition
$\Vdash $
a condition
![]() $\sigma $
and a sentence
$\sigma $
and a sentence
![]() $\psi $
with a single free (number) variable let
$\psi $
with a single free (number) variable let
![]() ${\psi ^{\Vdash }\left (\sigma \right )}$
denote the longest string
${\psi ^{\Vdash }\left (\sigma \right )}$
denote the longest string
![]() $\tau \in 2^{<\omega }$
such that
$\tau \in 2^{<\omega }$
such that
![]() $n \in \mathrm {dom} \tau $
implies
$n \in \mathrm {dom} \tau $
implies
![]() $\sigma \Vdash \psi (n) \land \tau (n) = 1$
or
$\sigma \Vdash \psi (n) \land \tau (n) = 1$
or
![]() $\sigma \Vdash \lnot \psi (n) \land \tau (n) = 0$
. We extend this in the obvious way to infinite paths.
$\sigma \Vdash \lnot \psi (n) \land \tau (n) = 0$
. We extend this in the obvious way to infinite paths.
In other words,
![]() $\psi ^{\Vdash }(\sigma )$
represents the initial segment of
$\psi ^{\Vdash }(\sigma )$
represents the initial segment of
![]() $\psi (A)$
whose values have been determined for
$\psi (A)$
whose values have been determined for
![]() $A \succ \sigma $
(assuming A is sufficiently generic).
$A \succ \sigma $
(assuming A is sufficiently generic).
Definition 3.6. If
![]() $\psi _e$
is a
$\psi _e$
is a
![]() $\Sigma ^1_n$
or
$\Sigma ^1_n$
or
![]() $\prod ^0_{n}$
formula with a single free variable then:
$\prod ^0_{n}$
formula with a single free variable then:
-
1. A pair of strings
 $\tau , \tau '$
e-fsplits on T just if
$\tau , \tau '$
e-fsplits on T just if
 ${\psi _{e}^{\Vdash _{T}}\left (\tau \right )} \mid {\psi _{e}^{\Vdash _{T}}\left (\tau \right )}$
.
${\psi _{e}^{\Vdash _{T}}\left (\tau \right )} \mid {\psi _{e}^{\Vdash _{T}}\left (\tau \right )}$
. -
2. A pruned f-tree T is totally non-e-fsplitting if there are no
 $\tau , \tau '$
in the image of T that e-fsplit.
$\tau , \tau '$
in the image of T that e-fsplit. -
3. A pruned f-tree is totally e-fsplitting if whenever
 $\sigma \in \omega ^{<\omega }, n \neq n'$
then
$\sigma \in \omega ^{<\omega }, n \neq n'$
then
 $T(\sigma \widehat {\phantom {x}}\langle n\rangle )$
,
$T(\sigma \widehat {\phantom {x}}\langle n\rangle )$
,
 $T(\sigma \widehat {\phantom {x}}\langle n'\rangle )$
e-fsplits whenever both are defined.
$T(\sigma \widehat {\phantom {x}}\langle n'\rangle )$
e-fsplits whenever both are defined. -
4. A pruned f-tree T is e-deciding if it is either totally non-e-fsplitting or totally e-fsplitting and every path through T is n generic with respect to
 $\Vdash _T$
.
$\Vdash _T$
.
Lemma 3.7. If
![]() $T:\omega ^{<\omega } \mapsto \omega ^{<\omega }$
is a pruned e-deciding f-tree,
$T:\omega ^{<\omega } \mapsto \omega ^{<\omega }$
is a pruned e-deciding f-tree,
![]() $f \in [T]$
, and
$f \in [T]$
, and
![]() ${X = \psi _e(f)}$
then X is either arithmetic in T or f is arithmetic in
${X = \psi _e(f)}$
then X is either arithmetic in T or f is arithmetic in
![]() $X \oplus T$
.
$X \oplus T$
.
Proof As every path through T is n-generic with respect to
![]() $\Vdash _{T}$
if
$\Vdash _{T}$
if
![]() $f \Vdash _{T} \psi _e(x)$
then
$f \Vdash _{T} \psi _e(x)$
then
![]() $x \in \psi _e(f)$
. Hence, if T is totally non-e-fsplitting then (the characteristic function for) X is the union of
$x \in \psi _e(f)$
. Hence, if T is totally non-e-fsplitting then (the characteristic function for) X is the union of
![]() ${\psi _{e}^{\Vdash _{T}}\left (\tau \right )}$
for
${\psi _{e}^{\Vdash _{T}}\left (\tau \right )}$
for
![]() $\tau $
in the image of T. If T is totally e-fsplitting and
$\tau $
in the image of T. If T is totally e-fsplitting and
![]() $X = \psi _e(f)$
then f is the union of
$X = \psi _e(f)$
then f is the union of
![]() $\tau $
in the image of T with
$\tau $
in the image of T with
![]() $ {\psi _{e}^{\Vdash _{T}}\left (\tau \right )}$
compatible with X. As forcing for arithmetic sentences is arithmetic the conclusion follows.
$ {\psi _{e}^{\Vdash _{T}}\left (\tau \right )}$
compatible with X. As forcing for arithmetic sentences is arithmetic the conclusion follows.
We now prove the key lemma we’ll use to establish Theorem 3.2.
Lemma 3.8. Given e and a pruned
![]() $\omega $
-branching perfect f-tree
$\omega $
-branching perfect f-tree
![]() $T\!: \omega ^{<\omega } \mapsto \omega ^{<\omega }$
there is a pruned
$T\!: \omega ^{<\omega } \mapsto \omega ^{<\omega }$
there is a pruned
![]() $\omega $
-branching perfect e-deciding subtree
$\omega $
-branching perfect e-deciding subtree
![]() $\hat {T}$
uniformly arithmetic in T.
$\hat {T}$
uniformly arithmetic in T.
Proof We first observe that given a pruned perfect f-tree T there is a pruned perfect subtree
![]() $\tilde {T}$
where every path through
$\tilde {T}$
where every path through
![]() $\tilde {T}$
is n-generic with respect to
$\tilde {T}$
is n-generic with respect to
![]() $\Vdash _{T}$
. Moreover, we note that since
$\Vdash _{T}$
. Moreover, we note that since
![]() $\sigma \Vdash _{T} \psi \implies \sigma \Vdash _{\tilde {T}} \psi $
every path is also n-generic with respect to
$\sigma \Vdash _{T} \psi \implies \sigma \Vdash _{\tilde {T}} \psi $
every path is also n-generic with respect to
![]() $\tilde {T}$
and if T was either totally non-e-fsplitting or totally e-fsplitting and
$\tilde {T}$
and if T was either totally non-e-fsplitting or totally e-fsplitting and
![]() $\psi _e \in \Sigma ^1_n \cup \prod ^0_{n}$
than
$\psi _e \in \Sigma ^1_n \cup \prod ^0_{n}$
than
![]() $\tilde {T}$
is e-deciding. As we can take
$\tilde {T}$
is e-deciding. As we can take
![]() $\tilde {T}$
to be arithmetic in T, it is enough to demonstrate that there is pruned
$\tilde {T}$
to be arithmetic in T, it is enough to demonstrate that there is pruned
![]() $\omega $
-branching perfect subtree of
$\omega $
-branching perfect subtree of
![]() $ T$
,
$ T$
,
![]() $\hat {T}$
arithmetic in T that is either totally non-e-fsplitting or totally e-fsplitting.
$\hat {T}$
arithmetic in T that is either totally non-e-fsplitting or totally e-fsplitting.
We consider two cases.
Case 1: Suppose some
![]() $\sigma \in \mathrm {rng} T$
isn’t extended by any e-fsplit
$\sigma \in \mathrm {rng} T$
isn’t extended by any e-fsplit
![]() $\tau _0, \tau _1 \in \mathrm {rng} T$
. Let
$\tau _0, \tau _1 \in \mathrm {rng} T$
. Let
![]() $\hat {T} = T^{\left \langle \sigma \right \rangle }$
, the subtree of T above
$\hat {T} = T^{\left \langle \sigma \right \rangle }$
, the subtree of T above
![]() $\sigma $
. Clearly,
$\sigma $
. Clearly,
![]() $\hat {T}$
is totally non-e-fsplitting.
$\hat {T}$
is totally non-e-fsplitting.
Case 2: Suppose Case 1 doesn’t hold. We now seek to build a perfect pruned
![]() $\omega $
-branching totally e-fsplitting subtree
$\omega $
-branching totally e-fsplitting subtree
![]() $\hat {T}$
of T. Absent the need to be
$\hat {T}$
of T. Absent the need to be
![]() $ \omega $
branching we could simply search for an e-fsplitting pair extending
$ \omega $
branching we could simply search for an e-fsplitting pair extending
![]() $\hat {T}(\sigma )$
on T to define
$\hat {T}(\sigma )$
on T to define
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle ), \hat {T}(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
. However, if we then later tried to define
$\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle ), \hat {T}(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
. However, if we then later tried to define
![]() $ \hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
we might be unable to choose a value for
$ \hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
we might be unable to choose a value for
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
which e-fsplits with
$\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
which e-fsplits with
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
. We could further extend
$\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
. We could further extend
![]() $T(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
to find a splitting but we risk having to do this infinitely often. Instead, we make sure that when we pick a value for
$T(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
to find a splitting but we risk having to do this infinitely often. Instead, we make sure that when we pick a value for
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
it e-fsplits with extensions of infinitely many other strings of the form
$\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
it e-fsplits with extensions of infinitely many other strings of the form
![]() $ \hat {T}(\sigma )\widehat {\phantom {x}}\langle i\rangle $
.
$ \hat {T}(\sigma )\widehat {\phantom {x}}\langle i\rangle $
.
To define
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
we essentially repeat the above process and choose one of the infinitely many extensions which e-fsplits with
$\hat {T}(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
we essentially repeat the above process and choose one of the infinitely many extensions which e-fsplits with
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
that can be extended to e-fsplit with (extensions of) an infinite subset of those allowed extensions. The seemingly daunting details spelled out below are just the bookkeeping needed to allow us to repeatedly select a value for
$\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
that can be extended to e-fsplit with (extensions of) an infinite subset of those allowed extensions. The seemingly daunting details spelled out below are just the bookkeeping needed to allow us to repeatedly select a value for
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
and ensure that we have an infinite set of options that e-fsplit with
$\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
and ensure that we have an infinite set of options that e-fsplit with
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle i'\rangle ), i' \leq i$
to use for
$\hat {T}(\sigma \widehat {\phantom {x}}\langle i'\rangle ), i' \leq i$
to use for
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle i'\rangle ), i'> i$
(and to do this for every
$\hat {T}(\sigma \widehat {\phantom {x}}\langle i'\rangle ), i'> i$
(and to do this for every
![]() $\sigma $
).
$\sigma $
).
We build an f-tree
![]() $V\!: \omega ^{<\omega } \mapsto \omega ^{<\omega }$
and define
$V\!: \omega ^{<\omega } \mapsto \omega ^{<\omega }$
and define
![]() $\hat {T} = T \mathbin {\circ } V$
. Our construction of V will proceed in stages. At stage s we will define
$\hat {T} = T \mathbin {\circ } V$
. Our construction of V will proceed in stages. At stage s we will define
![]() $V(\sigma )$
where
$V(\sigma )$
where
![]() $s = \left \ulcorner \sigma \right \urcorner $
(remember, that
$s = \left \ulcorner \sigma \right \urcorner $
(remember, that
![]() $\sigma \prec \tau \implies \left \ulcorner \sigma \right \urcorner < \left \ulcorner \tau \right \urcorner $
). At stage
$\sigma \prec \tau \implies \left \ulcorner \sigma \right \urcorner < \left \ulcorner \tau \right \urcorner $
). At stage
![]() $0 = \left \ulcorner \langle \rangle \right \urcorner $
we begin by defining
$0 = \left \ulcorner \langle \rangle \right \urcorner $
we begin by defining
![]() $V(\langle \rangle ) = \langle \rangle $
. Note that, since
$V(\langle \rangle ) = \langle \rangle $
. Note that, since
![]() $i < j \implies \left \ulcorner \sigma \widehat {\phantom {x}}\langle i\rangle \right \urcorner < \left \ulcorner \sigma \widehat {\phantom {x}}\langle j\rangle \right \urcorner $
if
$i < j \implies \left \ulcorner \sigma \widehat {\phantom {x}}\langle i\rangle \right \urcorner < \left \ulcorner \sigma \widehat {\phantom {x}}\langle j\rangle \right \urcorner $
if
![]() $\left \ulcorner \sigma \widehat {\phantom {x}}\langle n\rangle \right \urcorner = s$
then we’ve already defined
$\left \ulcorner \sigma \widehat {\phantom {x}}\langle n\rangle \right \urcorner = s$
then we’ve already defined
![]() $V(\sigma \widehat {\phantom {x}}\langle m\rangle ), m < n$
.
$V(\sigma \widehat {\phantom {x}}\langle m\rangle ), m < n$
.
Once we’ve defined
![]() $V(\sigma )$
we maintain a set
$V(\sigma )$
we maintain a set
![]() $S^{\sigma }_s$
of extensions of
$S^{\sigma }_s$
of extensions of
![]() $\sigma $
representing possible initial segments of
$\sigma $
representing possible initial segments of
![]() $V(\sigma \widehat {\phantom {x}}\langle i\rangle )$
for
$V(\sigma \widehat {\phantom {x}}\langle i\rangle )$
for
![]() $V(\sigma \widehat {\phantom {x}}\langle i\rangle )$
not yet defined at s. To ensure that
$V(\sigma \widehat {\phantom {x}}\langle i\rangle )$
not yet defined at s. To ensure that
![]() $\hat {T}$
remains
$\hat {T}$
remains
![]() $\omega $
-branching we ensure that all elements in
$\omega $
-branching we ensure that all elements in
![]() $S^{\sigma }_s$
extend incompatible immediate extensions of
$S^{\sigma }_s$
extend incompatible immediate extensions of
![]() $\sigma $
. Unless otherwise specified,
$\sigma $
. Unless otherwise specified,
![]() $S^{\sigma }_{s+1} = S^{\sigma }_s$
.
$S^{\sigma }_{s+1} = S^{\sigma }_s$
.
Suppose that at stage s we are working to define
![]() $V(\sigma \widehat {\phantom {x}}\langle n\rangle )$
, i.e.,
$V(\sigma \widehat {\phantom {x}}\langle n\rangle )$
, i.e.,
![]() $\left \ulcorner \sigma \widehat {\phantom {x}}\langle n\rangle \right \urcorner = s$
. Let
$\left \ulcorner \sigma \widehat {\phantom {x}}\langle n\rangle \right \urcorner = s$
. Let
![]() $\tau $
be the lexicographically least element of
$\tau $
be the lexicographically least element of
![]() $S^{\sigma }_s$
and
$S^{\sigma }_s$
and
![]() $U = S^{\sigma }_s \setminus {\left \{\tau \right \}}$
. Let
$U = S^{\sigma }_s \setminus {\left \{\tau \right \}}$
. Let
![]() $\tau _0, \tau _1 \succ \tau $
be such that
$\tau _0, \tau _1 \succ \tau $
be such that
![]() $T(\tau _0), T(\tau _1)$
e-fsplit. Such strings must exist or Case 1 would have obtained. Let
$T(\tau _0), T(\tau _1)$
e-fsplit. Such strings must exist or Case 1 would have obtained. Let
![]() $U_i, i \in {\left \{0,1\right \}}$
be the set of
$U_i, i \in {\left \{0,1\right \}}$
be the set of
![]() $\prec $
minimal
$\prec $
minimal
![]() $\upsilon $
extending some element in U such that
$\upsilon $
extending some element in U such that
![]() $T(\upsilon )$
and
$T(\upsilon )$
and
![]() $T(\tau _i)$
e-fsplit. Let
$T(\tau _i)$
e-fsplit. Let
![]() $i \in {\left \{0,1\right \}}$
by the least such that
$i \in {\left \{0,1\right \}}$
by the least such that
![]() $U_i$
is infinite. Since the ‘images’ of
$U_i$
is infinite. Since the ‘images’ of
![]() $T(\tau _0)$
and
$T(\tau _0)$
and
![]() $T(\tau _1)$
under
$T(\tau _1)$
under
![]() $\psi _e$
disagree such an i must exist.
$\psi _e$
disagree such an i must exist.
Set
![]() $V(\sigma \widehat {\phantom {x}}\langle n\rangle ) = \tau _i$
and
$V(\sigma \widehat {\phantom {x}}\langle n\rangle ) = \tau _i$
and
![]() $S^{\sigma }_{s+1} = U_i$
, initialize
$S^{\sigma }_{s+1} = U_i$
, initialize
![]() $S^{\sigma \widehat {\phantom {x}}\langle n\rangle }$
to
$S^{\sigma \widehat {\phantom {x}}\langle n\rangle }$
to
![]() ${\left \{{\tau _i\widehat {\phantom {x}}\langle m\rangle }\mid {m \in \omega }\right \}}$
, and proceed to stage
${\left \{{\tau _i\widehat {\phantom {x}}\langle m\rangle }\mid {m \in \omega }\right \}}$
, and proceed to stage
![]() $s + 1$
. This completes our definition of V and clearly defines a pruned f-tree
$s + 1$
. This completes our definition of V and clearly defines a pruned f-tree
![]() $\hat {T} = T \circ V$
arithmetically in T.
$\hat {T} = T \circ V$
arithmetically in T.
We claim that
![]() $\hat {T}$
is a totally e-fsplitting perfect
$\hat {T}$
is a totally e-fsplitting perfect
![]() $\omega $
-branching subtree of T. Our definition of
$\omega $
-branching subtree of T. Our definition of
![]() $S^{\sigma }_s$
ensures that
$S^{\sigma }_s$
ensures that
![]() $\hat {T}$
is
$\hat {T}$
is
![]() $\omega $
-branching and that
$\omega $
-branching and that
![]() $\hat {T}$
is perfect. Since whenever we define
$\hat {T}$
is perfect. Since whenever we define
![]() $V(\sigma \widehat {\phantom {x}}\langle n\rangle )$
we limit
$V(\sigma \widehat {\phantom {x}}\langle n\rangle )$
we limit
![]() $T(V(\sigma \widehat {\phantom {x}}\langle n'\rangle )), n'> n$
to extensions of strings which e-fsplit with
$T(V(\sigma \widehat {\phantom {x}}\langle n'\rangle )), n'> n$
to extensions of strings which e-fsplit with
![]() $T(V(\sigma \widehat {\phantom {x}}\langle n\rangle ))$
it follows that
$T(V(\sigma \widehat {\phantom {x}}\langle n\rangle ))$
it follows that
![]() $\hat {T}$
is totally e-fsplitting.
$\hat {T}$
is totally e-fsplitting.
As these cases are exhaustive, this suffices to complete the proof.
We can now complete the proof of the theorem.
Theorem 3.2. There is a pruned perfect
![]() $\omega $
-branching f-tree
$\omega $
-branching f-tree
![]() $T \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
such that every
$T \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
such that every
![]() $f \in [T]$
is of minimal arithmetic degree.
$f \in [T]$
is of minimal arithmetic degree.
Proof Iteratively applying Lemma 3.8 would immediately suffice to produce a minimal arithmetic degree. However, we wish to end up with an
![]() $\omega $
-branching tree of such degrees. To that end, we set
$\omega $
-branching tree of such degrees. To that end, we set
![]() $ T_{0}$
to be the identity function on
$ T_{0}$
to be the identity function on
![]() $\omega ^{<\omega }$
and inductively define
$\omega ^{<\omega }$
and inductively define
![]() $T_{n+1}{{\restriction _{n}}} = T_n{{\restriction _{n}}}$
(i.e., equal when applied to strings of length at most n) and if
$T_{n+1}{{\restriction _{n}}} = T_n{{\restriction _{n}}}$
(i.e., equal when applied to strings of length at most n) and if
![]() $\lvert \sigma \rvert = n$
and
$\lvert \sigma \rvert = n$
and
![]() $T^{\sigma }_{n+1}$
is the n -deciding subtree of
$T^{\sigma }_{n+1}$
is the n -deciding subtree of
![]() $T_n^{\left \langle T_n(\sigma ) \right \rangle }$
produced by Lemma 3.8 then
$T_n^{\left \langle T_n(\sigma ) \right \rangle }$
produced by Lemma 3.8 then
![]() $T_{n+1}(\sigma \widehat {\phantom {x}}\tau ) = T_n(\sigma ) {\mathbin {\ast }} T^{\sigma }_{n+1}$
.
$T_{n+1}(\sigma \widehat {\phantom {x}}\tau ) = T_n(\sigma ) {\mathbin {\ast }} T^{\sigma }_{n+1}$
.
Now let T be the limit of this process, i.e.,
![]() $T(\sigma ) = T_{\lvert \sigma \rvert }(\sigma )$
. T is a perfect pruned
$T(\sigma ) = T_{\lvert \sigma \rvert }(\sigma )$
. T is a perfect pruned
![]() $\omega $
-branching f-tree. Since we defined
$\omega $
-branching f-tree. Since we defined
![]() $T_{n+1}$
in a uniform arithmetic fashion from
$T_{n+1}$
in a uniform arithmetic fashion from
![]() $T_n$
we have
$T_n$
we have
![]() $T \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
. Finally, if
$T \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
. Finally, if
![]() $f \in [T]$
and
$f \in [T]$
and
![]() $X = \psi _e(f)$
and
$X = \psi _e(f)$
and
![]() $\sigma = f{{\restriction _{e+1}}}$
then
$\sigma = f{{\restriction _{e+1}}}$
then ![]() and thus, as
and thus, as
![]() $T^{\sigma }_{e+1}$
is arithmetic, by Lemma 3.7 either X is arithmetic or
$T^{\sigma }_{e+1}$
is arithmetic, by Lemma 3.7 either X is arithmetic or ![]() is arithmetic in X.
is arithmetic in X.
3.3 Fast growth and definability
In retrospect, perhaps we shouldn’t be too surprised by the result in the last section. After all, there are minimal Turing degrees of hyperimmune degree (e.g., any minimal degree below
![]() ${\mathbf {0}}'$
). And maybe we don’t have to completely give up the idea of using non-domination strength to show that no
${\mathbf {0}}'$
). And maybe we don’t have to completely give up the idea of using non-domination strength to show that no
![]() $\omega \text {-REA}$
set can be of minimal arithmetic degree. While, surprisingly, unlike a true
$\omega \text {-REA}$
set can be of minimal arithmetic degree. While, surprisingly, unlike a true
![]() $1$
-generic, a weak
$1$
-generic, a weak
![]() $1$
-generic can be of minimal Turing degree (a minimal degree below
$1$
-generic can be of minimal Turing degree (a minimal degree below
![]() ${\mathbf {0}}'$
can’t be hyperimmune-free and thus computes a weak
${\mathbf {0}}'$
can’t be hyperimmune-free and thus computes a weak
![]() $1$
-generic which, by virtue of being non-computable, must be of that very minimal degree), we were still able to use non-domination strength to demonstrate the non-existence of minimal r.e. degrees by identifying a property (weak
$1$
-generic which, by virtue of being non-computable, must be of that very minimal degree), we were still able to use non-domination strength to demonstrate the non-existence of minimal r.e. degrees by identifying a property (weak
![]() $1$
-genericity) that enough non-domination strength would let us satisfy (compute) but which couldn’t hold of any set of r.e. degree. Perhaps we could similarly show that every arithmetically escaping function computes a non-arithmetic set with a property that guarantees it’s not of
$1$
-genericity) that enough non-domination strength would let us satisfy (compute) but which couldn’t hold of any set of r.e. degree. Perhaps we could similarly show that every arithmetically escaping function computes a non-arithmetic set with a property that guarantees it’s not of
![]() $\omega \text {-REA}$
degree.
$\omega \text {-REA}$
degree.
What might play the role of this property in the arithmetic degrees? The result in [Reference Andrews, Gerdes and Miller1] tells us that it can’t be
![]() $\omega $
-genericity but the following lemma suggests a different way of generalizing the idea that more non-domination strength should somehow allow us to compute less definable sets.
$\omega $
-genericity but the following lemma suggests a different way of generalizing the idea that more non-domination strength should somehow allow us to compute less definable sets.
Lemma 3.9. If
![]() $X \subset \omega $
is n-generic with respect to local forcing on some perfect tree (or weakly n-generic) then X isn’t a
$X \subset \omega $
is n-generic with respect to local forcing on some perfect tree (or weakly n-generic) then X isn’t a
![]() $\prod ^0_{n}$
singleton. Similarly, no n-generic
$\prod ^0_{n}$
singleton. Similarly, no n-generic
![]() $f \in \omega ^{\omega }$
is a
$f \in \omega ^{\omega }$
is a
![]() $\prod ^0_{n}$
function singleton.
$\prod ^0_{n}$
function singleton.
Proof Suppose that X is the unique set such that
![]() $X \models \psi $
for some
$X \models \psi $
for some
![]() $\prod ^0_{n}$
formula (with a set constant)
$\prod ^0_{n}$
formula (with a set constant)
![]() $\psi $
. By n-genericity we must have
$\psi $
. By n-genericity we must have
![]() $X{{\restriction _{l}}} \Vdash _{T} \psi $
for some l. As T is perfect there is some n-generic path
$X{{\restriction _{l}}} \Vdash _{T} \psi $
for some l. As T is perfect there is some n-generic path
![]() $Y \succ X{{\restriction _{l}}}, Y \neq X$
through T. But, by n-genericity
$Y \succ X{{\restriction _{l}}}, Y \neq X$
through T. But, by n-genericity
![]() $Y \models \psi $
contradicting the fact that X was the unique solution.
$Y \models \psi $
contradicting the fact that X was the unique solution.
To show the claim holds for weakly n-generic sets suppose that
![]() $\psi = \left (\forall x\right )\! \Psi (x)$
. Now let
$\psi = \left (\forall x\right )\! \Psi (x)$
. Now let
![]() $S = {\left \{{\sigma }\mid {\left (\exists x\right )\!\left ( \sigma \Vdash \lnot \Psi (x) \right )}\right \}}$
. S is a
$S = {\left \{{\sigma }\mid {\left (\exists x\right )\!\left ( \sigma \Vdash \lnot \Psi (x) \right )}\right \}}$
. S is a
![]() $\Sigma ^1_n$
set and if no element in S extended
$\Sigma ^1_n$
set and if no element in S extended
![]() $\tau $
then
$\tau $
then
![]() $\tau \Vdash ^{w} \psi $
and, as above, would contradict the uniqueness of X. Hence, S is a
$\tau \Vdash ^{w} \psi $
and, as above, would contradict the uniqueness of X. Hence, S is a
![]() $\Sigma ^1_n$
dense set of strings and, as every weak n generic is (
$\Sigma ^1_n$
dense set of strings and, as every weak n generic is (
![]() $n - 1$
)-generic and
$n - 1$
)-generic and
![]() $\lnot \Psi \in \prod ^0_{n - 1}$
, if X is a weak n-generic meeting S then
$\lnot \Psi \in \prod ^0_{n - 1}$
, if X is a weak n-generic meeting S then
![]() $X \models \lnot \psi $
.
$X \models \lnot \psi $
.
The argument for function singletons proceeds identically.
In this light, we can think of the results from [Reference Andrews, Gerdes and Miller1] as showing us that any
![]() $\mathbf {0}$
-escaping function computes a set that’s not a
$\mathbf {0}$
-escaping function computes a set that’s not a
![]() $\prod ^0_{1}$
singleton and any
$\prod ^0_{1}$
singleton and any
![]() ${\mathbf {0}}'$
-escaping function computes a set that’s not a
${\mathbf {0}}'$
-escaping function computes a set that’s not a
![]() $\prod ^0_{2}$
singleton.Footnote
4
We leave it as an exercise to demonstrate that the techniques in [Reference Andrews, Gerdes and Miller1] show that sufficient non-domination strength allows us to compute a set that’s not a
$\prod ^0_{2}$
singleton.Footnote
4
We leave it as an exercise to demonstrate that the techniques in [Reference Andrews, Gerdes and Miller1] show that sufficient non-domination strength allows us to compute a set that’s not a
![]() $\prod ^0_{3}$
singleton. Thus, a plausible conjecture is that an arithmetically escaping function computes a set that’s not an arithmetic singleton (i.e., not a
$\prod ^0_{3}$
singleton. Thus, a plausible conjecture is that an arithmetically escaping function computes a set that’s not an arithmetic singleton (i.e., not a
![]() $\prod ^0_{n}$
singleton for any n). If true, this would prove that no
$\prod ^0_{n}$
singleton for any n). If true, this would prove that no
![]() $\omega \text {-REA}$
set is on minimal arithmetic degree.
$\omega \text {-REA}$
set is on minimal arithmetic degree.
Proposition 3.10. If every arithmetically escaping function f can arithmetically define a set that’s not an arithmetic singleton then no
![]() $\prod ^0_{2}$
singleton, and hence no
$\prod ^0_{2}$
singleton, and hence no
![]() $\omega \text {-REA}$
set, is of minimal arithmetic degree.
$\omega \text {-REA}$
set, is of minimal arithmetic degree.
Proof Suppose, for contradiction, X is a
![]() $\prod ^0_{2}$
singleton of minimal arithmetic degree. By Lemma 2.2 X computes an arithmetically escaping f. Let
$\prod ^0_{2}$
singleton of minimal arithmetic degree. By Lemma 2.2 X computes an arithmetically escaping f. Let
![]() $Y \leq _{\mathbf {a}} f$
such that Y isn’t an arithmetic singleton as per the proposition. If Y were arithmetic then Y would be a
$Y \leq _{\mathbf {a}} f$
such that Y isn’t an arithmetic singleton as per the proposition. If Y were arithmetic then Y would be a
![]() $\Sigma ^1_n$
set for some n and thus an arithmetic singleton. Therefore, we must have
$\Sigma ^1_n$
set for some n and thus an arithmetic singleton. Therefore, we must have
![]() $Y \equiv _{\mathbf {a}} X$
. Thus, for some arithmetic formulas
$Y \equiv _{\mathbf {a}} X$
. Thus, for some arithmetic formulas
![]() $\psi , \Psi $
we have
$\psi , \Psi $
we have
![]() $\psi (X) = Y \land \Psi (Y) = X$
and thus Y is the unique solution of the arithmetic formula which asserts that
$\psi (X) = Y \land \Psi (Y) = X$
and thus Y is the unique solution of the arithmetic formula which asserts that
![]() $\Psi (Y)$
satisfies the
$\Psi (Y)$
satisfies the
![]() $\prod ^0_{2}$
formula defining X and that
$\prod ^0_{2}$
formula defining X and that
![]() $\psi (\Psi (Y)) = Y$
. Contradiction.
$\psi (\Psi (Y)) = Y$
. Contradiction.
4 An arithmetically minimal
 $ \prod ^0_{2}$
singleton
$ \prod ^0_{2}$
singleton
We will now prove that our seemingly plausible conjectures (once again) fail and that there is a
![]() $\prod ^0_{2}$
singleton of minimal arithmetic degree. Our approach to proving this borrows substantially from Harrington’s proof of McLaughlin’s conjecture [Reference Harrington5]. As it’s easier to work with computable trees than
$\prod ^0_{2}$
singleton of minimal arithmetic degree. Our approach to proving this borrows substantially from Harrington’s proof of McLaughlin’s conjecture [Reference Harrington5]. As it’s easier to work with computable trees than
![]() $\prod ^0_{2}$
classes we’ll work in
$\prod ^0_{2}$
classes we’ll work in
![]() $\omega ^{<\omega }$
. By Lemma 2.1 it will be enough to build a computable tree
$\omega ^{<\omega }$
. By Lemma 2.1 it will be enough to build a computable tree
![]() $T \subset \omega ^{<\omega }$
with a single path f of minimal arithmetic degree. However, doing this in a single step would be dauntingly difficult, so we instead break up our construction into steps.
$T \subset \omega ^{<\omega }$
with a single path f of minimal arithmetic degree. However, doing this in a single step would be dauntingly difficult, so we instead break up our construction into steps.
Specifically, the primary task will be to prove the following proposition.
Proposition 4.1. Given a (potentially partial) tree
![]() $S \subset \omega ^{<\omega }$
computable in
$S \subset \omega ^{<\omega }$
computable in
![]() ${X}^{\prime \prime }$
there is a (total) computable tree
${X}^{\prime \prime }$
there is a (total) computable tree
![]() $T \subset \omega ^{<\omega }$
and an
$T \subset \omega ^{<\omega }$
and an
![]() ${X}^{\prime \prime }$
computable partial f-tree
${X}^{\prime \prime }$
computable partial f-tree
![]() $\hat {T}$
such that:
$\hat {T}$
such that:
-
1.
 $\mathrm {rng} \hat {T} \subset T$
and
$\mathrm {rng} \hat {T} \subset T$
and
 $[\hat {T}] = [T]$
.
$[\hat {T}] = [T]$
. -
2.
 $\hat {T}(\cdot )$
is a homeomorphism of
$\hat {T}(\cdot )$
is a homeomorphism of
 $[S]$
with
$[S]$
with
 $[T]$
.
$[T]$
. -
3. If
 $f \in [T]$
then
$f \in [T]$
then
 $f \nleq _{\mathbf {T}} X$
.
$f \nleq _{\mathbf {T}} X$
. -
4. If
 $g \in [S]$
then
$g \in [S]$
then
 $g \oplus {X}^{\prime \prime } \equiv _{\mathbf {T}} {\left (\hat {T}(g) \oplus X\right )}^{\prime \prime } \equiv _{\mathbf {T}} \hat {T}(g) \oplus {X}^{\prime \prime }$
.
$g \oplus {X}^{\prime \prime } \equiv _{\mathbf {T}} {\left (\hat {T}(g) \oplus X\right )}^{\prime \prime } \equiv _{\mathbf {T}} \hat {T}(g) \oplus {X}^{\prime \prime }$
. -
5. If
 $f \in [T]$
and
$f \in [T]$
and
 $Y \leq _{\mathbf {T}} f \oplus X$
then either
$Y \leq _{\mathbf {T}} f \oplus X$
then either
 $Y \leq _{\mathbf {T}} X$
or
$Y \leq _{\mathbf {T}} X$
or
 $f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
.
$f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
. -
6. For all
 $\sigma \in 2^{<\omega }$
,
$\sigma \in 2^{<\omega }$
,
 $\left \lvert \hat {T}(\sigma )\right \rvert \geq \lvert \sigma \rvert $
(when defined).
$\left \lvert \hat {T}(\sigma )\right \rvert \geq \lvert \sigma \rvert $
(when defined).
Moreover, this holds with all possible uniformity. In particular, given a computable functional
![]() $\Upsilon _2$
we can effectively produce functionals
$\Upsilon _2$
we can effectively produce functionals
![]() $\Upsilon , \hat {\Upsilon }$
so that whenever
$\Upsilon , \hat {\Upsilon }$
so that whenever
![]() ${\Upsilon _2({X}^{\prime \prime }) =S}$
then
${\Upsilon _2({X}^{\prime \prime }) =S}$
then
![]() $\Upsilon (X)=T$
and
$\Upsilon (X)=T$
and
![]() $\hat {\Upsilon }({X}^{\prime \prime }) = \hat {T}$
with the properties described above.
$\hat {\Upsilon }({X}^{\prime \prime }) = \hat {T}$
with the properties described above.
We will then leverage this proposition to prove the main theorem below by using it repeatedly to pull down a tree
![]() $T_\alpha \leq _{\mathbf {T}} {\mathbf {0}}^{(\alpha )}$
to a homeomorphic image
$T_\alpha \leq _{\mathbf {T}} {\mathbf {0}}^{(\alpha )}$
to a homeomorphic image
![]() $T \leq _{\mathbf {T}} \mathbf {0}$
.
$T \leq _{\mathbf {T}} \mathbf {0}$
.
Theorem 4.2. Given a limit ordinal
![]() $\alpha < {\omega ^{\text {CK}}_1}$
and a tree
$\alpha < {\omega ^{\text {CK}}_1}$
and a tree
![]() $T_{\alpha } \subset \omega ^{<\omega }, T_\alpha \leq _{\mathbf {T}} {\mathbf {0}}^{(\alpha )}$
there is a computable tree T and an f-tree
$T_{\alpha } \subset \omega ^{<\omega }, T_\alpha \leq _{\mathbf {T}} {\mathbf {0}}^{(\alpha )}$
there is a computable tree T and an f-tree
![]() $\Gamma \leq _{\mathbf {T}} {\mathbf {0}}^{(\alpha )}$
such that
$\Gamma \leq _{\mathbf {T}} {\mathbf {0}}^{(\alpha )}$
such that
![]() $\Gamma $
is a homeomorphism of
$\Gamma $
is a homeomorphism of
![]() $[T_\alpha ]$
with
$[T_\alpha ]$
with
![]() $[T]$
satisfying the following for all
$[T]$
satisfying the following for all
![]() $f \in [T]$
and ordinals
$f \in [T]$
and ordinals
![]() $\beta < \alpha $
:
$\beta < \alpha $
:
-
•
 ${{f}^{({\beta })}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\beta )}$
and, indeed,
${{f}^{({\beta })}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\beta )}$
and, indeed,
 ${{f}^{(\alpha )}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\alpha )}$
.
${{f}^{(\alpha )}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\alpha )}$
. -
•
 $f \nleq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
.
$f \nleq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
. -
• If
 $Y \leq _{\mathbf {T}} {{f}^{({\beta })}}$
then either
$Y \leq _{\mathbf {T}} {{f}^{({\beta })}}$
then either
 $Y \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
or
$Y \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
or
 $f \leq _{\mathbf {T}} Y \oplus {\mathbf {0}}^{(\beta +2)}$
.
$f \leq _{\mathbf {T}} Y \oplus {\mathbf {0}}^{(\beta +2)}$
.
Moreover, this holds with all possibility uniformity.
Note that the final point above immediately entails that if there is some
![]() $\beta < \alpha $
such that
$\beta < \alpha $
such that
![]() $Y \leq _{\mathbf {T}} {{f}^{({\beta })}}$
then there is some
$Y \leq _{\mathbf {T}} {{f}^{({\beta })}}$
then there is some
![]() $\gamma < \alpha $
such that either
$\gamma < \alpha $
such that either
![]() $Y \leq _{\mathbf {T}} {\mathbf {0}}^{(\gamma )}$
or
$Y \leq _{\mathbf {T}} {\mathbf {0}}^{(\gamma )}$
or
![]() $f \leq _{\mathbf {T}} {{Y}^{(\gamma )}}$
. We now catalogue a number of interesting corollaries, such as the existence of a
$f \leq _{\mathbf {T}} {{Y}^{(\gamma )}}$
. We now catalogue a number of interesting corollaries, such as the existence of a
![]() $\prod ^0_{2}$
singleton of minimal arithmetic degree.
$\prod ^0_{2}$
singleton of minimal arithmetic degree.
Corollary 4.3. There is a
![]() $\prod ^0_{2}$
singleton of minimal arithmetic degree.
$\prod ^0_{2}$
singleton of minimal arithmetic degree.
Proof Taking
![]() $T_\omega = {\left \{{\langle {0^n}\rangle }\mid {n \in \omega }\right \}}$
immediately produces a
$T_\omega = {\left \{{\langle {0^n}\rangle }\mid {n \in \omega }\right \}}$
immediately produces a
![]() $\prod ^0_{1}$
function singleton of minimal arithmetic degree and applying Lemma 2.1 transforms this into a
$\prod ^0_{1}$
function singleton of minimal arithmetic degree and applying Lemma 2.1 transforms this into a
![]() $\prod ^0_{2}$
singleton of minimal arithmetic degree.
$\prod ^0_{2}$
singleton of minimal arithmetic degree.
Our work from the previous section isn’t wasted as it allows us to prove the following interesting corollary.
Corollary 4.4. There is an arithmetically escaping function
![]() $f \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
such that every
$f \leq _{\mathbf {T}} {\mathbf {0}}^{(\omega )}$
such that every
![]() $X \leq _{\mathbf {a}} f$
is an arithmetic singleton.
$X \leq _{\mathbf {a}} f$
is an arithmetic singleton.
Proof By Corollary 4.3 and Lemma 2.1 let f be a
![]() $\prod ^0_{1}$
singleton of minimal arithmetic degree. By Lemma 2.2 f must be arithmetically escaping and by Proposition 3.10 every
$\prod ^0_{1}$
singleton of minimal arithmetic degree. By Lemma 2.2 f must be arithmetically escaping and by Proposition 3.10 every
![]() $Y \leq _{\mathbf {a}} f$
is an arithmetic singleton.
$Y \leq _{\mathbf {a}} f$
is an arithmetic singleton.
We can also derive some interesting consequences about perfect sets of minimal arithmetic degree.
Corollary 4.5. There is a perfect
![]() $\prod ^0_{2}$
class
$\prod ^0_{2}$
class
![]() $\mathscr {C}$
all of whose members are of minimal arithmetic degree and which contains elements of arbitrarily large non-domination strength.
$\mathscr {C}$
all of whose members are of minimal arithmetic degree and which contains elements of arbitrarily large non-domination strength.
By containing elements of arbitrarily large non-domination strength, we mean that for any countable
![]() $C \subset \omega ^{\omega }$
there is an
$C \subset \omega ^{\omega }$
there is an
![]() $X \in \mathscr {C}$
and
$X \in \mathscr {C}$
and
![]() $f \in \omega ^{\omega }$
such that
$f \in \omega ^{\omega }$
such that
![]() $X \equiv _{\mathbf {T}} f$
and f isn’t dominated by any
$X \equiv _{\mathbf {T}} f$
and f isn’t dominated by any
![]() $g \in C$
.
$g \in C$
.
Proof Take
![]() $T_\omega = \omega ^{<\omega }$
. Since
$T_\omega = \omega ^{<\omega }$
. Since
![]() $\Gamma $
is an f-tree and a homeomorphism at each
$\Gamma $
is an f-tree and a homeomorphism at each
![]() $\sigma \in T_\omega $
we can pick i large which ensures that
$\sigma \in T_\omega $
we can pick i large which ensures that
![]() $\Gamma (\sigma \widehat {\phantom {x}}\langle i\rangle )$
is large at
$\Gamma (\sigma \widehat {\phantom {x}}\langle i\rangle )$
is large at
![]() $n = \left \lvert \Gamma ^{\omega }_0(\sigma )\right \rvert $
. Thus, we can apply the same approach as in Corollary 3.3 to show that there is an element of
$n = \left \lvert \Gamma ^{\omega }_0(\sigma )\right \rvert $
. Thus, we can apply the same approach as in Corollary 3.3 to show that there is an element of
![]() $[T]$
that avoids domination by any element in C. By applying Lemma 2.1 we get a
$[T]$
that avoids domination by any element in C. By applying Lemma 2.1 we get a
![]() $\prod ^0_{2}$
class whose members are Turing equivalent to the elements in
$\prod ^0_{2}$
class whose members are Turing equivalent to the elements in
![]() $[T]$
.
$[T]$
.
Before we move on to providing proofs of Theorem 4.2 and Proposition 4.1, we end this section by asking a few questions. While the existence of a
![]() $\prod ^0_{2}$
singleton of minimal arithmetic degree is suggestive, it isn’t quite enough to demonstrate that the project of using the properties of fast growing functions to show
$\prod ^0_{2}$
singleton of minimal arithmetic degree is suggestive, it isn’t quite enough to demonstrate that the project of using the properties of fast growing functions to show
![]() $\omega \text {-REA}$
sets can’t be of minimal degree fails. This gives rise to the following question.
$\omega \text {-REA}$
sets can’t be of minimal degree fails. This gives rise to the following question.
Question 4.6. If f is arithmetically escaping, must there be some
![]() $X \leq _{\mathbf {a}} f$
where X isn’t of
$X \leq _{\mathbf {a}} f$
where X isn’t of
![]() $\omega \text {-REA}$
arithmetic degree.
$\omega \text {-REA}$
arithmetic degree.
At first glance, one might think that this question stands or falls with the existence of an
![]() $\omega \text {-REA}$
set of minimal arithmetic degree. After all, the question must have a negative answer if there is such an
$\omega \text {-REA}$
set of minimal arithmetic degree. After all, the question must have a negative answer if there is such an
![]() $ \omega \text {-REA}$
set and if the question has a positive answer then no such set can exist. However, there is still the possibility that the question has a negative answer and no
$ \omega \text {-REA}$
set and if the question has a positive answer then no such set can exist. However, there is still the possibility that the question has a negative answer and no
![]() $\omega \text {-REA}$
set is of minimal arithmetic degree. This would require that there is some non-arithmetic
$\omega \text {-REA}$
set is of minimal arithmetic degree. This would require that there is some non-arithmetic
![]() $\omega \text {-REA}$
set A such that every
$\omega \text {-REA}$
set A such that every
![]() $B \leq _{\mathbf {a}} A$
is arithmetically equivalent to an
$B \leq _{\mathbf {a}} A$
is arithmetically equivalent to an
![]() $\omega \text {-REA}$
set, but that doesn’t seem beyond the realm of possibility.
$\omega \text {-REA}$
set, but that doesn’t seem beyond the realm of possibility.
Next, inspired by the methods in [Reference Harrington5], we ask if this approach offers any utility if extended up through all ordinals below
![]() $\omega ^{\mathrm {CK}}_1$
.
$\omega ^{\mathrm {CK}}_1$
.
Question 4.7. Do results that create a unique path through
![]() $\mathcal {O}$
via ‘non-standard’ notations offer a means to extend Theorem 4.2 to prove interesting results about hyperdegrees?
$\mathcal {O}$
via ‘non-standard’ notations offer a means to extend Theorem 4.2 to prove interesting results about hyperdegrees?
Such a generalization isn’t as simple as merely applying the construction used in Theorem 4.2 to some non-standard notation. That can’t work as we could then build a
![]() $\prod ^0_{1}$
function singleton that isn’t of hyperarithmetic degree which contradicts the fact that if f is the unique path through a computable tree
$\prod ^0_{1}$
function singleton that isn’t of hyperarithmetic degree which contradicts the fact that if f is the unique path through a computable tree
![]() $[T]$
then
$[T]$
then
![]() $f \in \mathrm {HYP}$
. However, the methods in [Reference Harrington5] might allow the definition of a perfect
$f \in \mathrm {HYP}$
. However, the methods in [Reference Harrington5] might allow the definition of a perfect
![]() $\prod ^0_{1}$
class of elements all of which satisfy the conclusion of Theorem 4.2 with respect to all
$\prod ^0_{1}$
class of elements all of which satisfy the conclusion of Theorem 4.2 with respect to all
![]() $\alpha $
in some linearly ordered path through
$\alpha $
in some linearly ordered path through
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
Question 4.8. Is there a perfect
![]() $\prod ^0_{1}$
function class all of whose elements are both arithmetically minimal and arithmetically escaping?
$\prod ^0_{1}$
function class all of whose elements are both arithmetically minimal and arithmetically escaping?
The difficulty here is that modifying
![]() $T_\omega $
also results in modification to T.
$T_\omega $
also results in modification to T.
Question 4.9. What kind of ability do we have to control the join of pairs of minimal degrees? Are there
![]() $\prod ^0_{2}$
singletons
$\prod ^0_{2}$
singletons
![]() $A, B$
of minimal arithmetic degree such that
$A, B$
of minimal arithmetic degree such that
![]() $A \oplus B \equiv _{\mathbf {a}} {\mathbf {0}}^{(\omega )}$
(or even
$A \oplus B \equiv _{\mathbf {a}} {\mathbf {0}}^{(\omega )}$
(or even
![]() $\equiv _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
for arbitrary
$\equiv _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
for arbitrary
![]() $\beta \in \mathcal {O}$
). Could we combine this with the idea in Question 4.7 to create a perfect
$\beta \in \mathcal {O}$
). Could we combine this with the idea in Question 4.7 to create a perfect
![]() $\prod ^0_{2}$
class whose elements join to compute
$\prod ^0_{2}$
class whose elements join to compute
![]() $\mathcal {O}$
?
$\mathcal {O}$
?
5 Towers of trees
Before we get into the weeds of proving Proposition 4.1 we first show that it suffices to establish the main theorem. As not all readers may wish to delve into the details involved in manipulating ordinal notations we segregate the results needed to prove the claim for
![]() $\alpha $
above
$\alpha $
above
![]() $\omega $
into an appendix. If you are only interested in the case
$\omega $
into an appendix. If you are only interested in the case
![]() $\alpha = \omega $
you may simply take
$\alpha = \omega $
you may simply take
![]() ${\beta }^{\Diamond } = \omega $
and
${\beta }^{\Diamond } = \omega $
and
![]() $l^{\Diamond }(n) = n$
for all
$l^{\Diamond }(n) = n$
for all
![]() $n \in \omega $
and
$n \in \omega $
and
![]() ${\left \{\omega \right \}}^{\mathcal {O}}(n) = 2n$
and replace the following definition of an even notation with that of an even number.
${\left \{\omega \right \}}^{\mathcal {O}}(n) = 2n$
and replace the following definition of an even notation with that of an even number.
Definition 5.1. The ordinal notation
![]() $\beta $
is an even notation if
$\beta $
is an even notation if
![]() $\beta = \lambda + 2k$
where
$\beta = \lambda + 2k$
where
![]() $\lambda $
is either
$\lambda $
is either
![]() $0$
or a limit notation and
$0$
or a limit notation and
![]() $k \in \omega $
.
$k \in \omega $
.
We break our proof of Theorem 4.2 into a construction of a uniform sequence of trees
![]() $T_\beta $
and a verification that this uniform sequence of trees has the desired properties.
$T_\beta $
and a verification that this uniform sequence of trees has the desired properties.
Proposition 5.2. Given a limit notation
![]() $\alpha $
and a tree
$\alpha $
and a tree
![]() $T_{\alpha }$
computable in
$T_{\alpha }$
computable in
![]() ${\mathbf {0}}^{(\alpha )}$
the following hold:
${\mathbf {0}}^{(\alpha )}$
the following hold:
-
1. For each even notation
 $\beta <_{\mathcal {O}} \alpha $
there is a tree
$\beta <_{\mathcal {O}} \alpha $
there is a tree
 $T_\beta $
uniformly computable in
$T_\beta $
uniformly computable in
 ${\mathbf {0}}^{(\beta )}$
.
${\mathbf {0}}^{(\beta )}$
. -
2. For all
 $\gamma <_{\mathcal {O}} \beta \leq _{\mathcal {O}} \alpha $
, there is a uniformly given f-tree
$\gamma <_{\mathcal {O}} \beta \leq _{\mathcal {O}} \alpha $
, there is a uniformly given f-tree
 $\Gamma ^{\beta }_\gamma \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
that’s a homeomorphism of
$\Gamma ^{\beta }_\gamma \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
that’s a homeomorphism of
 $[T_\beta ]$
with
$[T_\beta ]$
with
 $[T_\gamma ]$
.
$[T_\gamma ]$
. -
3. For each even notation
 $\beta <_{\mathcal {O}} \alpha $
there is some
$\beta <_{\mathcal {O}} \alpha $
there is some
 $l^{\Diamond }(\beta ) \in \omega $
such that if
$l^{\Diamond }(\beta ) \in \omega $
such that if
 $\sigma \in T_\beta , \lvert \sigma \rvert = l^{\Diamond }(\beta )$
then applying Proposition 4.1 with
$\sigma \in T_\beta , \lvert \sigma \rvert = l^{\Diamond }(\beta )$
then applying Proposition 4.1 with  and
and
 $X = {\mathbf {0}}^{(\beta )}$
produces
$X = {\mathbf {0}}^{(\beta )}$
produces  and
and
 $\hat {T}$
where
$\hat {T}$
where
 $\sigma \widehat {\phantom {x}} \hat {T}(\tau ) = \Gamma ^{\beta +2}_{\beta }(\sigma \widehat {\phantom {x}}\tau )$
for all
$\sigma \widehat {\phantom {x}} \hat {T}(\tau ) = \Gamma ^{\beta +2}_{\beta }(\sigma \widehat {\phantom {x}}\tau )$
for all
 $\tau $
.
$\tau $
.
For 2 we understand the uniformity claim to mean that
![]() $\Gamma ^{\beta }_\gamma (\tau )$
is given by
$\Gamma ^{\beta }_\gamma (\tau )$
is given by
![]() $\Gamma (\beta , \gamma , {\mathbf {0}}^{(\beta )}, \tau )$
for a single computable functional
$\Gamma (\beta , \gamma , {\mathbf {0}}^{(\beta )}, \tau )$
for a single computable functional
![]() $\Gamma $
. Similarly, for 1 we understand the uniformity claim to mean that there is a single computable functional such that
$\Gamma $
. Similarly, for 1 we understand the uniformity claim to mean that there is a single computable functional such that
![]() $\Upsilon (\beta , {\mathbf {0}}^{(\beta )}, \cdot )$
gives the characteristic function for
$\Upsilon (\beta , {\mathbf {0}}^{(\beta )}, \cdot )$
gives the characteristic function for
![]() $T_\beta $
for all even notations
$T_\beta $
for all even notations
![]() $\beta \leq _{\mathcal {O}} \alpha $
, Moreover, that indexes for both functionals are given by a computable function of
$\beta \leq _{\mathcal {O}} \alpha $
, Moreover, that indexes for both functionals are given by a computable function of
![]() $\alpha $
and an index for
$\alpha $
and an index for
![]() $T_\alpha $
.
$T_\alpha $
.
5.1 Verifying the main theorem
We now prove a utility lemma which will let us show that Theorem 4.2 follows from the claim above.
Lemma 5.3. Given
![]() $\alpha , T_\beta , \Gamma $
as in Proposition 5.2 and
$\alpha , T_\beta , \Gamma $
as in Proposition 5.2 and
![]() $f \in [T_0]$
for all even notations
$f \in [T_0]$
for all even notations
![]() $\beta \leq _{\mathcal {O}} \alpha $
:
$\beta \leq _{\mathcal {O}} \alpha $
:
-
1. There is a unique
 $g_\beta \in [T_\beta ]$
such that
$g_\beta \in [T_\beta ]$
such that
 $\Gamma ^{\beta }_{0}(g_\beta ) = f$
.
$\Gamma ^{\beta }_{0}(g_\beta ) = f$
. -
2.
 $g_\beta $
is uniformly computable from
$g_\beta $
is uniformly computable from
 $f \oplus {\mathbf {0}}^{(\beta )}$
.
$f \oplus {\mathbf {0}}^{(\beta )}$
. -
3.
 ${{f}^{({\beta })}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\beta )} \equiv _{\mathbf {T}} g_\beta \oplus {\mathbf {0}}^{(\beta )}$
. Moreover, this equivalence holds uniformly in
${{f}^{({\beta })}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\beta )} \equiv _{\mathbf {T}} g_\beta \oplus {\mathbf {0}}^{(\beta )}$
. Moreover, this equivalence holds uniformly in
 $\beta $
.
$\beta $
. -
4.
 $\beta <_{\mathcal {O}} \alpha $
implies
$\beta <_{\mathcal {O}} \alpha $
implies
 $g_\beta \nleq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
.
$g_\beta \nleq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
. -
5. If
 $\beta <_{\mathcal {O}} \alpha $
and
$\beta <_{\mathcal {O}} \alpha $
and
 $Y \leq _{\mathbf {T}} g_\beta \oplus {\mathbf {0}}^{(\beta )}$
then either
$Y \leq _{\mathbf {T}} g_\beta \oplus {\mathbf {0}}^{(\beta )}$
then either
 $Y \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
or
$Y \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
or
 $g_\beta \leq _{\mathbf {T}} Y \oplus {\mathbf {0}}^{(\beta +2)}$
.
$g_\beta \leq _{\mathbf {T}} Y \oplus {\mathbf {0}}^{(\beta +2)}$
.
Proof By point 2 of Proposition 5.2 there is a unique
![]() $g_{\beta }$
whose image under
$g_{\beta }$
whose image under
![]() $\Gamma ^{\beta }_0$
is f. We can compute
$\Gamma ^{\beta }_0$
is f. We can compute
![]() $g_\beta $
in
$g_\beta $
in
![]() ${\mathbf {0}}^{(\beta )} \oplus f$
as
${\mathbf {0}}^{(\beta )} \oplus f$
as
![]() $ \Gamma ^{\beta }_0 \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
and as it’s an f-tree it sends incompatible elements in the domain to incompatible elements in the range. This verifies points 1 and 2.
$ \Gamma ^{\beta }_0 \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
and as it’s an f-tree it sends incompatible elements in the domain to incompatible elements in the range. This verifies points 1 and 2.
For point 4 let
![]() $\sigma = g_\beta {{\restriction _{{l^{\Diamond }(\beta )}}}}$
and note that by 3 of Proposition 5.2 for
$\sigma = g_\beta {{\restriction _{{l^{\Diamond }(\beta )}}}}$
and note that by 3 of Proposition 5.2 for
![]() $\beta <_{\mathcal {O}} \alpha $
the tree
$\beta <_{\mathcal {O}} \alpha $
the tree ![]() is the result of Proposition 4.1 applied to
is the result of Proposition 4.1 applied to ![]() and by 3 of Proposition 4.1 we know that
and by 3 of Proposition 4.1 we know that
![]() $ g_{\beta } \nleq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
. By part 5 of Proposition 4.1 we have that 5 holds. This leaves us only 3 to verify.
$ g_{\beta } \nleq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
. By part 5 of Proposition 4.1 we have that 5 holds. This leaves us only 3 to verify.
Suppose that 3 holds for all notations
![]() $\gamma <_{\mathcal {O}} \beta $
(where we regard the claim as trivially true for odd notations). We prove the claim holds for
$\gamma <_{\mathcal {O}} \beta $
(where we regard the claim as trivially true for odd notations). We prove the claim holds for
![]() $\beta $
. First, suppose that
$\beta $
. First, suppose that
![]() $\beta = \gamma + 2$
.
$\beta = \gamma + 2$
.
Now let
![]() $\sigma = g_\gamma {{\restriction _{l^{\Diamond }(\gamma )}}}$
. By 3 of Proposition 5.2 the tree
$\sigma = g_\gamma {{\restriction _{l^{\Diamond }(\gamma )}}}$
. By 3 of Proposition 5.2 the tree ![]() is the result of Proposition 4.1 applied to
is the result of Proposition 4.1 applied to ![]() . Thus, by point 4 of Proposition 4.1 we have
. Thus, by point 4 of Proposition 4.1 we have
![]() ${\left (g_\gamma \oplus {\mathbf {0}}^{(\gamma )}\right )}^{\prime \prime } \equiv _{\mathbf {T}} g_\gamma \oplus {\mathbf {0}}^{(\gamma +2)} \equiv _{\mathbf {T}} g_{\gamma +2} \oplus {\mathbf {0}}^{(\gamma +2)}$
. The inductive assumption transforms this equivalence into the one asserted in 3.
${\left (g_\gamma \oplus {\mathbf {0}}^{(\gamma )}\right )}^{\prime \prime } \equiv _{\mathbf {T}} g_\gamma \oplus {\mathbf {0}}^{(\gamma +2)} \equiv _{\mathbf {T}} g_{\gamma +2} \oplus {\mathbf {0}}^{(\gamma +2)}$
. The inductive assumption transforms this equivalence into the one asserted in 3.
Now, suppose that
![]() $\beta $
is a limit notation. Note that as Proposition 5.2 guarantees that
$\beta $
is a limit notation. Note that as Proposition 5.2 guarantees that
![]() $T_\gamma $
is uniformly computable from
$T_\gamma $
is uniformly computable from
![]() ${\mathbf {0}}^{(\gamma )}$
(for
${\mathbf {0}}^{(\gamma )}$
(for
![]() $\gamma $
an even notation) and Proposition 4.1 holds uniformly therefore claim 3 holds uniformly below
$\gamma $
an even notation) and Proposition 4.1 holds uniformly therefore claim 3 holds uniformly below
![]() $\beta $
. But
$\beta $
. But
![]() ${\mathbf {0}}^{(\beta )}$
can uniformly compute
${\mathbf {0}}^{(\beta )}$
can uniformly compute
![]() ${\mathbf {0}}^{(\gamma )}$
and thus
${\mathbf {0}}^{(\gamma )}$
and thus
![]() $f \oplus {\mathbf {0}}^{(\beta )}$
can compute
$f \oplus {\mathbf {0}}^{(\beta )}$
can compute
![]() ${{f}^{(\gamma )}}$
for notations
${{f}^{(\gamma )}}$
for notations
![]() $\gamma <_{\mathcal {O}} \beta $
. Hence
$\gamma <_{\mathcal {O}} \beta $
. Hence
![]() $f \oplus {\mathbf {0}}^{(\beta )}$
can compute
$f \oplus {\mathbf {0}}^{(\beta )}$
can compute
![]() ${{f}^{({\beta })}}$
which is automatically an equivalence. Using
${{f}^{({\beta })}}$
which is automatically an equivalence. Using
![]() $\Gamma ^{\beta }_0 \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
to translate between
$\Gamma ^{\beta }_0 \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
to translate between
![]() $g_\beta $
and f we see
$g_\beta $
and f we see
![]() $f \oplus {\mathbf {0}}^{(\beta )} \equiv _{\mathbf {T}} g \oplus {\mathbf {0}}^{(\beta )}$
completing the verification.
$f \oplus {\mathbf {0}}^{(\beta )} \equiv _{\mathbf {T}} g \oplus {\mathbf {0}}^{(\beta )}$
completing the verification.
We can now show that Theorem 4.2 follows from Proposition 5.2.
Proof Take
![]() $\alpha '$
to be a notation for the desired ordinal in Theorem 4.2 and apply Proposition 5.2 to get the notation
$\alpha '$
to be a notation for the desired ordinal in Theorem 4.2 and apply Proposition 5.2 to get the notation
![]() $\alpha $
, the sequence
$\alpha $
, the sequence
![]() $T_\beta $
and
$T_\beta $
and
![]() $\Gamma $
. We now apply Lemma 5.3. The equivalence
$\Gamma $
. We now apply Lemma 5.3. The equivalence
![]() ${{f}^{({\beta })}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\beta )} \equiv _{\mathbf {T}} g_\beta \oplus {\mathbf {0}}^{(\beta )}$
from part 3 of Lemma 5.3 gives the first claim in Theorem 4.2 on its own. Applying it to part 5 of Lemma 5.3 is enough to give the final claim in Theorem 4.2. Finally, if
${{f}^{({\beta })}} \equiv _{\mathbf {T}} f \oplus {\mathbf {0}}^{(\beta )} \equiv _{\mathbf {T}} g_\beta \oplus {\mathbf {0}}^{(\beta )}$
from part 3 of Lemma 5.3 gives the first claim in Theorem 4.2 on its own. Applying it to part 5 of Lemma 5.3 is enough to give the final claim in Theorem 4.2. Finally, if
![]() $f \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
then that equivalence implies that
$f \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
then that equivalence implies that
![]() $g_\beta \oplus {\mathbf {0}}^{(\beta )} \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
contradicting part 4 of Lemma 5.3.
$g_\beta \oplus {\mathbf {0}}^{(\beta )} \leq _{\mathbf {T}} {\mathbf {0}}^{(\beta )}$
contradicting part 4 of Lemma 5.3.
5.2 Constructing the tower
We now prove Proposition 5.2 follows from Proposition 4.1. To deal with notations for ordinals above
![]() $\omega $
we use some results proved in Appendices A and B. We start by defining
$\omega $
we use some results proved in Appendices A and B. We start by defining
![]() $ l^{\Diamond }(\beta ), {\beta }^{\Diamond }$
via Definition B.3. As mentioned above, readers only interested in the case
$ l^{\Diamond }(\beta ), {\beta }^{\Diamond }$
via Definition B.3. As mentioned above, readers only interested in the case
![]() $\alpha = \omega $
can skip the material on ordinal notations in Appendices A and B. They will, however, still need to know that we can replace
$\alpha = \omega $
can skip the material on ordinal notations in Appendices A and B. They will, however, still need to know that we can replace
![]() $T_\omega $
with a tree
$T_\omega $
with a tree
![]() $T^{\prime }_\omega $
with
$T^{\prime }_\omega $
with
![]() $[T^{\prime }_\omega ] = [T_\omega ]$
in which the membership of
$[T^{\prime }_\omega ] = [T_\omega ]$
in which the membership of
![]() $\sigma \in T^{\prime }_\omega $
for
$\sigma \in T^{\prime }_\omega $
for
![]() $\lvert \sigma \rvert = 2n$
can be computed uniformly in
$\lvert \sigma \rvert = 2n$
can be computed uniformly in
![]() ${\mathbf {0}}^{(2n)}$
(a special case of the general result proved in Lemma B.6).
${\mathbf {0}}^{(2n)}$
(a special case of the general result proved in Lemma B.6).
We construct a computable functional
![]() $\Upsilon $
such that for all even notations
$\Upsilon $
such that for all even notations
![]() $\beta $
with
$\beta $
with
![]() $\beta \leq _{\mathcal {O}} \alpha $
,
$\beta \leq _{\mathcal {O}} \alpha $
,
![]() $\Upsilon (\beta , {\mathbf {0}}^{(\beta )}, \cdot )$
gives the characteristic function for
$\Upsilon (\beta , {\mathbf {0}}^{(\beta )}, \cdot )$
gives the characteristic function for
![]() $T_\beta $
. Regarding functionals as r.e-sets of axioms we can define a functional
$T_\beta $
. Regarding functionals as r.e-sets of axioms we can define a functional
![]() $\Upsilon $
assuming that we already have access to some partial functional
$\Upsilon $
assuming that we already have access to some partial functional
![]() $\hat {\Upsilon }$
and then use the recursion theorem to yield a single functional satisfying
$\hat {\Upsilon }$
and then use the recursion theorem to yield a single functional satisfying
![]() $\Upsilon = \tilde {\Upsilon }$
. Formally speaking,
$\Upsilon = \tilde {\Upsilon }$
. Formally speaking,
![]() $\Upsilon $
and
$\Upsilon $
and
![]() $\tilde {\Upsilon }$
are defined to be sets of axioms; however, we will only specify those sets implicitly by instead defining the trees
$\tilde {\Upsilon }$
are defined to be sets of axioms; however, we will only specify those sets implicitly by instead defining the trees
![]() $T_\beta $
in terms of the trees
$T_\beta $
in terms of the trees
![]() $\tilde {T}_\beta $
where we understand that
$\tilde {T}_\beta $
where we understand that
![]() $\tilde {T}_\beta $
represents the set defined by
$\tilde {T}_\beta $
represents the set defined by
![]() $\tilde {\Upsilon }(\beta , X, \cdot )$
on the guess that
$\tilde {\Upsilon }(\beta , X, \cdot )$
on the guess that
![]() $X = {\mathbf {0}}^{(\beta )}$
.
$X = {\mathbf {0}}^{(\beta )}$
.
Specifically, we define
![]() $T_\alpha $
to be
$T_\alpha $
to be
![]() $T_\alpha $
. That is, regardless of the behaviour of
$T_\alpha $
. That is, regardless of the behaviour of
![]() $\tilde {\Upsilon }$
,
$\tilde {\Upsilon }$
,
![]() $\Upsilon (\alpha , X, \cdot )$
gives the computation that yields the characteristic function for
$\Upsilon (\alpha , X, \cdot )$
gives the computation that yields the characteristic function for
![]() $ T_\alpha $
when
$ T_\alpha $
when
![]() $X = {\mathbf {0}}^{(\alpha )}$
. Given
$X = {\mathbf {0}}^{(\alpha )}$
. Given
![]() $\beta $
an even notation with
$\beta $
an even notation with
![]() $\beta <_{\mathcal {O}} \alpha $
we define the tree
$\beta <_{\mathcal {O}} \alpha $
we define the tree
![]() $T_\beta $
as follows (once
$T_\beta $
as follows (once
![]() $\Upsilon $
has verified the
$\Upsilon $
has verified the
![]() $\Sigma ^1_1$
fact that
$\Sigma ^1_1$
fact that
![]() $\beta <_{\mathcal {O}} \alpha $
is an even notation).
$\beta <_{\mathcal {O}} \alpha $
is an even notation).
Let
![]() $\lambda = {\beta }^{\Diamond }$
. If
$\lambda = {\beta }^{\Diamond }$
. If
![]() $\lvert \sigma \rvert \leq l^{\Diamond }(\beta )$
then
$\lvert \sigma \rvert \leq l^{\Diamond }(\beta )$
then
![]() $\sigma \in T_\beta $
iff
$\sigma \in T_\beta $
iff
![]() $\sigma \in \tilde {T}^{\prime }_\lambda $
where if
$\sigma \in \tilde {T}^{\prime }_\lambda $
where if
![]() $\lambda $
is a limit notation,
$\lambda $
is a limit notation,
![]() $\tilde {T}^{\prime }_\lambda $
is the result of applying Lemma B.6 to
$\tilde {T}^{\prime }_\lambda $
is the result of applying Lemma B.6 to
![]() $\tilde {T}_\lambda $
so that
$\tilde {T}_\lambda $
so that
![]() $\tilde {T}^{\prime }_\lambda {{\restriction _{l^{\Diamond }(\beta )}}}$
has membership uniformly computable in
$\tilde {T}^{\prime }_\lambda {{\restriction _{l^{\Diamond }(\beta )}}}$
has membership uniformly computable in
![]() ${\mathbf {0}}^{(\beta )}$
and
${\mathbf {0}}^{(\beta )}$
and
![]() $[\tilde {T}^{\prime }_\lambda ]$
=
$[\tilde {T}^{\prime }_\lambda ]$
=
![]() $ [\tilde {T}_\lambda ]$
. If
$ [\tilde {T}_\lambda ]$
. If
![]() $\lambda $
is a successor notation then
$\lambda $
is a successor notation then
![]() $\tilde {T}^{\prime }_\lambda = \tilde {T}_\lambda $
.
$\tilde {T}^{\prime }_\lambda = \tilde {T}_\lambda $
.
For
![]() $\sigma '$
with
$\sigma '$
with
![]() $\left \lvert \sigma '\right \rvert> l^{\Diamond }(\beta )$
let
$\left \lvert \sigma '\right \rvert> l^{\Diamond }(\beta )$
let
![]() $\sigma ' = \sigma \widehat {\phantom {x}} \tau $
where
$\sigma ' = \sigma \widehat {\phantom {x}} \tau $
where
![]() $\lvert \sigma \rvert = l^{\Diamond }(\beta )$
. Set
$\lvert \sigma \rvert = l^{\Diamond }(\beta )$
. Set
![]() $\sigma ' \notin T_\beta $
if
$\sigma ' \notin T_\beta $
if
![]() $\sigma \notin \tilde {T}^{\prime }_\lambda $
. If
$\sigma \notin \tilde {T}^{\prime }_\lambda $
. If
![]() $\sigma \in \tilde {T}^{\prime }_\lambda $
then apply Proposition 4.1 to
$\sigma \in \tilde {T}^{\prime }_\lambda $
then apply Proposition 4.1 to ![]() to yield some
to yield some
![]() $T^{\sigma }_\beta $
and place
$T^{\sigma }_\beta $
and place
![]() $\sigma ' \in T_\beta $
just if
$\sigma ' \in T_\beta $
just if
![]() $\tau \in T^{\sigma }_\beta $
. Note that, we can enforce the fact that
$\tau \in T^{\sigma }_\beta $
. Note that, we can enforce the fact that
![]() $\tilde {T}^{\sigma }_{\beta +2}$
is always a tree by only allowing strings into this set when all their predecessors have been seen to be in the set.
$\tilde {T}^{\sigma }_{\beta +2}$
is always a tree by only allowing strings into this set when all their predecessors have been seen to be in the set.
We now define
![]() $\Upsilon $
to be the fixed point rendering
$\Upsilon $
to be the fixed point rendering
![]() $\tilde {\Upsilon } = \Upsilon $
. Thus, for an even notation
$\tilde {\Upsilon } = \Upsilon $
. Thus, for an even notation
![]() $\beta \leq _{\mathcal {O}} \alpha $
we define
$\beta \leq _{\mathcal {O}} \alpha $
we define
![]() $T_\beta = \Upsilon (\beta , {\mathbf {0}}^{(\beta )})$
. Note that, by part 3 of Proposition B.5 we can be sure that our fixed point will satisfy
$T_\beta = \Upsilon (\beta , {\mathbf {0}}^{(\beta )})$
. Note that, by part 3 of Proposition B.5 we can be sure that our fixed point will satisfy
![]() $T_\beta {{\restriction _{l^{\Diamond }(\beta )}}} \subset T_{\beta +2}{{\restriction _{{l^{\Diamond }(\beta )}}}}$
so that
$T_\beta {{\restriction _{l^{\Diamond }(\beta )}}} \subset T_{\beta +2}{{\restriction _{{l^{\Diamond }(\beta )}}}}$
so that
![]() $ \tilde {T}^{\sigma }_{\beta +2}$
will be defined for
$ \tilde {T}^{\sigma }_{\beta +2}$
will be defined for
![]() $\sigma \in T_{\beta }, \lvert \sigma \rvert = l^{\Diamond }(\beta )$
.
$\sigma \in T_{\beta }, \lvert \sigma \rvert = l^{\Diamond }(\beta )$
.
We define the functional
![]() $\Gamma $
in a similar fashion assuming we have some
$\Gamma $
in a similar fashion assuming we have some
![]() $\tilde {\Gamma }$
and applying the recursion theorem. Note that, the argument above produces two indexes i and
$\tilde {\Gamma }$
and applying the recursion theorem. Note that, the argument above produces two indexes i and
![]() $q(i)$
for the functional
$q(i)$
for the functional
![]() $\Upsilon $
where q is the computable functional implicitly defined by the construction above and i is the index given by the recursion theorem applied to q. While i and
$\Upsilon $
where q is the computable functional implicitly defined by the construction above and i is the index given by the recursion theorem applied to q. While i and
![]() $q(i)$
result in the same set of axioms, we can’t guarantee that the application of Proposition 4.1 produces the same
$q(i)$
result in the same set of axioms, we can’t guarantee that the application of Proposition 4.1 produces the same
![]() $T, \hat {T}$
for different indexes for the same tree S. To handle this issue, we use
$T, \hat {T}$
for different indexes for the same tree S. To handle this issue, we use
![]() $\tilde {T}_{\beta + 2}$
to indicate the definition in terms of i and apply Proposition 4.1 to
$\tilde {T}_{\beta + 2}$
to indicate the definition in terms of i and apply Proposition 4.1 to ![]() not
not ![]() to ensure we get the f-tree
to ensure we get the f-tree
![]() $\hat {T}$
associated with the construction of
$\hat {T}$
associated with the construction of ![]() .
.
With this in mind, we define
![]() $\Gamma ^{\beta +2}_\beta $
for
$\Gamma ^{\beta +2}_\beta $
for
![]() $\beta \leq _{\mathcal {O}} \alpha $
an even notation as follows. If
$\beta \leq _{\mathcal {O}} \alpha $
an even notation as follows. If
![]() ${\lvert \sigma \rvert \leq l^{\Diamond }(\beta )}$
then
${\lvert \sigma \rvert \leq l^{\Diamond }(\beta )}$
then
![]() $\Gamma ^{\beta +2}_\beta (\sigma ) = \sigma $
if
$\Gamma ^{\beta +2}_\beta (\sigma ) = \sigma $
if
![]() $\sigma \in \tilde {T}_{\beta + 2}$
and undefined otherwise. If
$\sigma \in \tilde {T}_{\beta + 2}$
and undefined otherwise. If
![]() $\left \lvert \sigma '\right \rvert> l^{\Diamond }(\beta )$
then let
$\left \lvert \sigma '\right \rvert> l^{\Diamond }(\beta )$
then let
![]() $\sigma = \sigma '{{\restriction _{{l^{\Diamond }(\beta )}}}}$
and if
$\sigma = \sigma '{{\restriction _{{l^{\Diamond }(\beta )}}}}$
and if
![]() $\sigma \notin \tilde {T}_{\beta + 2}$
then
$\sigma \notin \tilde {T}_{\beta + 2}$
then
![]() $\Gamma ^{\beta +2}_\beta (\sigma ')\uparrow $
. Otherwise, we define
$\Gamma ^{\beta +2}_\beta (\sigma ')\uparrow $
. Otherwise, we define
![]() $\Gamma ^{\beta +2}_\beta (\sigma ') = \sigma \widehat {\phantom {x}} \hat {T}(\tau )$
where,
$\Gamma ^{\beta +2}_\beta (\sigma ') = \sigma \widehat {\phantom {x}} \hat {T}(\tau )$
where,
![]() $\sigma ' = \sigma \widehat {\phantom {x}} \tau $
and
$\sigma ' = \sigma \widehat {\phantom {x}} \tau $
and
![]() $\hat {T}$
is the f-tree produced by Proposition 4.1 as applied to
$\hat {T}$
is the f-tree produced by Proposition 4.1 as applied to ![]() . For
. For
![]() $\beta ' <_{\mathcal {O}} \beta $
we define
$\beta ' <_{\mathcal {O}} \beta $
we define
![]() $ \Gamma ^{\beta +2}_{\beta '}$
to be
$ \Gamma ^{\beta +2}_{\beta '}$
to be
![]() $\Gamma ^{\beta +2}_{\beta } \circ \tilde {\Gamma }^{\beta }_{\beta '}$
.
$\Gamma ^{\beta +2}_{\beta } \circ \tilde {\Gamma }^{\beta }_{\beta '}$
.
Finally, for
![]() $\lambda $
a limit and
$\lambda $
a limit and
![]() $\beta <_{\mathcal {O}} \lambda \leq _{\mathcal {O}} \alpha $
,
$\beta <_{\mathcal {O}} \lambda \leq _{\mathcal {O}} \alpha $
,
![]() $\beta $
an even notation we define
$\beta $
an even notation we define
![]() $\Gamma ^{\lambda }_{\beta }(\sigma )$
as follows. Let
$\Gamma ^{\lambda }_{\beta }(\sigma )$
as follows. Let
![]() $\beta _n$
be the sequence of notations given by part 4 of Proposition B.5. Let m be the least with
$\beta _n$
be the sequence of notations given by part 4 of Proposition B.5. Let m be the least with
![]() $\lvert \sigma \rvert \leq m$
and
$\lvert \sigma \rvert \leq m$
and
![]() $\beta \leq _{\mathcal {O}} \beta _m$
and define
$\beta \leq _{\mathcal {O}} \beta _m$
and define
![]() $\Gamma ^{\lambda }_{\beta }(\sigma )$
to be equal to
$\Gamma ^{\lambda }_{\beta }(\sigma )$
to be equal to
![]() $ \tilde {\Gamma }^{\beta _m}_{\beta }(\sigma )$
. Finally, we define
$ \tilde {\Gamma }^{\beta _m}_{\beta }(\sigma )$
. Finally, we define
![]() $\Gamma $
via the recursion theorem so that
$\Gamma $
via the recursion theorem so that
![]() $\Gamma = \tilde {\Gamma }$
.
$\Gamma = \tilde {\Gamma }$
.
To verify this construction produces the desired result, we suppose that
![]() $\beta , \gamma $
is the lexicographically least pair of even notations
$\beta , \gamma $
is the lexicographically least pair of even notations
![]() $\gamma <_{\mathcal {O}} \beta \leq _{\mathcal {O}} \alpha $
such that
$\gamma <_{\mathcal {O}} \beta \leq _{\mathcal {O}} \alpha $
such that
![]() $\Gamma ^{\beta }_\gamma $
isn’t an f-tree that’s a homeomorphism of
$\Gamma ^{\beta }_\gamma $
isn’t an f-tree that’s a homeomorphism of
![]() $[T_\beta ]$
with
$[T_\beta ]$
with
![]() $[T_\gamma ]$
and then observe that if
$[T_\gamma ]$
and then observe that if
![]() $\beta = \beta ' + 2$
then since
$\beta = \beta ' + 2$
then since
![]() $\Gamma ^{\beta '+2}_{\beta '}$
is a homeomorphism we get a contradiction. Similarly, if
$\Gamma ^{\beta '+2}_{\beta '}$
is a homeomorphism we get a contradiction. Similarly, if
![]() $ \lambda = \beta $
is a limit then by Proposition B.5, 6 of Proposition 4.1, and the inductive assumption regarding
$ \lambda = \beta $
is a limit then by Proposition B.5, 6 of Proposition 4.1, and the inductive assumption regarding
![]() $\Gamma ^{\beta _n}_\beta $
we can derive that
$\Gamma ^{\beta _n}_\beta $
we can derive that
![]() $\Gamma ^{\lambda }_\beta $
is an f-tree that’s a homeomorphism of
$\Gamma ^{\lambda }_\beta $
is an f-tree that’s a homeomorphism of
![]() $[T_\lambda ]$
with its image contained in
$[T_\lambda ]$
with its image contained in
![]() $[T_\beta ]$
. Now suppose that some
$[T_\beta ]$
. Now suppose that some
![]() $f \in [T_\beta ]$
isn’t equal to
$f \in [T_\beta ]$
isn’t equal to
![]() $\Gamma ^{\lambda }_\beta (g)$
for any
$\Gamma ^{\lambda }_\beta (g)$
for any
![]() $g \in [T_\lambda ]$
. Then, for some n we have that
$g \in [T_\lambda ]$
. Then, for some n we have that
![]() $f \succ \Gamma ^{\beta _n}_\beta (\sigma )$
for no
$f \succ \Gamma ^{\beta _n}_\beta (\sigma )$
for no
![]() $\sigma \in T^{\prime }_\lambda $
with
$\sigma \in T^{\prime }_\lambda $
with
![]() $\lvert \sigma \rvert = l^{\Diamond }(\beta _n)$
and thus by the inductive assumption
$\lvert \sigma \rvert = l^{\Diamond }(\beta _n)$
and thus by the inductive assumption
![]() $f \notin [T_\beta ]$
. Thus, the claim holds for
$f \notin [T_\beta ]$
. Thus, the claim holds for
![]() $\Gamma ^{\lambda }_\beta $
as well. This suffices to prove Proposition 5.2.
$\Gamma ^{\lambda }_\beta $
as well. This suffices to prove Proposition 5.2.
6 Minimality and double jump inversion
In this section, we finally present the proof of Proposition 4.1. However, before we do this we answer an obvious question raised by our construction. Why do we use double jump inversion and not single jump inversion as Harrington did in [Reference Harrington5]? The answer is that it’s not possible. We can’t satisfy the minimality style requirements while also using
![]() $\omega $
-branching to encode the copy of
$\omega $
-branching to encode the copy of
![]() $ T_{\beta + 1}$
. Specifically, we now show that no
$ T_{\beta + 1}$
. Specifically, we now show that no
![]() ${\mathbf {0}}'$
${\mathbf {0}}'$
![]() $\omega $
-branching tree T lets us achieve the kind of minimality required by part 5 of Proposition 4.1.
$\omega $
-branching tree T lets us achieve the kind of minimality required by part 5 of Proposition 4.1.
Proposition 6.1. Given a perfect weakly
![]() $\omega $
-branching pruned f-tree
$\omega $
-branching pruned f-tree
![]() $T \leq _{\mathbf {T}} {\mathbf {0}}'$
one can uniformly construct a computable functional
$T \leq _{\mathbf {T}} {\mathbf {0}}'$
one can uniformly construct a computable functional
![]() $\Phi $
such that e-splitting pairs in T occur above every node in T and for every
$\Phi $
such that e-splitting pairs in T occur above every node in T and for every
![]() $\tau \in \mathrm {rng} T$
there are paths
$\tau \in \mathrm {rng} T$
there are paths
![]() $f \neq g$
extending
$f \neq g$
extending
![]() $\tau $
through T with
$\tau $
through T with
![]() $\Phi _{e}\left (f\right ) = \Phi _{e}\left (g\right )$
.
$\Phi _{e}\left (f\right ) = \Phi _{e}\left (g\right )$
.
Indeed, the result is actually slightly stronger in that we show that even if T is unpruned we can start building such
![]() $f, g$
above every node in T and always extend to preserve agreement under
$f, g$
above every node in T and always extend to preserve agreement under
![]() $\Phi _{e}$
until we hit a terminal node. Even without this improvement, this rules out the possibility of building
$\Phi _{e}$
until we hit a terminal node. Even without this improvement, this rules out the possibility of building
![]() $\hat {T}$
to be computable in
$\hat {T}$
to be computable in
![]() ${X}^{\prime }$
. While we aren’t guaranteed that
${X}^{\prime }$
. While we aren’t guaranteed that
![]() $\hat {T}$
itself is pruned it will be pruned whenever S is pruned. Thus, the above result rules out the possibility of performing the construction using only single jump inversion. Since the proof of this proposition takes some work and would interrupt the flow of the paper we relegate it to Appendix A.
$\hat {T}$
itself is pruned it will be pruned whenever S is pruned. Thus, the above result rules out the possibility of performing the construction using only single jump inversion. Since the proof of this proposition takes some work and would interrupt the flow of the paper we relegate it to Appendix A.
6.1 Machinery
The construction will build T via a stagewise approximation
![]() $T_s$
with
$T_s$
with
![]() $T_{s+1} \supset T_s$
and
$T_{s+1} \supset T_s$
and
![]() $\sigma \in T$
iff
$\sigma \in T$
iff
![]() $\sigma \in T_{\left \ulcorner \sigma \right \urcorner }$
. We will also maintain a stagewise approximation
$\sigma \in T_{\left \ulcorner \sigma \right \urcorner }$
. We will also maintain a stagewise approximation
![]() $\hat {T}_{s}$
to
$\hat {T}_{s}$
to
![]() $\hat {T}$
. We will organize the construction of by drawing on ideas from
$\hat {T}$
. We will organize the construction of by drawing on ideas from
![]() $\prod ^0_{2}$
constructions in the r.e. sets. In particularly, we will arrange modules on a priority tree, denoted
$\prod ^0_{2}$
constructions in the r.e. sets. In particularly, we will arrange modules on a priority tree, denoted
![]() $ \mathbb {T} \subset \omega ^{<\omega }$
, but the differences between constructing a set and a tree require we make some modifications.
$ \mathbb {T} \subset \omega ^{<\omega }$
, but the differences between constructing a set and a tree require we make some modifications.
Usually, in a
![]() $\prod ^0_{2}$
tree construction we assign modules to elements of
$\prod ^0_{2}$
tree construction we assign modules to elements of
![]() $\omega ^{<\omega }$
, denoting an arbitrary module assigned to
$\omega ^{<\omega }$
, denoting an arbitrary module assigned to
![]() $\alpha $
by
$\alpha $
by
![]() ${\mathcal {M}}_{\alpha }$
(for a module of type R,
${\mathcal {M}}_{\alpha }$
(for a module of type R,
![]() ${\mathcal {R}}_{\alpha }$
) and use only the outcome of that module at stage s to determine where next to visit at stage s. However, rather than working on meeting a requirement globally for the entire tree T we will assign modules to work on meeting a requirement for the path extending
${\mathcal {R}}_{\alpha }$
) and use only the outcome of that module at stage s to determine where next to visit at stage s. However, rather than working on meeting a requirement globally for the entire tree T we will assign modules to work on meeting a requirement for the path extending
![]() $\hat {T}(\sigma )$
for some
$\hat {T}(\sigma )$
for some
![]() $\sigma $
. Thus, rather than working on
$\sigma $
. Thus, rather than working on
![]() $\mathbb {T} \subset \omega ^{<\omega }$
we work on
$\mathbb {T} \subset \omega ^{<\omega }$
we work on
![]() $\mathbb {T} \subset \omega ^{<\omega } \times \omega ^{<\omega }$
. More specifically, we identify modules in our construction with pairs
$\mathbb {T} \subset \omega ^{<\omega } \times \omega ^{<\omega }$
. More specifically, we identify modules in our construction with pairs
![]() $(\alpha , \sigma )$
where
$(\alpha , \sigma )$
where
![]() $\alpha $
is the string built up out of the outcomes of prior modules and
$\alpha $
is the string built up out of the outcomes of prior modules and
![]() $\sigma $
indicates the element in
$\sigma $
indicates the element in
![]() $\mathrm {dom} \hat {T}$
we are working to define. The idea is that at certain points in our construction, rather than following a single outcome of a module, we will simultaneously work both above (our approximation to)
$\mathrm {dom} \hat {T}$
we are working to define. The idea is that at certain points in our construction, rather than following a single outcome of a module, we will simultaneously work both above (our approximation to)
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
and above/to define
$\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
and above/to define
![]() $ \hat {T}(\sigma \widehat {\phantom {x}}\langle m'\rangle )$
.
$ \hat {T}(\sigma \widehat {\phantom {x}}\langle m'\rangle )$
.
When we specify a module
![]() ${\mathcal {M}}_{\xi }$
we also specify a set
${\mathcal {M}}_{\xi }$
we also specify a set
![]() $\mathfrak {O}(\xi )$
of pairs of potential successors
$\mathfrak {O}(\xi )$
of pairs of potential successors
![]() $(o, \delta )$
where o is a potential outcome of the module (identified with elements in
$(o, \delta )$
where o is a potential outcome of the module (identified with elements in
![]() $\omega $
but written more suggestively) and
$\omega $
but written more suggestively) and
![]() $\delta \in \omega ^{<\omega }$
. As usual, at each stage any module we visit will have a single outcome o but as there may be multiple pairs
$\delta \in \omega ^{<\omega }$
. As usual, at each stage any module we visit will have a single outcome o but as there may be multiple pairs
![]() $(o, \delta ) \in \mathfrak {O}(\xi )$
there may be multiple immediate successors of this module which both get visited at this stage. In our construction most modules will only allow
$(o, \delta ) \in \mathfrak {O}(\xi )$
there may be multiple immediate successors of this module which both get visited at this stage. In our construction most modules will only allow
![]() $\delta = \langle \rangle $
but some modules will have successors both of the form
$\delta = \langle \rangle $
but some modules will have successors both of the form
![]() $(o, \langle \rangle )$
and
$(o, \langle \rangle )$
and
![]() $(o, \langle n\rangle )$
(for some particular value n). Thus, we will only work on finitely many modules at any stage. With this in mind, we define our priority tree
$(o, \langle n\rangle )$
(for some particular value n). Thus, we will only work on finitely many modules at any stage. With this in mind, we define our priority tree
![]() $\mathbb {T}$
inductively as follows. In what follows, keep in mind that
$\mathbb {T}$
inductively as follows. In what follows, keep in mind that
![]() ${\left ({\langle a,b\rangle }\right )_{0}} = a$
and
${\left ({\langle a,b\rangle }\right )_{0}} = a$
and
![]() ${\left ({\langle a,b\rangle }\right )_{1}} = b$
.
${\left ({\langle a,b\rangle }\right )_{1}} = b$
.
Definition 6.2.
![]() $\mathbb {T}$
is the smallest set of pairs
$\mathbb {T}$
is the smallest set of pairs
![]() $\langle \alpha ,\sigma \rangle $
closed under the following conditions:
$\langle \alpha ,\sigma \rangle $
closed under the following conditions:
-
•
 $\langle \langle \rangle ,\langle \rangle \rangle \in \mathbb {T}$
.
$\langle \langle \rangle ,\langle \rangle \rangle \in \mathbb {T}$
. -
• If
 $\xi = \langle \alpha ,\sigma \rangle \in \mathbb {T} \land (o, \delta ) \in \mathfrak {O}(\xi )$
then
$\xi = \langle \alpha ,\sigma \rangle \in \mathbb {T} \land (o, \delta ) \in \mathfrak {O}(\xi )$
then
 $\nu = \langle \alpha \widehat {\phantom {x}}\langle o\rangle , \sigma \widehat {\phantom {x}} \delta \rangle \in \mathbb {T}$
. In this case we write
$\nu = \langle \alpha \widehat {\phantom {x}}\langle o\rangle , \sigma \widehat {\phantom {x}} \delta \rangle \in \mathbb {T}$
. In this case we write
 $\nu ^{-} = \xi $
and call
$\nu ^{-} = \xi $
and call
 $\xi $
the predecessor of
$\xi $
the predecessor of
 $\nu $
.
$\nu $
.
We define
![]() $\left \lvert \xi \right \rvert \in \mathbb {T} = \left \lvert {\left ({\xi }\right )_{{0}}} \right \rvert $
and say
$\left \lvert \xi \right \rvert \in \mathbb {T} = \left \lvert {\left ({\xi }\right )_{{0}}} \right \rvert $
and say
![]() $\xi \prec \xi '$
if
$\xi \prec \xi '$
if
![]() $\prec $
holds on both components (i.e.,
$\prec $
holds on both components (i.e.,
![]() ${\left ({\xi }\right )_{i}} \prec {\left ({\xi '}\right )_{i}}, i \in {\left \{{0,1}\right \}}$
). Finally,
${\left ({\xi }\right )_{i}} \prec {\left ({\xi '}\right )_{i}}, i \in {\left \{{0,1}\right \}}$
). Finally,
![]() $\xi ^{-}$
is defined to be the unique
$\xi ^{-}$
is defined to be the unique
![]() $\prec $
maximal element in
$\prec $
maximal element in
![]() $\mathbb {T}$
with
$\mathbb {T}$
with
![]() $\xi ^{-} \prec \xi $
.
$\xi ^{-} \prec \xi $
.
The careful reader might note the possibility that
![]() $\xi ^{-}$
could fail to be unique if we aren’t careful. To avoid this, we assume that the outcomes of
$\xi ^{-}$
could fail to be unique if we aren’t careful. To avoid this, we assume that the outcomes of
![]() $\xi = \langle \alpha ,\sigma \rangle $
are modified to be of the form
$\xi = \langle \alpha ,\sigma \rangle $
are modified to be of the form
![]() $ \langle o,\sigma \rangle $
. This ensures that
$ \langle o,\sigma \rangle $
. This ensures that
![]() $\xi ^{-}$
is uniquely defined and
$\xi ^{-}$
is uniquely defined and
![]() $\prec $
is always a linear order when restricted to the predecessors of
$\prec $
is always a linear order when restricted to the predecessors of
![]() $\xi $
on
$\xi $
on
![]() $\mathbb {T}$
. As it won’t cause any confusion, we will assume this happens in the background and will present our outcomes untransformed.
$\mathbb {T}$
. As it won’t cause any confusion, we will assume this happens in the background and will present our outcomes untransformed.
We now define what it means for a node on this tree to be to the left of another node (we retain the terminology ‘left of’ even though its not longer visually accurate) and extend this to a set of nodes as follows.
Definition 6.3. We define
![]() $\xi <_L \xi '$
on
$\xi <_L \xi '$
on
![]() $\mathbb {T}$
just if there are
$\mathbb {T}$
just if there are
![]() $\nu \prec \xi , \nu ' \prec \xi $
with
$\nu \prec \xi , \nu ' \prec \xi $
with
![]() ${\nu ^{-} = {\nu '}^{-}}$
,
${\nu ^{-} = {\nu '}^{-}}$
,
![]() ${\left (\nu \right )_{0}} = \alpha \widehat {\phantom {x}}\langle o\rangle , {\left ({\nu '}\right )_{0}} = \alpha \widehat {\phantom {x}}\langle o'\rangle $
and
${\left (\nu \right )_{0}} = \alpha \widehat {\phantom {x}}\langle o\rangle , {\left ({\nu '}\right )_{0}} = \alpha \widehat {\phantom {x}}\langle o'\rangle $
and
![]() $o < o'$
. We extend this relation to sets by setting
$o < o'$
. We extend this relation to sets by setting
![]() $Q <_L \xi $
(read left of) for
$Q <_L \xi $
(read left of) for
![]() $Q \subset \mathbb {T}, \xi \in \mathbb {T}$
just if Q contains an element
$Q \subset \mathbb {T}, \xi \in \mathbb {T}$
just if Q contains an element
![]() $\nu <_L \xi $
.
$\nu <_L \xi $
.
Our truepath, and its approximations, will no longer be single paths but sets of nodes. Informally speaking, we define ![]() to be the set of nodes visited at stage s following the rules described above but not visiting any extensions of a node
to be the set of nodes visited at stage s following the rules described above but not visiting any extensions of a node
![]() $\xi $
being visited for the first time at stage s. Formally speaking, we give the following definition.
$\xi $
being visited for the first time at stage s. Formally speaking, we give the following definition.
Definition 6.4. We define ![]() as the largest set satisfying the following closure conditions:
as the largest set satisfying the following closure conditions:
-
•
 .
. -
• If
 ,
,
 $s_\xi> 0$
and at stage s, o is the outcome of
$s_\xi> 0$
and at stage s, o is the outcome of
 $\xi $
at stage s and
$\xi $
at stage s and
 $\nu \in \mathbb {T}, \nu ^{-} = \xi $
with
$\nu \in \mathbb {T}, \nu ^{-} = \xi $
with
 ${\left (\nu \right )_{0}} = {\left (\xi \right )_{0}}\widehat {\phantom {x}}\langle o\rangle $
then
${\left (\nu \right )_{0}} = {\left (\xi \right )_{0}}\widehat {\phantom {x}}\langle o\rangle $
then
 $\nu \in \mathbb {T}$
.
$\nu \in \mathbb {T}$
.
Where
![]() $s_\xi $
is defined to be
$s_\xi $
is defined to be ![]() .
.
We define ![]() iff
iff ![]() .
.
Note that our priority construction will never reinitialize any nodes. That is, our construction will satisfy the following condition.
Condition 1. If
![]() $s'> s$
and
$s'> s$
and ![]() then for all
then for all
![]() $t \geq s'$
$t \geq s'$
![]() .
.
With the action of the priority tree defined we need to specify how the modules are able to control the construction. As described above, modules will directly enumerate elements into
![]() $T = \bigcup _{s \in \omega } T_s$
with a deadline of stage
$T = \bigcup _{s \in \omega } T_s$
with a deadline of stage
![]() $s = \left \ulcorner \sigma \right \urcorner $
to place
$s = \left \ulcorner \sigma \right \urcorner $
to place
![]() $\sigma $
into T. We use a bit more machinery to specify our approximation to
$\sigma $
into T. We use a bit more machinery to specify our approximation to
![]() $\hat {T}$
. Each module
$\hat {T}$
. Each module
![]() ${\mathcal {M}}_{\xi }$
receives a string
${\mathcal {M}}_{\xi }$
receives a string
![]() $\delta ^{\xi }$
and specifies a string
$\delta ^{\xi }$
and specifies a string
![]() $\delta ^{\nu }$
for each successor to
$\delta ^{\nu }$
for each successor to
![]() $\xi $
. If
$\xi $
. If
![]() $\xi = \langle \alpha ,\sigma \rangle $
then we understand the module
$\xi = \langle \alpha ,\sigma \rangle $
then we understand the module
![]() $\xi $
to be executing on the guess that
$\xi $
to be executing on the guess that
![]() $\delta ^{\xi } \prec \hat {T}(\sigma )$
.
$\delta ^{\xi } \prec \hat {T}(\sigma )$
.
This is sufficient for modules that only need to manipulate a single path but some modules will need to manipulate the collection of potential branches of
![]() $\hat {T}(\sigma )$
. To this end, some modules will also define an infinite set
$\hat {T}(\sigma )$
. To this end, some modules will also define an infinite set
![]() $\Theta ^{\xi }$
of branches with the n-th element (ordered lexicographically) indicated by
$\Theta ^{\xi }$
of branches with the n-th element (ordered lexicographically) indicated by
![]() ${\theta ^{\xi }_{n}}$
. In our construction, we will ensure that our definition of
${\theta ^{\xi }_{n}}$
. In our construction, we will ensure that our definition of
![]() $\delta ^{\xi }$
and
$\delta ^{\xi }$
and
![]() $\Theta ^{\xi }$
satisfy the following condition.
$\Theta ^{\xi }$
satisfy the following condition.
Condition 2. For each
![]() $\xi \in \mathbb {T}$
:
$\xi \in \mathbb {T}$
:
-
1. If
 then
then
 ${\mathcal {M}}_{\xi ^{-}}$
must set
${\mathcal {M}}_{\xi ^{-}}$
must set
 $\delta ^{\xi }$
during stage s and ensure
$\delta ^{\xi }$
during stage s and ensure
 $\delta ^{\xi } \in T_{s+1}$
.
$\delta ^{\xi } \in T_{s+1}$
. -
2.
 $\nu \succeq \xi \implies \delta ^{\xi } \succeq \delta ^{\nu }$
.
$\nu \succeq \xi \implies \delta ^{\xi } \succeq \delta ^{\nu }$
.
If
![]() $\xi \in \mathbb {T}$
and
$\xi \in \mathbb {T}$
and
![]() ${\mathcal {M}}_{\xi ^{-}}$
defines
${\mathcal {M}}_{\xi ^{-}}$
defines
![]() $\Theta ^{\xi }$
then:
$\Theta ^{\xi }$
then:
-
1.
 ${\theta ^{\xi }_{n}}$
enumerates
${\theta ^{\xi }_{n}}$
enumerates
 $\Theta ^{\xi }$
with
$\Theta ^{\xi }$
with
 ${\theta ^{\xi }_{n}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k_n\rangle $
with
${\theta ^{\xi }_{n}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k_n\rangle $
with
 $n \mapsto k_n$
monotonic, injective function of n.
$n \mapsto k_n$
monotonic, injective function of n. -
2. If
 then
then
 ${\mathcal {M}}_{\xi ^{-}}$
must set
${\mathcal {M}}_{\xi ^{-}}$
must set
 ${\theta ^{\xi }_{n}}$
by the end of stage s and ensure
${\theta ^{\xi }_{n}}$
by the end of stage s and ensure
 ${\theta ^{\xi }_{n}} \in T_{s+1}$
.
${\theta ^{\xi }_{n}} \in T_{s+1}$
.
These are mostly straightforward demands that what the module at
![]() $\xi $
does is compatible with what
$\xi $
does is compatible with what
![]() $\xi ^{-}$
does and defines its output promptly. However, a few points deserve mentioning. The requirement that
$\xi ^{-}$
does and defines its output promptly. However, a few points deserve mentioning. The requirement that
![]() $ \delta ^{\xi } \in T_{s+1}$
will ensure that
$ \delta ^{\xi } \in T_{s+1}$
will ensure that
![]() $\mathrm {rng} \hat {T} \subset T$
. The final condition will enable multiple modules who all want to ensure the leftmost branch extending
$\mathrm {rng} \hat {T} \subset T$
. The final condition will enable multiple modules who all want to ensure the leftmost branch extending
![]() $\hat {T}(\sigma )$
has some property to cooperate. Without this condition, a module that only ensured
$\hat {T}(\sigma )$
has some property to cooperate. Without this condition, a module that only ensured
![]() ${\theta ^{\xi }_{0}}$
has some property might find their work erased by the next module leaving all extensions of
${\theta ^{\xi }_{0}}$
has some property might find their work erased by the next module leaving all extensions of
![]() ${\theta ^{\xi }_{0}}$
out of the set of branches it specifies.
${\theta ^{\xi }_{0}}$
out of the set of branches it specifies.
We also impose the following condition on the construction to (help) ensure that if ![]() then the modules above
then the modules above
![]() $\xi $
get to control whether
$\xi $
get to control whether
![]() $\delta ^{\xi }$
extends to a path through T.
$\delta ^{\xi }$
extends to a path through T.
Condition 3. If
![]() $\delta ^{\xi } = \tau $
and the module
$\delta ^{\xi } = \tau $
and the module
![]() ${\mathcal {M}}_{\xi }$
enumerates
${\mathcal {M}}_{\xi }$
enumerates
![]() $\sigma $
into T then
$\sigma $
into T then
![]() $\sigma \succ \tau $
.
$\sigma \succ \tau $
.
6.2 Requirements
With an understanding of how our
![]() $\mathbb {T}$
operates we are now in a position to present the requirements our construction will meet and arrange the modules we will use to meet them on the tree. Recall that we seek to prove the following result.
$\mathbb {T}$
operates we are now in a position to present the requirements our construction will meet and arrange the modules we will use to meet them on the tree. Recall that we seek to prove the following result.
Proposition 4.1. Given a (potentially partial) tree
![]() $S \subset \omega ^{<\omega }$
computable in
$S \subset \omega ^{<\omega }$
computable in
![]() ${X}^{\prime \prime }$
there is a (total) computable tree
${X}^{\prime \prime }$
there is a (total) computable tree
![]() $T \subset \omega ^{<\omega }$
and an
$T \subset \omega ^{<\omega }$
and an
![]() ${X}^{\prime \prime }$
computable partial f-tree
${X}^{\prime \prime }$
computable partial f-tree
![]() $\hat {T}$
such that:
$\hat {T}$
such that:
-
1.
 $\mathrm {rng} \hat {T} \subset T$
and
$\mathrm {rng} \hat {T} \subset T$
and
 $[\hat {T}] = [T]$
.
$[\hat {T}] = [T]$
. -
2.
 $\hat {T}(\cdot )$
is a homeomorphism of
$\hat {T}(\cdot )$
is a homeomorphism of
 $[S]$
with
$[S]$
with
 $[T]$
.
$[T]$
. -
3. If
 $f \in [T]$
then
$f \in [T]$
then
 $f \nleq _{\mathbf {T}} X$
.
$f \nleq _{\mathbf {T}} X$
. -
4. If
 $g \in [S]$
then
$g \in [S]$
then
 $g \oplus {X}^{\prime \prime } \equiv _{\mathbf {T}} {\left (\hat {T}(g) \oplus X\right )}^{\prime \prime } \equiv _{\mathbf {T}} \hat {T}(g) \oplus {X}^{\prime \prime }$
.
$g \oplus {X}^{\prime \prime } \equiv _{\mathbf {T}} {\left (\hat {T}(g) \oplus X\right )}^{\prime \prime } \equiv _{\mathbf {T}} \hat {T}(g) \oplus {X}^{\prime \prime }$
. -
5. If
 $f \in [T]$
and
$f \in [T]$
and
 $Y \leq _{\mathbf {T}} f \oplus X$
then either
$Y \leq _{\mathbf {T}} f \oplus X$
then either
 $Y \leq _{\mathbf {T}} X$
or
$Y \leq _{\mathbf {T}} X$
or
 $f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
.
$f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
. -
6. For all
 $\sigma \in 2^{<\omega }$
,
$\sigma \in 2^{<\omega }$
,
 $\left \lvert \hat {T}(\sigma )\right \rvert \geq \lvert \sigma \rvert $
(when defined).
$\left \lvert \hat {T}(\sigma )\right \rvert \geq \lvert \sigma \rvert $
(when defined).
Moreover, this holds with all possible uniformity. In particular, given a computable functional
![]() $\Upsilon _2$
we can effectively produce functionals
$\Upsilon _2$
we can effectively produce functionals
![]() $\Upsilon , \hat {\Upsilon }$
so that whenever
$\Upsilon , \hat {\Upsilon }$
so that whenever
![]() ${\Upsilon _2({X}^{\prime \prime }) =S}$
then
${\Upsilon _2({X}^{\prime \prime }) =S}$
then
![]() $\Upsilon (X)=T$
and
$\Upsilon (X)=T$
and
![]() $\hat {\Upsilon }({X}^{\prime \prime }) = \hat {T}$
with the properties described above.
$\hat {\Upsilon }({X}^{\prime \prime }) = \hat {T}$
with the properties described above.
We work to meet the following requirements during the construction. We state the requirements in unrelativized form. Unlike requirements in the construction of a single set, we work to ensure that the requirement of the form
![]() ${\mathscr {R}}_{e}$
is satisfied for all e and all
${\mathscr {R}}_{e}$
is satisfied for all e and all
![]() $\sigma \in {S^{\langle \infty \rangle }}$
with
$\sigma \in {S^{\langle \infty \rangle }}$
with
![]() $\lvert \sigma \rvert = e$
. For the purposes of stating the requirements, we use
$\lvert \sigma \rvert = e$
. For the purposes of stating the requirements, we use
![]() $\hat {T}^-(\sigma )$
to denote an extension of
$\hat {T}^-(\sigma )$
to denote an extension of
![]() $ \hat {T}(\sigma ^{-})$
that would be extended by
$ \hat {T}(\sigma ^{-})$
that would be extended by
![]() $\hat {T}(\sigma )$
if the later were defined. We won’t actually define this function but just use it in the requirements to stand in for some string to be defined later.Footnote
5
$\hat {T}(\sigma )$
if the later were defined. We won’t actually define this function but just use it in the requirements to stand in for some string to be defined later.Footnote
5
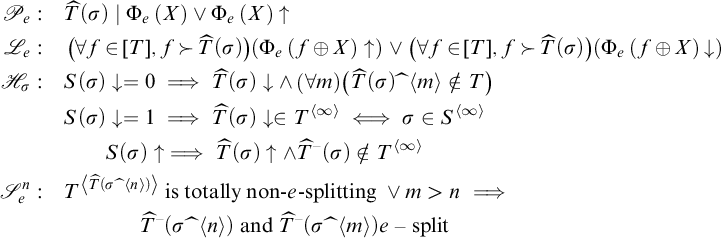 $$ \begin{align*} {\mathscr{P}}_{e}:\quad &\hat{T}(\sigma) \mid \Phi_{e}\left(X\right) \lor \Phi_{e}\left(X\right)\uparrow\\ {\mathscr{L}}_{e}:\quad & \left(\forall {f \kern1.3pt{\in}\kern1.3pt [T], f \kern1.2pt{\succ}\kern1.2pt \hat{T}(\sigma)}\right)\!\left(\Phi_{e}\left(f \kern1.2pt{\oplus}\kern1.2pt X\right)\uparrow\right) \kern1.2pt{\lor}\kern1.2pt \left(\forall {f \kern1.2pt{\in}\kern1.2pt [T], f \kern1.3pt{\succ}\kern1.3pt \hat{T}(\sigma)}\right)\!\left(\Phi_{e}\left(f \kern1.3pt{\oplus}\kern1.3pt X\right)\kern-1pt\downarrow\right)\\{\mathscr{H}}_{\sigma}:\quad& S(\sigma)\downarrow = 0 \implies \hat{T}(\sigma)\downarrow \land \left(\forall m\right)\!\left(\hat{T}(\sigma)\widehat{\phantom{x}}\langle m\rangle \notin T \right) \\ &S(\sigma)\downarrow = 1 \implies \hat{T}(\sigma)\downarrow \in {T^{\langle \infty\rangle}} \iff \sigma \in {S^{\langle\infty\rangle}} \\ &\qquad S(\sigma)\uparrow \implies \hat{T}(\sigma)\uparrow \land \hat{T}^-(\sigma) \notin {T^{\langle\infty\rangle}}\\{\mathscr{S}}^n_{e}:\quad& T^{\left\langle \hat{T}(\sigma\widehat{\phantom{x}}\langle n\rangle) \right\rangle} \text{ is totally non-}e\text{-splitting } \lor m> n \implies \\ &\qquad\qquad\!\!\hat{T}^-(\sigma\widehat{\phantom{x}}\langle n\rangle) \text{ and } \hat{T}^-(\sigma\widehat{\phantom{x}}\langle m\rangle) e-\text{split} \end{align*} $$
$$ \begin{align*} {\mathscr{P}}_{e}:\quad &\hat{T}(\sigma) \mid \Phi_{e}\left(X\right) \lor \Phi_{e}\left(X\right)\uparrow\\ {\mathscr{L}}_{e}:\quad & \left(\forall {f \kern1.3pt{\in}\kern1.3pt [T], f \kern1.2pt{\succ}\kern1.2pt \hat{T}(\sigma)}\right)\!\left(\Phi_{e}\left(f \kern1.2pt{\oplus}\kern1.2pt X\right)\uparrow\right) \kern1.2pt{\lor}\kern1.2pt \left(\forall {f \kern1.2pt{\in}\kern1.2pt [T], f \kern1.3pt{\succ}\kern1.3pt \hat{T}(\sigma)}\right)\!\left(\Phi_{e}\left(f \kern1.3pt{\oplus}\kern1.3pt X\right)\kern-1pt\downarrow\right)\\{\mathscr{H}}_{\sigma}:\quad& S(\sigma)\downarrow = 0 \implies \hat{T}(\sigma)\downarrow \land \left(\forall m\right)\!\left(\hat{T}(\sigma)\widehat{\phantom{x}}\langle m\rangle \notin T \right) \\ &S(\sigma)\downarrow = 1 \implies \hat{T}(\sigma)\downarrow \in {T^{\langle \infty\rangle}} \iff \sigma \in {S^{\langle\infty\rangle}} \\ &\qquad S(\sigma)\uparrow \implies \hat{T}(\sigma)\uparrow \land \hat{T}^-(\sigma) \notin {T^{\langle\infty\rangle}}\\{\mathscr{S}}^n_{e}:\quad& T^{\left\langle \hat{T}(\sigma\widehat{\phantom{x}}\langle n\rangle) \right\rangle} \text{ is totally non-}e\text{-splitting } \lor m> n \implies \\ &\qquad\qquad\!\!\hat{T}^-(\sigma\widehat{\phantom{x}}\langle n\rangle) \text{ and } \hat{T}^-(\sigma\widehat{\phantom{x}}\langle m\rangle) e-\text{split} \end{align*} $$
Note that
![]() $\Phi _{e}\left (f\right )\downarrow $
means
$\Phi _{e}\left (f\right )\downarrow $
means
![]() $\left (\forall n\right )\!\left (\Phi _{e}\left (f;n\right )\downarrow \!\right )$
(and similarly for
$\left (\forall n\right )\!\left (\Phi _{e}\left (f;n\right )\downarrow \!\right )$
(and similarly for
![]() $\Phi _{e}\left (f\right )\uparrow $
) and that, when we speak of e-splittings we mean the notion relativized to X. The statement of
$\Phi _{e}\left (f\right )\uparrow $
) and that, when we speak of e-splittings we mean the notion relativized to X. The statement of
![]() ${\mathscr {H}}_{\sigma }$
is a bit odd in the case where
${\mathscr {H}}_{\sigma }$
is a bit odd in the case where
![]() $\sigma \in S$
since in that we do nothing except don’t try to stop
$\sigma \in S$
since in that we do nothing except don’t try to stop
![]() $\hat {T}(\sigma )$
from potentially extending to a full path should
$\hat {T}(\sigma )$
from potentially extending to a full path should
![]() $\sigma $
extend to a full path through S.
$\sigma $
extend to a full path through S.
Each requirement gets its own module to assist in meeting it; however, some modules get helper modules. For instance, we break up meeting the requirement
![]() ${\mathscr {H}}_{\sigma }$
into a module
${\mathscr {H}}_{\sigma }$
into a module
![]() ${\mathcal {H}}^+_{\sigma ^{-}}$
responsible for creating an
${\mathcal {H}}^+_{\sigma ^{-}}$
responsible for creating an
![]() $\omega $
-branching above
$\omega $
-branching above
![]() $\hat {T}(\sigma ^{-})$
and a module
$\hat {T}(\sigma ^{-})$
and a module
![]() ${\mathcal {H}}_{\sigma }$
responsible for ensuring
${\mathcal {H}}_{\sigma }$
responsible for ensuring
![]() $\hat {T}(\sigma )$
doesn’t extend to a path through T if
$\hat {T}(\sigma )$
doesn’t extend to a path through T if
![]() $\sigma \notin S$
. Similarly, we supplement
$\sigma \notin S$
. Similarly, we supplement
![]() ${\mathcal {L}}_{e}$
with submodules
${\mathcal {L}}_{e}$
with submodules
![]() ${\mathcal {L}}^n_{e}$
responsible for checking if we can extend
${\mathcal {L}}^n_{e}$
responsible for checking if we can extend
![]() $\Phi _{e}\left (f\right )$
to converge on
$\Phi _{e}\left (f\right )$
to converge on
![]() $\Phi _{e}\left (f;n\right )$
. Finally, we use the module
$\Phi _{e}\left (f;n\right )$
. Finally, we use the module
![]() $ {\mathcal {S}}^n_{-1}$
as a helper to split off those modules who will work above
$ {\mathcal {S}}^n_{-1}$
as a helper to split off those modules who will work above
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle n\rangle )$
from those modules working to define
$\hat {T}(\sigma \widehat {\phantom {x}}\langle n\rangle )$
from those modules working to define
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle ), m> n$
.
$\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle ), m> n$
.
Definition 6.5. Modules are be assigned to nodes on
![]() $\mathbb {T}$
as follows:
$\mathbb {T}$
as follows:
-
1. If
 $\xi = (\langle \rangle , \langle \rangle )$
then
$\xi = (\langle \rangle , \langle \rangle )$
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {H}}^+_{\langle \rangle }$
. Also, if
${\mathcal {H}}^+_{\langle \rangle }$
. Also, if
 $\xi ^{-}$
implements some module
$\xi ^{-}$
implements some module
 ${\mathcal {H}}_{\sigma }$
and has an outcome guessing
${\mathcal {H}}_{\sigma }$
and has an outcome guessing
 $\sigma \in S$
then
$\sigma \in S$
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {H}}^+_{\sigma }$
.
${\mathcal {H}}^+_{\sigma }$
. -
2. If
 $\xi ^{-}$
implements
$\xi ^{-}$
implements
 ${\mathcal {H}}^+_{\sigma }$
with
${\mathcal {H}}^+_{\sigma }$
with
 $\lvert \sigma \rvert = e$
then
$\lvert \sigma \rvert = e$
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {S}}^0_{e}$
.
${\mathcal {S}}^0_{e}$
. -
3. If
 $\xi ^{-}$
implements
$\xi ^{-}$
implements
 ${\mathcal {S}}^n_{e}$
with
${\mathcal {S}}^n_{e}$
with
 $e \geq 0$
then
$e \geq 0$
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {S}}^n_{e - 1}$
.
${\mathcal {S}}^n_{e - 1}$
. -
4. If
 $\xi ^{-}$
implements
$\xi ^{-}$
implements
 ${\mathcal {S}}^n_{-1}$
and
${\mathcal {S}}^n_{-1}$
and
 ${\left (\xi \right )_{1}} = {\left ({\xi ^{-}}\right )_{1}} = \sigma $
then
${\left (\xi \right )_{1}} = {\left ({\xi ^{-}}\right )_{1}} = \sigma $
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {S}}^{n+1}_{e}$
where
${\mathcal {S}}^{n+1}_{e}$
where
 $\lvert \sigma \rvert = e$
.
$\lvert \sigma \rvert = e$
. -
5. If
 $\xi ^{-}$
implements
$\xi ^{-}$
implements
 ${\mathcal {S}}^n_{-1}$
and
${\mathcal {S}}^n_{-1}$
and
 ${\left (\xi \right )_{1}} \neq {\left ({\xi ^{-}}\right )_{1}}$
then
${\left (\xi \right )_{1}} \neq {\left ({\xi ^{-}}\right )_{1}}$
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {P}}_{e}$
for the least e such that no module of this form is assigned to any
${\mathcal {P}}_{e}$
for the least e such that no module of this form is assigned to any  .
. -
6. If
 $\xi ^{-}$
implements
$\xi ^{-}$
implements
 ${\mathcal {P}}_{i}$
then
${\mathcal {P}}_{i}$
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {L}}_{e}$
for the least e such that no
${\mathcal {L}}_{e}$
for the least e such that no  implements
implements
 ${\mathcal {L}}_{e}$
.
${\mathcal {L}}_{e}$
. -
7. If
 $\xi ^{-}$
implements a module of the form
$\xi ^{-}$
implements a module of the form
 ${\mathcal {L}}_{e}$
or
${\mathcal {L}}_{e}$
or
 ${\mathcal {L}}^n_{e}$
then let
${\mathcal {L}}^n_{e}$
then let
 $i < e$
(if it exists) be the largest value such that
$i < e$
(if it exists) be the largest value such that
 $\xi $
extends the outcome
$\xi $
extends the outcome
 $\left \ulcorner \downarrow \right \urcorner $
of
$\left \ulcorner \downarrow \right \urcorner $
of
 $ {\mathcal {L}}_{i}$
and m be the least such that no predecessor of
$ {\mathcal {L}}_{i}$
and m be the least such that no predecessor of
 $\xi $
implements
$\xi $
implements
 ${\mathcal {L}}^m_{i}$
then
${\mathcal {L}}^m_{i}$
then
 $\xi $
implements
$\xi $
implements
 ${\mathcal {L}}^m_{i}$
.
${\mathcal {L}}^m_{i}$
. -
8. If
 $\xi ^{-}$
implements a module of the form
$\xi ^{-}$
implements a module of the form
 ${\mathcal {L}}_{e}$
or
${\mathcal {L}}_{e}$
or
 ${\mathcal {L}}^n_{e}$
and either
${\mathcal {L}}^n_{e}$
and either
 $e = 0$
or for all
$e = 0$
or for all
 $i < e$
$i < e$
 $\xi ^{-}$
doesn’t extend the
$\xi ^{-}$
doesn’t extend the
 $\left \ulcorner \downarrow \right \urcorner $
outcome of
$\left \ulcorner \downarrow \right \urcorner $
outcome of
 ${\mathcal {L}}_{i}$
and
${\mathcal {L}}_{i}$
and
 $\sigma = {\left ({\xi }\right )_{1}}$
then
$\sigma = {\left ({\xi }\right )_{1}}$
then
 $\xi $
implements the module
$\xi $
implements the module
 ${\mathcal {H}}_{\sigma }$
${\mathcal {H}}_{\sigma }$
Before we get into any further details, we give a high-level overview of how this is all supposed to work. If we suppose that we’ve just defined
![]() $\hat {T}(\sigma )$
and wish to define
$\hat {T}(\sigma )$
and wish to define
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
we start with the module
$\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
we start with the module
![]() ${\mathcal {H}}^+_{\sigma }$
which will specify a bunch of immediate extensions of
${\mathcal {H}}^+_{\sigma }$
which will specify a bunch of immediate extensions of
![]() $\hat {T}(\sigma )$
(placing them in T). We start by executing
$\hat {T}(\sigma )$
(placing them in T). We start by executing
![]() ${\mathcal {S}}^0_{e}, \lvert \sigma \rvert = e$
then
${\mathcal {S}}^0_{e}, \lvert \sigma \rvert = e$
then
![]() ${\mathcal {S}}^0_{e -1 }$
and so forth all of which work to ensure the leftmost potential extension of
${\mathcal {S}}^0_{e -1 }$
and so forth all of which work to ensure the leftmost potential extension of
![]() $\hat {T}(\sigma )$
e-split or
$\hat {T}(\sigma )$
e-split or
![]() $e -1$
split or so on with all the remaining potential extensions. When we finally get to the module
$e -1$
split or so on with all the remaining potential extensions. When we finally get to the module
![]() $ {\mathcal {S}}^0_{-1}$
it specifies that
$ {\mathcal {S}}^0_{-1}$
it specifies that
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
extends the leftmost branch as extended by all the modules
$\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
extends the leftmost branch as extended by all the modules
![]() ${\mathcal {S}}^0_{e'}, e' \leq e$
and the construction now splits into one part which works on the next module
${\mathcal {S}}^0_{e'}, e' \leq e$
and the construction now splits into one part which works on the next module
![]() ${\mathcal {P}}_{e}$
along that path specified as an initial segment of
${\mathcal {P}}_{e}$
along that path specified as an initial segment of
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
and another part where
$\hat {T}(\sigma \widehat {\phantom {x}}\langle 0\rangle )$
and another part where
![]() ${\mathcal {S}}^1_e$
starts working to define the node which will be extended by
${\mathcal {S}}^1_e$
starts working to define the node which will be extended by
![]() $ \hat {T}(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
. After the module of the form
$ \hat {T}(\sigma \widehat {\phantom {x}}\langle 1\rangle )$
. After the module of the form
![]() ${\mathcal {P}}_{e}$
we work on the next module of the form
${\mathcal {P}}_{e}$
we work on the next module of the form
![]() ${\mathcal {L}}_{e}$
and then, if we are above the total outcome any
${\mathcal {L}}_{e}$
and then, if we are above the total outcome any
![]() ${\mathcal {L}}_{e'}, e' \leq e$
we implement the next helper module of the form
${\mathcal {L}}_{e'}, e' \leq e$
we implement the next helper module of the form
![]() ${\mathcal {L}}^m_{e'}$
. Finally, after those modules, comes the module
${\mathcal {L}}^m_{e'}$
. Finally, after those modules, comes the module
![]() ${\mathcal {H}}_{\sigma \widehat {\phantom {x}}\langle m\rangle }$
(assuming we took the path working on
${\mathcal {H}}_{\sigma \widehat {\phantom {x}}\langle m\rangle }$
(assuming we took the path working on
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
) which guesses whether or not
$\hat {T}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
) which guesses whether or not
![]() $\sigma \widehat {\phantom {x}}\langle m\rangle \in S$
. If it determines
$\sigma \widehat {\phantom {x}}\langle m\rangle \in S$
. If it determines
![]() $\sigma \widehat {\phantom {x}}\langle m\rangle $
is in S then we go on to
$\sigma \widehat {\phantom {x}}\langle m\rangle $
is in S then we go on to
![]() ${\mathcal {H}}^+_{\sigma \widehat {\phantom {x}}\langle m\rangle }$
. If it determines that
${\mathcal {H}}^+_{\sigma \widehat {\phantom {x}}\langle m\rangle }$
. If it determines that
![]() $\sigma \widehat {\phantom {x}}\langle m\rangle $
is not in S then no module is assigned above that outcome preventing any path from being constructed.
$\sigma \widehat {\phantom {x}}\langle m\rangle $
is not in S then no module is assigned above that outcome preventing any path from being constructed.
With this in mind, we can now give a formal definition of
![]() $\hat {T}$
and its stagewise approximation.
$\hat {T}$
and its stagewise approximation.
Definition 6.6. We define
![]() $\hat {T}_{s}(\sigma ) = \delta ^{\xi }$
where
$\hat {T}_{s}(\sigma ) = \delta ^{\xi }$
where ![]() and
and
![]() $\xi ^{-}$
implements the module
$\xi ^{-}$
implements the module
![]() ${\mathcal {H}}_{\sigma }$
. If no such
${\mathcal {H}}_{\sigma }$
. If no such ![]() then it is undefined. We define
then it is undefined. We define
![]() $ \hat {T}(\sigma )$
) in a similar manner except we require that
$ \hat {T}(\sigma )$
) in a similar manner except we require that ![]() .
.
6.3 Modules
We now describe the operation of the modules. For this subsection, we describe the operation of the module assuming it is located at the node
![]() $\xi \in \mathbb {T}, \xi = (\alpha , \sigma )$
and executing at stage s. As we only define the outcome of the module at
$\xi \in \mathbb {T}, \xi = (\alpha , \sigma )$
and executing at stage s. As we only define the outcome of the module at
![]() $\xi $
when
$\xi $
when
![]() $s_\xi> 0$
we understand the previous outcome of the module to be undefined when
$s_\xi> 0$
we understand the previous outcome of the module to be undefined when
![]() $s_\xi \leq 1$
.
$s_\xi \leq 1$
.
6.3.1 Module
 ${ \mathcal {P}}_{e}$
.
${ \mathcal {P}}_{e}$
.
The module
![]() ${\mathcal {P}}_{e}$
has outcomes
${\mathcal {P}}_{e}$
has outcomes
![]() $\left \ulcorner \neq \right \urcorner <_L \left \ulcorner \uparrow \right \urcorner $
and
$\left \ulcorner \neq \right \urcorner <_L \left \ulcorner \uparrow \right \urcorner $
and
![]() $(o, \delta ) \in \mathfrak {O}(\xi )$
iff
$(o, \delta ) \in \mathfrak {O}(\xi )$
iff
![]() $\delta = \langle \rangle $
and o is one of the above two outcomes.
$\delta = \langle \rangle $
and o is one of the above two outcomes.
If the previous outcome was
![]() $\left \ulcorner \neq \right \urcorner $
we retain that outcome. Otherwise, the module acts as follows.
$\left \ulcorner \neq \right \urcorner $
we retain that outcome. Otherwise, the module acts as follows.
Check if there is any
![]() $\tau \in T_s, \tau \succ \delta ^{\xi }$
with
$\tau \in T_s, \tau \succ \delta ^{\xi }$
with
![]() $\Phi _{e,s}\left (X\right ) \mid \tau $
. If found set the outcome to
$\Phi _{e,s}\left (X\right ) \mid \tau $
. If found set the outcome to
![]() $\left \ulcorner \neq \right \urcorner $
and
$\left \ulcorner \neq \right \urcorner $
and
![]() $\delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \neq \right \urcorner \rangle , \sigma \rangle }$
to be a
$\delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \neq \right \urcorner \rangle , \sigma \rangle }$
to be a
![]() $\prec $
maximal extension of
$\prec $
maximal extension of
![]() $\tau $
in
$\tau $
in
![]() $T_s$
. Otherwise, set the outcome to
$T_s$
. Otherwise, set the outcome to
![]() $\left \ulcorner \uparrow \right \urcorner $
and, if this is the first stage at which that outcome is visited, set
$\left \ulcorner \uparrow \right \urcorner $
and, if this is the first stage at which that outcome is visited, set
![]() $ \delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \uparrow \right \urcorner \rangle , \sigma \rangle } = \delta ^{\xi }$
.
$ \delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \uparrow \right \urcorner \rangle , \sigma \rangle } = \delta ^{\xi }$
.
6.3.2 Module
 ${ \mathcal {L}}_{e}$
.
${ \mathcal {L}}_{e}$
.
The module
![]() ${\mathcal {L}}_{e}$
has outcomes
${\mathcal {L}}_{e}$
has outcomes
![]() $\left \ulcorner \downarrow \right \urcorner = 0$
and
$\left \ulcorner \downarrow \right \urcorner = 0$
and
![]() $\left \ulcorner \nu \right \urcorner $
where
$\left \ulcorner \nu \right \urcorner $
where
![]() $\nu \succ \xi $
and some module of the form
$\nu \succ \xi $
and some module of the form
![]() ${\mathcal {L}}^n_{e}$
is assigned to
${\mathcal {L}}^n_{e}$
is assigned to
![]() $\nu $
(hence
$\nu $
(hence
![]() $\left \ulcorner \nu \right \urcorner> 0$
).
$\left \ulcorner \nu \right \urcorner> 0$
).
![]() $ \mathfrak {O}(\xi )$
consists of all pairs
$ \mathfrak {O}(\xi )$
consists of all pairs
![]() $(o, \delta )$
where o is one of the allowed outcomes and
$(o, \delta )$
where o is one of the allowed outcomes and
![]() $\delta = \langle \rangle $
. The outcome
$\delta = \langle \rangle $
. The outcome
![]() $\left \ulcorner \downarrow \right \urcorner $
corresponds to the state where
$\left \ulcorner \downarrow \right \urcorner $
corresponds to the state where
![]() $\Phi _{e}\left (X \oplus f\right )$
is total for all paths
$\Phi _{e}\left (X \oplus f\right )$
is total for all paths
![]() $f \in [T], f \succ \delta ^{\xi }$
and the outcome
$f \in [T], f \succ \delta ^{\xi }$
and the outcome
![]() $\left \ulcorner \nu \right \urcorner $
where
$\left \ulcorner \nu \right \urcorner $
where
![]() $\nu $
implements
$\nu $
implements
![]() ${\mathcal {L}}^n_{e}$
corresponds to the state where all
${\mathcal {L}}^n_{e}$
corresponds to the state where all
![]() $f \in [T], f \succ \delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \nu \right \urcorner \rangle , \sigma \rangle }$
satisfy
$f \in [T], f \succ \delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \nu \right \urcorner \rangle , \sigma \rangle }$
satisfy
![]() $\Phi _{e}\left (X \oplus f;n\right )\uparrow $
.
$\Phi _{e}\left (X \oplus f;n\right )\uparrow $
.
Intuitively, we can think of the operation of
![]() ${\mathcal {L}}^n_{e}$
as creating something of a link with
${\mathcal {L}}^n_{e}$
as creating something of a link with
![]() ${\mathcal {L}}_{e}$
as in a
${\mathcal {L}}_{e}$
as in a
![]() ${\mathbf {0}}^{\prime \prime \prime }$
construction. When we visit
${\mathbf {0}}^{\prime \prime \prime }$
construction. When we visit
![]() ${\mathcal {L}}^n_{e}$
we effectively pause the operation of all the intervening modules between
${\mathcal {L}}^n_{e}$
we effectively pause the operation of all the intervening modules between
![]() ${\mathcal {L}}_{e}$
and
${\mathcal {L}}_{e}$
and
![]() ${\mathcal {L}}^n_{e}$
and start meeting the modules extending
${\mathcal {L}}^n_{e}$
and start meeting the modules extending
![]() ${\mathcal {L}}_{e}$
again until we find an extension which causes the e-th functional to converge on argument n at which point we return to
${\mathcal {L}}_{e}$
again until we find an extension which causes the e-th functional to converge on argument n at which point we return to
![]() ${\mathcal {L}}_{e}$
. Luckily, however, we don’t need the full machinery of links and can achieve this effect merely by letting the module
${\mathcal {L}}_{e}$
. Luckily, however, we don’t need the full machinery of links and can achieve this effect merely by letting the module
![]() $ {\mathcal {L}}^n_{e}$
manipulate the internal state of the unique visiting module
$ {\mathcal {L}}^n_{e}$
manipulate the internal state of the unique visiting module
![]() ${\mathcal {L}}_{e}$
as defined here.
${\mathcal {L}}_{e}$
as defined here.
If
![]() $s_\xi = 0$
we initialize
$s_\xi = 0$
we initialize
![]() $\upsilon = \uparrow , \delta = \uparrow $
. If
$\upsilon = \uparrow , \delta = \uparrow $
. If
![]() $s_\xi> 0$
and
$s_\xi> 0$
and
![]() $\upsilon \uparrow $
then we visit the outcome
$\upsilon \uparrow $
then we visit the outcome
![]() $\left \ulcorner \downarrow \right \urcorner $
with
$\left \ulcorner \downarrow \right \urcorner $
with
![]() $ \delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \downarrow \right \urcorner \rangle , \sigma \rangle } = \delta ^{\xi }$
. We leave it to the submodules of the form
$ \delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \downarrow \right \urcorner \rangle , \sigma \rangle } = \delta ^{\xi }$
. We leave it to the submodules of the form
![]() ${\mathcal {L}}^n_{e}$
to define
${\mathcal {L}}^n_{e}$
to define
![]() $\upsilon , \eta $
when necessary.
$\upsilon , \eta $
when necessary.
If
![]() $s_\xi> 0$
and
$s_\xi> 0$
and
![]() $\upsilon \downarrow $
with
$\upsilon \downarrow $
with
![]() ${\mathcal {L}}^n_{e}$
assigned to
${\mathcal {L}}^n_{e}$
assigned to
![]() $\upsilon $
then we check if there is a (maximal) extension
$\upsilon $
then we check if there is a (maximal) extension
![]() $\tau \succ \delta , \tau \in T_s$
such that
$\tau \succ \delta , \tau \in T_s$
such that
![]() $\Phi _{e}\left (\tau ;n\right )\downarrow $
. If there is, then set
$\Phi _{e}\left (\tau ;n\right )\downarrow $
. If there is, then set
![]() $\delta ^{\upsilon ^{+}} = \tau $
where
$\delta ^{\upsilon ^{+}} = \tau $
where
![]() $\upsilon ^{+}$
is the unique successor of
$\upsilon ^{+}$
is the unique successor of
![]() $\upsilon $
on
$\upsilon $
on
![]() $\mathbb {T}$
, set
$\mathbb {T}$
, set
![]() $\upsilon , \delta $
to be undefined, and visit the outcome
$\upsilon , \delta $
to be undefined, and visit the outcome
![]() $\left \ulcorner \downarrow \right \urcorner $
as above. Otherwise, visit the outcome
$\left \ulcorner \downarrow \right \urcorner $
as above. Otherwise, visit the outcome
![]() $\left \ulcorner \upsilon \right \urcorner $
with
$\left \ulcorner \upsilon \right \urcorner $
with
![]() $\delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \upsilon \right \urcorner \rangle ,\sigma \rangle } = \delta $
.
$\delta ^{\langle \alpha \widehat {\phantom {x}}\langle \left \ulcorner \upsilon \right \urcorner \rangle ,\sigma \rangle } = \delta $
.
6.3.3 Module
 ${ \mathcal {L}}^n_{e}$
.
${ \mathcal {L}}^n_{e}$
.
This node only has a single outcome
![]() $0$
and
$0$
and
![]() $\mathfrak {O}(\xi ) = {\left \{(0, \langle \rangle )\right \}}$
.
$\mathfrak {O}(\xi ) = {\left \{(0, \langle \rangle )\right \}}$
.
Let
![]() $\nu \prec \xi $
be the unique ancestor node implementing
$\nu \prec \xi $
be the unique ancestor node implementing
![]() ${\mathcal {L}}_{e}$
. If
${\mathcal {L}}_{e}$
. If
![]() $s_\xi = 0$
then set the variables
$s_\xi = 0$
then set the variables
![]() $\upsilon , \delta $
for the module at node
$\upsilon , \delta $
for the module at node
![]() $\nu $
to be equal to
$\nu $
to be equal to
![]() $\xi $
and
$\xi $
and
![]() $\delta ^{\xi }$
respectively. If we are ever visited again, we visit our single outcome and rely on the node implementing
$\delta ^{\xi }$
respectively. If we are ever visited again, we visit our single outcome and rely on the node implementing
![]() ${\mathcal {L}}_{e}$
to have set
${\mathcal {L}}_{e}$
to have set
![]() $\delta ^{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle ,\sigma \rangle }$
.
$\delta ^{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle ,\sigma \rangle }$
.
6.3.4 Module
 ${ \mathcal {H}}^+_{\sigma }$
.
${ \mathcal {H}}^+_{\sigma }$
.
This node only has a single outcome
![]() $0$
and
$0$
and
![]() $\mathfrak {O}(\xi ) = {\left \{(0, \langle \rangle )\right \}}$
. Let
$\mathfrak {O}(\xi ) = {\left \{(0, \langle \rangle )\right \}}$
. Let
![]() $\nu = (\alpha \widehat {\phantom {x}}\langle 0\rangle , \sigma )$
and if
$\nu = (\alpha \widehat {\phantom {x}}\langle 0\rangle , \sigma )$
and if
![]() $s_\xi = 1$
then set
$s_\xi = 1$
then set
![]() $\delta ^{\nu }$
to be a maximal element in
$\delta ^{\nu }$
to be a maximal element in
![]() $T_s$
extending
$T_s$
extending
![]() $ \delta ^{\xi }$
. If
$ \delta ^{\xi }$
. If
![]() $s_\xi = n + 1$
(hence
$s_\xi = n + 1$
(hence
![]() $s_\nu = n$
) then let k be large and
$s_\nu = n$
) then let k be large and
![]() $\tau = \delta ^{\nu }\widehat {\phantom {x}}\langle k\rangle $
(in particular, large enough that if
$\tau = \delta ^{\nu }\widehat {\phantom {x}}\langle k\rangle $
(in particular, large enough that if
![]() $\left \ulcorner \tau \right \urcorner> s$
). Enumerate
$\left \ulcorner \tau \right \urcorner> s$
). Enumerate
![]() $\tau $
into
$\tau $
into
![]() $T_{s+1}$
and set
$T_{s+1}$
and set
![]() ${\theta ^{\nu }_{n}} = \tau $
.
${\theta ^{\nu }_{n}} = \tau $
.
6.3.5 Module
 ${ \mathcal {S}}^n_{-1}$
.
${ \mathcal {S}}^n_{-1}$
.
This node only has a single outcome
![]() $0$
, but
$0$
, but
![]() $\mathfrak {O}(\xi ) = {\left \{{(0, {\langle n\rangle }), (0, \langle \rangle )}\right \}}$
. This module doesn’t take any actions, merely split up input it gets between the two successor nodes as follows. Specifically, it sets
$\mathfrak {O}(\xi ) = {\left \{{(0, {\langle n\rangle }), (0, \langle \rangle )}\right \}}$
. This module doesn’t take any actions, merely split up input it gets between the two successor nodes as follows. Specifically, it sets
![]() $\delta ^{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle , \sigma \widehat {\phantom {x}}\langle n\rangle \rangle } = {\theta ^{\xi }_{0}}$
,
$\delta ^{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle , \sigma \widehat {\phantom {x}}\langle n\rangle \rangle } = {\theta ^{\xi }_{0}}$
,
![]() $\delta ^{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle ,\sigma \rangle } = \delta ^{\xi }$
, and
$\delta ^{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle ,\sigma \rangle } = \delta ^{\xi }$
, and
![]() ${\theta ^{{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle ,\sigma \rangle }}_{n}} = {\theta ^{\xi }_{n+1}}$
.
${\theta ^{{\langle \alpha \widehat {\phantom {x}}\langle 0\rangle ,\sigma \rangle }}_{n}} = {\theta ^{\xi }_{n+1}}$
.
6.3.6 Module
 ${ \mathcal {S}}^n_{e}$
.
${ \mathcal {S}}^n_{e}$
.
This node has outcomes
![]() $\left \ulcorner {\,\not |\,}\right \urcorner = 0$
,
$\left \ulcorner {\,\not |\,}\right \urcorner = 0$
,
![]() $\left \ulcorner \mid _0\right \urcorner = 1$
,
$\left \ulcorner \mid _0\right \urcorner = 1$
,
![]() $\left \ulcorner (\mid _1, n)\right \urcorner = 2 + \langle n, 0\rangle $
, and
$\left \ulcorner (\mid _1, n)\right \urcorner = 2 + \langle n, 0\rangle $
, and
![]() $\left \ulcorner (\uparrow ,n,m)\right \urcorner = \langle n, m+1\rangle $
.
$\left \ulcorner (\uparrow ,n,m)\right \urcorner = \langle n, m+1\rangle $
.
![]() $\mathfrak {O}(\xi )$
consists of all pairs
$\mathfrak {O}(\xi )$
consists of all pairs
![]() $ (o, \delta )$
where o is one of the allowed outcomes and
$ (o, \delta )$
where o is one of the allowed outcomes and
![]() $\delta = \langle \rangle $
. Remember that in what follows e-splitting refers to the notion relativized to X.
$\delta = \langle \rangle $
. Remember that in what follows e-splitting refers to the notion relativized to X.
The outcome
![]() $\left \ulcorner {\,\not |\,}\right \urcorner $
corresponds to the case where
$\left \ulcorner {\,\not |\,}\right \urcorner $
corresponds to the case where
![]() ${\theta ^{\xi }_{0}}$
isn’t extended by an e-splitting in T (as
${\theta ^{\xi }_{0}}$
isn’t extended by an e-splitting in T (as
![]() ${\,\not |\,}$
indicates the strings are compatible). The other outcomes presume we do find some e-splitting
${\,\not |\,}$
indicates the strings are compatible). The other outcomes presume we do find some e-splitting
![]() $\tau _0, \tau _1$
extending
$\tau _0, \tau _1$
extending
![]() ${\theta ^{\xi }_{0}}$
. The outcome
${\theta ^{\xi }_{0}}$
. The outcome
![]() $o = \left \ulcorner \mid _0\right \urcorner $
corresponds to the case where we find infinitely many elements in
$o = \left \ulcorner \mid _0\right \urcorner $
corresponds to the case where we find infinitely many elements in
![]() $\Theta ^{\xi }$
that extend to an e-splitting with
$\Theta ^{\xi }$
that extend to an e-splitting with
![]() $\tau _0$
. Outcomes of the form
$\tau _0$
. Outcomes of the form
![]() $\left \ulcorner (\mid _1, n)\right \urcorner $
correspond to the case where we only find n elements in
$\left \ulcorner (\mid _1, n)\right \urcorner $
correspond to the case where we only find n elements in
![]() $\Theta ^{\xi }$
that extend to an e-splitting with
$\Theta ^{\xi }$
that extend to an e-splitting with
![]() $\tau _0$
but infinitely many which extend to an e-splitting with
$\tau _0$
but infinitely many which extend to an e-splitting with
![]() $\tau _1$
. Finally, the outcomes of the form
$\tau _1$
. Finally, the outcomes of the form
![]() $\left \ulcorner (\uparrow ,n,m)\right \urcorner $
correspond to the case where we find n elements in
$\left \ulcorner (\uparrow ,n,m)\right \urcorner $
correspond to the case where we find n elements in
![]() $\Theta ^{\xi }$
extending to e-splittings with
$\Theta ^{\xi }$
extending to e-splittings with
![]() $\tau _0$
after which we find another m elements extending to an e-splitting with
$\tau _0$
after which we find another m elements extending to an e-splitting with
![]() $\tau _1$
but infinitely many elements don’t extend to an e-splitting with either.
$\tau _1$
but infinitely many elements don’t extend to an e-splitting with either.
Let
![]() $\nu = \langle \alpha \widehat {\phantom {x}}\langle o\rangle , \sigma \rangle $
for whatever value we specify for the outcome o. We’ll ensure that
$\nu = \langle \alpha \widehat {\phantom {x}}\langle o\rangle , \sigma \rangle $
for whatever value we specify for the outcome o. We’ll ensure that
![]() ${\theta ^{\nu }_{0}}$
e-splits with
${\theta ^{\nu }_{0}}$
e-splits with
![]() ${\theta ^{\nu }_{n+1}}, n \in \omega $
in all cases except when
${\theta ^{\nu }_{n+1}}, n \in \omega $
in all cases except when
![]() $o = \left \ulcorner {\,\not |\,}\right \urcorner $
or
$o = \left \ulcorner {\,\not |\,}\right \urcorner $
or
![]() $o = \left \ulcorner (\uparrow ,n,m)\right \urcorner $
. In the latter case, we’ll ensure that neither
$o = \left \ulcorner (\uparrow ,n,m)\right \urcorner $
. In the latter case, we’ll ensure that neither
![]() $\tau _0$
or
$\tau _0$
or
![]() $\tau _1$
e-split with any extension of
$\tau _1$
e-split with any extension of
![]() ${\theta ^{{\nu }}_{n+1}}, n \in \omega $
(ensuring that if
${\theta ^{{\nu }}_{n+1}}, n \in \omega $
(ensuring that if
![]() $f \succ {\theta ^{\nu }_{n+1}}$
then
$f \succ {\theta ^{\nu }_{n+1}}$
then
![]() $\Phi _{e}\left (f \oplus X\right )\uparrow $
). Since we don’t want to accidentally extend
$\Phi _{e}\left (f \oplus X\right )\uparrow $
). Since we don’t want to accidentally extend
![]() ${\theta ^{{\langle \alpha \widehat {\phantom {x}}\langle o'\rangle , \sigma \rangle }}_{0}}$
to an infinite path if
${\theta ^{{\langle \alpha \widehat {\phantom {x}}\langle o'\rangle , \sigma \rangle }}_{0}}$
to an infinite path if
![]() $o'$
isn’t the true outcome we’ll ensure that every outcome except
$o'$
isn’t the true outcome we’ll ensure that every outcome except
![]() $\left \ulcorner {\,\not |\,}\right \urcorner $
corresponds to an incompatible value for
$\left \ulcorner {\,\not |\,}\right \urcorner $
corresponds to an incompatible value for
![]() ${\theta ^{{\langle \alpha \widehat {\phantom {x}}\langle o'\rangle , \sigma \rangle }}_{0}}$
of length at most
${\theta ^{{\langle \alpha \widehat {\phantom {x}}\langle o'\rangle , \sigma \rangle }}_{0}}$
of length at most
![]() $1 + \max \left \lvert \tau _0\right \rvert , \left \lvert \tau _1\right \rvert $
while always ensuring that
$1 + \max \left \lvert \tau _0\right \rvert , \left \lvert \tau _1\right \rvert $
while always ensuring that
![]() ${\theta ^{{\nu }}_{0}} \succ {\theta ^{\xi }_{0}}$
.
${\theta ^{{\nu }}_{0}} \succ {\theta ^{\xi }_{0}}$
.
We define
![]() $\delta ^{\nu } = \delta ^{\xi }$
for all potential outcomes o. When
$\delta ^{\nu } = \delta ^{\xi }$
for all potential outcomes o. When
![]() $s_\xi = 0$
we start by setting
$s_\xi = 0$
we start by setting
![]() $\tau _0, \tau _1$
to be undefined and
$\tau _0, \tau _1$
to be undefined and
![]() $\hat {n} = \hat {m} = 0$
. For
$\hat {n} = \hat {m} = 0$
. For
![]() $s_\xi> 0$
we consider the following cases.
$s_\xi> 0$
we consider the following cases.
-
Case
 $\tau _0\uparrow :$
Check if there are
$\tau _0\uparrow :$
Check if there are
 $\tau _0, \tau _1 \in T_s$
with
$\tau _0, \tau _1 \in T_s$
with
 $\tau _0, \tau _1$
e-splitting extensions of
$\tau _0, \tau _1$
e-splitting extensions of
 ${\theta ^{\xi }_{0}}$
. If no such values are found, then visit outcome
${\theta ^{\xi }_{0}}$
. If no such values are found, then visit outcome
 $o = \left \ulcorner {\,\not |\,}\right \urcorner $
and define
$o = \left \ulcorner {\,\not |\,}\right \urcorner $
and define
 $\Theta ^{\nu } = \Theta ^{\xi }$
. If such values are found, let
$\Theta ^{\nu } = \Theta ^{\xi }$
. If such values are found, let
 $\tau _0, \tau _1$
be
$\tau _0, \tau _1$
be
 $\prec $
maximal extensions in
$\prec $
maximal extensions in
 $T_s$
of these e-splitting extensions of
$T_s$
of these e-splitting extensions of
 ${\theta ^{\xi }_{0}}$
, let
${\theta ^{\xi }_{0}}$
, let
 $\hat {m} = \hat {n} = n$
and visit outcome
$\hat {m} = \hat {n} = n$
and visit outcome
 $o = \left \ulcorner \mid _0\right \urcorner $
setting
$o = \left \ulcorner \mid _0\right \urcorner $
setting
 ${\theta ^{\nu }_{0}} = \tau _0$
.
${\theta ^{\nu }_{0}} = \tau _0$
. -
Case
 $\tau _0\downarrow : $
We break this up into a number of subcases. We search for some
$\tau _0\downarrow : $
We break this up into a number of subcases. We search for some
 $n \leq s_\xi $
and
$n \leq s_\xi $
and
 $\tau ' \succ {\theta ^{\xi }_{n}}, \tau ' \in T_s$
that satisfy the following (picking the first case satisfied):
$\tau ' \succ {\theta ^{\xi }_{n}}, \tau ' \in T_s$
that satisfy the following (picking the first case satisfied):-
Case
 $\tau ', \tau _0 $
e-split with
$\tau ', \tau _0 $
e-split with
 $\hat {n} < n \leq s_\xi $
: In this case, we let
$\hat {n} < n \leq s_\xi $
: In this case, we let
 $o = \left \ulcorner \mid _0\right \urcorner $
and set
$o = \left \ulcorner \mid _0\right \urcorner $
and set
 ${\theta ^{\nu }_{s_\nu }}$
to be a
${\theta ^{\nu }_{s_\nu }}$
to be a
 $\prec $
maximal extension of
$\prec $
maximal extension of
 $\tau '$
in
$\tau '$
in
 $ T_s$
. Finally, we set
$ T_s$
. Finally, we set
 $\hat {n} = \hat {m} = n$
.
$\hat {n} = \hat {m} = n$
. -
Case
 $\tau ', \tau _1 $
e-split with
$\tau ', \tau _1 $
e-split with
 $\hat {m} < n \leq s_\xi $
: In this case, we let
$\hat {m} < n \leq s_\xi $
: In this case, we let
 $o = \left \ulcorner (\mid _1, \hat {n})\right \urcorner $
and set
$o = \left \ulcorner (\mid _1, \hat {n})\right \urcorner $
and set
 $\hat {m} = n$
and
$\hat {m} = n$
and
 ${\theta ^{\nu }_{s_\nu +1}}$
be a
${\theta ^{\nu }_{s_\nu +1}}$
be a
 $\prec $
maximal extension of
$\prec $
maximal extension of
 $\tau '$
in
$\tau '$
in
 $T_s$
.
$T_s$
.If this is the first time we’ve visited this outcome
 $s_\nu = 0$
. We pick k to be larger than any number mentioned so far in this construction, and set
$s_\nu = 0$
. We pick k to be larger than any number mentioned so far in this construction, and set
 ${\theta ^{\nu }_{0}} =\tau _1\widehat {\phantom {x}}\langle k\rangle $
placing
${\theta ^{\nu }_{0}} =\tau _1\widehat {\phantom {x}}\langle k\rangle $
placing
 $ {\theta ^{\nu }_{0}}$
into
$ {\theta ^{\nu }_{0}}$
into
 $T_{s+1}$
.
$T_{s+1}$
. -
Case Otherwise: In this case, we visit outcome
 $o = \left \ulcorner (\uparrow ,\hat {n},\hat {m})\right \urcorner $
. If this is the first time we’ve visited this outcome, set
$o = \left \ulcorner (\uparrow ,\hat {n},\hat {m})\right \urcorner $
. If this is the first time we’ve visited this outcome, set
 ${\theta ^{\nu }_{0}} =\tau _1\widehat {\phantom {x}}\langle k\rangle $
. Let
${\theta ^{\nu }_{0}} =\tau _1\widehat {\phantom {x}}\langle k\rangle $
. Let
 $\tau '$
be a
$\tau '$
be a
 $ \prec $
maximal element of
$ \prec $
maximal element of
 $T_s$
extending
$T_s$
extending
 ${\theta ^{\xi }_{\hat {m} + s_\nu + 1}}$
and set
${\theta ^{\xi }_{\hat {m} + s_\nu + 1}}$
and set
 ${\theta ^{\nu }_{s_\nu +1}} = \tau '$
.
${\theta ^{\nu }_{s_\nu +1}} = \tau '$
.
-
6.3.7 Module
 ${ \mathcal {H}}_{\sigma }$
.
${ \mathcal {H}}_{\sigma }$
.
We note that we can assume (see Lemma B.7) we have a uniformly given total computable binary valued function (indeed functional)
![]() $\rho (\sigma , s_1, s_0)$
such that
$\rho (\sigma , s_1, s_0)$
such that
![]() $\rho _1(\sigma , s_1) = \lim _{s_0 \to \infty } \rho (\sigma , s_1, s_0)$
is total,
$\rho _1(\sigma , s_1) = \lim _{s_0 \to \infty } \rho (\sigma , s_1, s_0)$
is total,
![]() $S(\sigma ) = \lim _{s_1 \to \infty } \rho _1(\sigma , s_1)$
(both diverging if either does).
$S(\sigma ) = \lim _{s_1 \to \infty } \rho _1(\sigma , s_1)$
(both diverging if either does).
Morally speaking, this module has the outcomes
![]() $\left \ulcorner (i, \hat {n})\right \urcorner $
ordered lexicographically where
$\left \ulcorner (i, \hat {n})\right \urcorner $
ordered lexicographically where
![]() $i \in {\left \{0,1\right \}}$
indicates whether the module guesses that
$i \in {\left \{0,1\right \}}$
indicates whether the module guesses that
![]() $\sigma \notin S$
or
$\sigma \notin S$
or
![]() $\sigma \in S$
and
$\sigma \in S$
and
![]() $\hat {n}$
indicates the value at which
$\hat {n}$
indicates the value at which
![]() $\rho _1$
achieves its limit. However, to ensure that we never reinitialize any node as required by Condition 1 we also record a value m giving the number of times an outcome to the left of
$\rho _1$
achieves its limit. However, to ensure that we never reinitialize any node as required by Condition 1 we also record a value m giving the number of times an outcome to the left of
![]() $(i, \hat {n})$
has been visited. Thus, the actual outcomes will be of the form
$(i, \hat {n})$
has been visited. Thus, the actual outcomes will be of the form
![]() $\left \ulcorner (i, \hat {n}, m)\right \urcorner = 2\langle \hat {n}, m\rangle +i$
. As our pairing function is strictly monotonic in both arguments this functions just as if we’d used outcomes of the form
$\left \ulcorner (i, \hat {n}, m)\right \urcorner = 2\langle \hat {n}, m\rangle +i$
. As our pairing function is strictly monotonic in both arguments this functions just as if we’d used outcomes of the form
![]() $\left \ulcorner (i, \hat {n})\right \urcorner $
and reinitialized outcomes after passing to their left.
$\left \ulcorner (i, \hat {n})\right \urcorner $
and reinitialized outcomes after passing to their left.
![]() $\mathfrak {O}(\xi )$
consists of all pairs
$\mathfrak {O}(\xi )$
consists of all pairs
![]() $(o, \delta )$
where o is one of the allowed outcomes and
$(o, \delta )$
where o is one of the allowed outcomes and
![]() $\delta = \langle \rangle $
.
$\delta = \langle \rangle $
.
If
![]() $s_\xi = 0$
set
$s_\xi = 0$
set
![]() $\tau $
to be a
$\tau $
to be a
![]() $\prec $
maximal extension of
$\prec $
maximal extension of
![]() $\delta ^{\xi }$
in
$\delta ^{\xi }$
in
![]() $T_s$
. If
$T_s$
. If
![]() $s_\xi> 0$
we define k to be the number of times before stage s at which an outcome of the form
$s_\xi> 0$
we define k to be the number of times before stage s at which an outcome of the form
![]() $ \left \ulcorner (i, \hat {n}, m)\right \urcorner $
has been visited. Choose the lexicographically least pair
$ \left \ulcorner (i, \hat {n}, m)\right \urcorner $
has been visited. Choose the lexicographically least pair
![]() $(i, \hat {n})$
such that for all
$(i, \hat {n})$
such that for all
![]() $n \in [\hat {n}, \hat {n} + k]$
there are
$n \in [\hat {n}, \hat {n} + k]$
there are
![]() $k + 1$
distinct values
$k + 1$
distinct values
![]() $x^{n}_j \leq s, j < k +1$
such that
$x^{n}_j \leq s, j < k +1$
such that
![]() $i = \rho (\sigma , n, x^{n}_j)$
. Note that, such a pair is always found since for large enough
$i = \rho (\sigma , n, x^{n}_j)$
. Note that, such a pair is always found since for large enough
![]() $\hat {n}$
we have
$\hat {n}$
we have
![]() $k = 0$
and
$k = 0$
and
![]() $\rho (\sigma , \hat {n}, 0) \in {\left \{0,1\right \}}$
. We now visit the outcome
$\rho (\sigma , \hat {n}, 0) \in {\left \{0,1\right \}}$
. We now visit the outcome
![]() $o = \left \ulcorner (i, \hat {n}, m)\right \urcorner $
where m is the number of times that we’ve visited an outcome of the form
$o = \left \ulcorner (i, \hat {n}, m)\right \urcorner $
where m is the number of times that we’ve visited an outcome of the form
![]() $\left \ulcorner (i', n, m)\right \urcorner $
with
$\left \ulcorner (i', n, m)\right \urcorner $
with
![]() $(i',n)$
lexicographically before
$(i',n)$
lexicographically before
![]() $(i, \hat {n})$
before stage s.
$(i, \hat {n})$
before stage s.
If this is the first time we’ve visited outcome o then pick c to be large, enumerate
![]() $\tau \widehat {\phantom {x}}\langle c\rangle $
into
$\tau \widehat {\phantom {x}}\langle c\rangle $
into
![]() $T_{s+1}$
, and set
$T_{s+1}$
, and set
![]() $\delta ^{\langle \alpha \widehat {\phantom {x}}\langle o\rangle , \sigma \rangle } = \tau \widehat {\phantom {x}}\langle c\rangle $
.
$\delta ^{\langle \alpha \widehat {\phantom {x}}\langle o\rangle , \sigma \rangle } = \tau \widehat {\phantom {x}}\langle c\rangle $
.
6.4 Verification
Before we verify the individual requirements, we verify that the construction controls the paths through T in the manner desired.
Lemma 6.7. Suppose that ![]() implements a module of the form
implements a module of the form
![]() ${\mathcal {P}}_{e}, {\mathcal {L}}_{e}, {\mathcal {L}}^n_{e}, {\mathcal {H}}_{\sigma }$
and that for some
${\mathcal {P}}_{e}, {\mathcal {L}}_{e}, {\mathcal {L}}^n_{e}, {\mathcal {H}}_{\sigma }$
and that for some
![]() $\nu $
with
$\nu $
with
![]() $\nu ^{-} = \xi $
we have
$\nu ^{-} = \xi $
we have
![]() $\lvert \tau \rvert = \left \lvert {\delta ^{\nu }}\right \rvert $
but
$\lvert \tau \rvert = \left \lvert {\delta ^{\nu }}\right \rvert $
but
![]() $\tau \nsucc \delta ^{\hat {\xi }}$
for
$\tau \nsucc \delta ^{\hat {\xi }}$
for ![]() ,
,
![]() $\hat {\xi }^{-} = \xi $
. Then there are only finitely many stages at which any module at
$\hat {\xi }^{-} = \xi $
. Then there are only finitely many stages at which any module at
![]() $\hat {\nu } \succ \xi $
enumerates an element
$\hat {\nu } \succ \xi $
enumerates an element
![]() $\tau ' \succ \tau $
into T.
$\tau ' \succ \tau $
into T.
Note that this covers the case where
![]() ${\mathcal {H}}_{\sigma }$
doesn’t have any extension
${\mathcal {H}}_{\sigma }$
doesn’t have any extension
![]() $\nu $
in the truepath because S doesn’t converge on
$\nu $
in the truepath because S doesn’t converge on
![]() $\sigma $
.
$\sigma $
.
Proof By Condition 3 and Condition 2 (and the fact that no single module ever adds a full path) it is enough to show that there are only finitely many stages at which we visit a node
![]() $ \hat {\nu }$
with
$ \hat {\nu }$
with
![]() $\hat {\nu } \succneqq \xi $
and
$\hat {\nu } \succneqq \xi $
and
![]() $\delta ^{\hat {\nu }}$
compatible with
$\delta ^{\hat {\nu }}$
compatible with
![]() $\tau $
.
$\tau $
.
For the module
![]() ${\mathcal {L}}^n_{e}$
this is trivial as this module only has a single outcome. For the module
${\mathcal {L}}^n_{e}$
this is trivial as this module only has a single outcome. For the module
![]() ${\mathcal {H}}_{\sigma }$
we note that each time visit to an outcome
${\mathcal {H}}_{\sigma }$
we note that each time visit to an outcome
![]() $\left \ulcorner i, \hat {n}, m\right \urcorner $
ensures that all outcomes to the right visit strings that have never been visited before. As
$\left \ulcorner i, \hat {n}, m\right \urcorner $
ensures that all outcomes to the right visit strings that have never been visited before. As
![]() ${\mathcal {P}}_{e}$
can act at most once this case is also straightforward.
${\mathcal {P}}_{e}$
can act at most once this case is also straightforward.
This leaves only the case
![]() ${\mathcal {L}}_{e}$
. If this module takes any of the finite outcomes the claim is evident and if this module takes the outcome
${\mathcal {L}}_{e}$
. If this module takes any of the finite outcomes the claim is evident and if this module takes the outcome
![]() $\left \ulcorner \downarrow \right \urcorner $
then the claim follows because
$\left \ulcorner \downarrow \right \urcorner $
then the claim follows because
![]() $\delta ^{\nu } \succ \delta ^{\hat {\xi }}$
for all
$\delta ^{\nu } \succ \delta ^{\hat {\xi }}$
for all
![]() $\nu $
with
$\nu $
with
![]() $\nu ^{-} = \xi $
when
$\nu ^{-} = \xi $
when
![]() $\hat {\xi }$
corresponds to the infinitary outcome.
$\hat {\xi }$
corresponds to the infinitary outcome.
Lemma 6.8. Suppose that ![]() and
and
![]() $\xi ^{-}$
implements a module of the form
$\xi ^{-}$
implements a module of the form
![]() ${\mathcal {H}}^+_{\sigma }$
or
${\mathcal {H}}^+_{\sigma }$
or
![]() ${\mathcal {S}}^n_{e}, e \geq 0$
then for each k there is some l such that if
${\mathcal {S}}^n_{e}, e \geq 0$
then for each k there is some l such that if
![]() $\tau \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle , \lvert \tau \rvert \geq l$
but
$\tau \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle , \lvert \tau \rvert \geq l$
but
![]() $\tau \nsucc {\theta ^{\xi }_{n}}$
for any n then there are only finitely many stages at which some
$\tau \nsucc {\theta ^{\xi }_{n}}$
for any n then there are only finitely many stages at which some
![]() $\nu \succ \xi ^{-}$
enumerates an extension of
$\nu \succ \xi ^{-}$
enumerates an extension of
![]() $\tau $
.
$\tau $
.
Proof This is trivial if
![]() $\xi ^{-}$
implements a module of the form
$\xi ^{-}$
implements a module of the form
![]() ${\mathcal {H}}^+_{\sigma }$
. Also, if there is no
${\mathcal {H}}^+_{\sigma }$
. Also, if there is no
![]() ${\theta ^{\xi }_{n}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
then there is some last stage at which we visit any
${\theta ^{\xi }_{n}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
then there is some last stage at which we visit any
![]() $\nu $
with
$\nu $
with
![]() $\nu ^{-} = \xi ^{-}$
with
$\nu ^{-} = \xi ^{-}$
with
![]() $\Theta ^{\nu }$
containing an extension of
$\Theta ^{\nu }$
containing an extension of
![]() $\delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
. So suppose that
$\delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
. So suppose that
![]() ${\theta ^{\xi }_{n}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
. If
${\theta ^{\xi }_{n}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
. If
![]() $n> 0$
then, once we set
$n> 0$
then, once we set
![]() ${\theta ^{\xi }_{n}}$
we never visit any
${\theta ^{\xi }_{n}}$
we never visit any
![]() $\nu \neq \xi $
with
$\nu \neq \xi $
with
![]() $\nu ^{-} = \xi ^{-}$
with
$\nu ^{-} = \xi ^{-}$
with
![]() ${\theta ^{\xi }_{m}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
.
${\theta ^{\xi }_{m}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
.
This leaves only the case where
![]() ${\theta ^{\xi }_{0}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
. If
${\theta ^{\xi }_{0}} \succ \delta ^{\xi }\widehat {\phantom {x}}\langle k\rangle $
. If
![]() $\xi $
corresponds to an outcome
$\xi $
corresponds to an outcome
![]() $\left \ulcorner (\uparrow ,n,m)\right \urcorner $
or
$\left \ulcorner (\uparrow ,n,m)\right \urcorner $
or
![]() $\left \ulcorner {\,\not |\,}\right \urcorner $
then we never again visit another extension of
$\left \ulcorner {\,\not |\,}\right \urcorner $
then we never again visit another extension of
![]() $ \xi ^{-}$
after visiting
$ \xi ^{-}$
after visiting
![]() $\xi $
so the bound can be deduced by looking at the finitely many stages before that happens. Thus, we can assume
$\xi $
so the bound can be deduced by looking at the finitely many stages before that happens. Thus, we can assume
![]() $\xi $
corresponds either to
$\xi $
corresponds either to
![]() $\left \ulcorner \mid _0\right \urcorner $
or
$\left \ulcorner \mid _0\right \urcorner $
or
![]() $ \left \ulcorner (\mid _1, n)\right \urcorner $
. In this case, we can take
$ \left \ulcorner (\mid _1, n)\right \urcorner $
. In this case, we can take
![]() $l = 1 + \max \left \lvert \tau _0\right \rvert , \left \lvert \tau _1\right \rvert $
by the remark in Section 6.3.6.
$l = 1 + \max \left \lvert \tau _0\right \rvert , \left \lvert \tau _1\right \rvert $
by the remark in Section 6.3.6.
Lemma 6.9. For all
![]() $f \in \omega ^{\omega }$
,
$f \in \omega ^{\omega }$
,
![]() $f \in [T]$
iff
$f \in [T]$
iff
![]() $\left (\exists g \in \omega ^{\omega }\right )\!\left (\hat {T}(g) = f \right )$
.
$\left (\exists g \in \omega ^{\omega }\right )\!\left (\hat {T}(g) = f \right )$
.
Proof For the if direction suppose that
![]() $\hat {T}(g) = f$
. Since any module
$\hat {T}(g) = f$
. Since any module
![]() ${\mathcal {M}}_{\xi ^{-}}$
which sets
${\mathcal {M}}_{\xi ^{-}}$
which sets
![]() $\delta ^{\xi } = \sigma $
guarantees that
$\delta ^{\xi } = \sigma $
guarantees that
![]() $\sigma \in T$
(and we always have
$\sigma \in T$
(and we always have
![]() $\sigma ^{-} \in T$
) and we have that
$\sigma ^{-} \in T$
) and we have that
![]() $ \hat {T}(g) \in T$
. For the other direction, suppose
$ \hat {T}(g) \in T$
. For the other direction, suppose
![]() $f \neq \hat {T}(g)$
for any g. Let
$f \neq \hat {T}(g)$
for any g. Let
![]() $\xi $
be a
$\xi $
be a
![]() $\prec $
minimal element such that
$\prec $
minimal element such that
![]() $\delta ^{\xi ^{-}} \prec f$
and, if
$\delta ^{\xi ^{-}} \prec f$
and, if
![]() $\Theta ^{\xi ^{-}}$
defined, with f extending some element in
$\Theta ^{\xi ^{-}}$
defined, with f extending some element in
![]() $\Theta ^{\xi ^{-}}$
but one of those conditions failing for
$\Theta ^{\xi ^{-}}$
but one of those conditions failing for
![]() $\xi $
. We then argue using Lemmas 6.7 and 6.8 that there is some
$\xi $
. We then argue using Lemmas 6.7 and 6.8 that there is some
![]() $\tau \prec f$
such that only finitely many extensions of
$\tau \prec f$
such that only finitely many extensions of
![]() $\tau $
are enumerated into T.
$\tau $
are enumerated into T.
The only other real difficulty occurs with nodes of the form
![]() ${\mathcal {L}}_{e}$
since those are the only modules that might be assigned to some
${\mathcal {L}}_{e}$
since those are the only modules that might be assigned to some ![]() where the above lemmas (or, for
where the above lemmas (or, for
![]() ${\mathcal {L}}_{e}$
, fact that we only visit incorrect outcomes finitely many times) don’t directly exclude the possibility that some module extending an outcome to the right of the true outcome of
${\mathcal {L}}_{e}$
, fact that we only visit incorrect outcomes finitely many times) don’t directly exclude the possibility that some module extending an outcome to the right of the true outcome of
![]() $\nu $
could contribute infinitely many elements compatible with f. Unless the outcome of
$\nu $
could contribute infinitely many elements compatible with f. Unless the outcome of
![]() $\nu $
is
$\nu $
is
![]() $\left \ulcorner \downarrow \right \urcorner $
this clearly can’t happen as in those cases we settle on the true outcome after finitely many stages. However, there will only be finitely many stages at which
$\left \ulcorner \downarrow \right \urcorner $
this clearly can’t happen as in those cases we settle on the true outcome after finitely many stages. However, there will only be finitely many stages at which
![]() $\nu $
visits an outcome of the form
$\nu $
visits an outcome of the form
![]() $\left \ulcorner \eta \right \urcorner $
where
$\left \ulcorner \eta \right \urcorner $
where
![]() $\delta ^{\eta } \prec f$
ensuring that the false outcomes of
$\delta ^{\eta } \prec f$
ensuring that the false outcomes of
![]() $\nu $
don’t cause a problem.
$\nu $
don’t cause a problem.
Note that, all modules excepting those of the form
![]() ${\mathcal {H}}_{\sigma }$
clearly have a well-defined leftmost outcome that’s visited infinitely often and by Lemma 6.7, in the case where
${\mathcal {H}}_{\sigma }$
clearly have a well-defined leftmost outcome that’s visited infinitely often and by Lemma 6.7, in the case where
![]() $\xi $
implements
$\xi $
implements
![]() ${\mathcal {H}}_{\sigma }$
and
${\mathcal {H}}_{\sigma }$
and
![]() $\xi $
has no successor along the truepath is also a case where
$\xi $
has no successor along the truepath is also a case where
![]() $\delta ^{\xi }$
can’t be extended to any path through T.
$\delta ^{\xi }$
can’t be extended to any path through T.
With this result in hand, we can now verify the properties claimed in Proposition 4.1.
Lemma 6.10.
![]() $\mathrm {rng} \hat {T} \subset T$
and
$\mathrm {rng} \hat {T} \subset T$
and
![]() $[\hat {T}] = [T]$
, that is, claim 1 of Proposition 4.1 holds.
$[\hat {T}] = [T]$
, that is, claim 1 of Proposition 4.1 holds.
Proof By Condition 2 anytime a module sets
![]() $\delta ^{\xi } = \tau $
; it ensures that
$\delta ^{\xi } = \tau $
; it ensures that
![]() $\tau \in T$
. This ensures the first part of the claim holds. The second half of the claim is just Lemma 6.9.
$\tau \in T$
. This ensures the first part of the claim holds. The second half of the claim is just Lemma 6.9.
Lemma 6.11. If ![]() and
and
![]() $\xi $
implements
$\xi $
implements
![]() ${\mathcal {H}}_{\sigma }$
then
${\mathcal {H}}_{\sigma }$
then
![]() $\xi $
has a well-defined outcome iff
$\xi $
has a well-defined outcome iff
![]() $S(\sigma )\downarrow $
and that outcome is always correct about the membership of
$S(\sigma )\downarrow $
and that outcome is always correct about the membership of
![]() $\sigma $
in S.
$\sigma $
in S.
By well-defined outcome we mean a leftmost outcome that is visited infinitely often.
Proof Suppose that the module at
![]() $\xi $
has the true outcome
$\xi $
has the true outcome
![]() $\left \ulcorner (i, \hat {n}, m)\right \urcorner $
. If
$\left \ulcorner (i, \hat {n}, m)\right \urcorner $
. If
![]() $S(\sigma ) \neq i$
(including divergence) then, since
$S(\sigma ) \neq i$
(including divergence) then, since
![]() $\rho _1(\sigma , s_1)$
(first limit), can be taken to be always defined, then for some
$\rho _1(\sigma , s_1)$
(first limit), can be taken to be always defined, then for some
![]() $n> \hat {n}$
we have
$n> \hat {n}$
we have
![]() $\rho _1(\sigma , n) = 1 -i$
. Thus, for some k we have
$\rho _1(\sigma , n) = 1 -i$
. Thus, for some k we have
![]() $\rho (\sigma , n, k') = 1 - i$
for all
$\rho (\sigma , n, k') = 1 - i$
for all
![]() $k' \geq k$
contradicting the assumption that we visit this outcome more than
$k' \geq k$
contradicting the assumption that we visit this outcome more than
![]() $ n + k + 1$
times. Thus,
$ n + k + 1$
times. Thus,
![]() ${\mathcal {H}}_{\sigma }$
is never incorrect and thus must not have an outcome whenever
${\mathcal {H}}_{\sigma }$
is never incorrect and thus must not have an outcome whenever
![]() $S(\sigma )\uparrow $
.
$S(\sigma )\uparrow $
.
Now suppose that
![]() $S(\sigma )\downarrow = i$
. For some minimal
$S(\sigma )\downarrow = i$
. For some minimal
![]() $\hat {n}$
we have
$\hat {n}$
we have
![]() $\rho _1(\sigma , s_1) = i$
for all
$\rho _1(\sigma , s_1) = i$
for all
![]() $s_1 \geq \hat {n}$
. By minimality, there is some last stage at which any outcome of the form
$s_1 \geq \hat {n}$
. By minimality, there is some last stage at which any outcome of the form
![]() $\left \ulcorner (i, n, m)\right \urcorner $
with
$\left \ulcorner (i, n, m)\right \urcorner $
with
![]() $n < \hat {n}$
is visited and as
$n < \hat {n}$
is visited and as
![]() $\rho _1(\sigma , \hat {n}) = i$
there is some last stage at which any outcome of the form
$\rho _1(\sigma , \hat {n}) = i$
there is some last stage at which any outcome of the form
![]() $\left \ulcorner (1 - i, \hat {n}, m)\right \urcorner $
is visited. Thus, after some point we never visit an outcome of the form
$\left \ulcorner (1 - i, \hat {n}, m)\right \urcorner $
is visited. Thus, after some point we never visit an outcome of the form
![]() $\left \ulcorner (i', n, m)\right \urcorner $
with
$\left \ulcorner (i', n, m)\right \urcorner $
with
![]() $(i', n)$
lexicographically before
$(i', n)$
lexicographically before
![]() $(i, \hat {n})$
and thus there is some m for which
$(i, \hat {n})$
and thus there is some m for which
![]() $\left \ulcorner (i, \hat {n}, m)\right \urcorner $
is the true outcome.
$\left \ulcorner (i, \hat {n}, m)\right \urcorner $
is the true outcome.
Lemma 6.12. For all
![]() $g \in \omega ^{\omega }$
,
$g \in \omega ^{\omega }$
,
![]() $\hat {T}(g)$
is total iff
$\hat {T}(g)$
is total iff
![]() $g \in [S]$
iff
$g \in [S]$
iff
![]() $\hat {T}(g) \in [T]$
. Moreover,
$\hat {T}(g) \in [T]$
. Moreover,
![]() $\hat {T}(\sigma )\downarrow $
iff
$\hat {T}(\sigma )\downarrow $
iff
![]() $S(\sigma )\downarrow $
and all
$S(\sigma )\downarrow $
and all ![]() are in S.
are in S.
Proof We first verify the moreover claim. Note that, for any module besides
![]() ${\mathcal {H}}_{\sigma }$
there is always a well-defined true outcome. Thus, by an examination of the construction, we can see that the only way for
${\mathcal {H}}_{\sigma }$
there is always a well-defined true outcome. Thus, by an examination of the construction, we can see that the only way for
![]() $ \hat {T}(\sigma )$
to be undefined is either if for some
$ \hat {T}(\sigma )$
to be undefined is either if for some ![]() the module of the form
the module of the form
![]() ${\mathcal {H}}_{\sigma '}$
on the truepath doesn’t have a true outcome guessing
${\mathcal {H}}_{\sigma '}$
on the truepath doesn’t have a true outcome guessing
![]() $\sigma ' \in S$
or if the module
$\sigma ' \in S$
or if the module
![]() $ {\mathcal {H}}_{\sigma }$
on the truepath doesn’t have any true outcome. Clearly, if either of those cases obtain then we actually do have
$ {\mathcal {H}}_{\sigma }$
on the truepath doesn’t have any true outcome. Clearly, if either of those cases obtain then we actually do have
![]() $\hat {T}(\sigma )\uparrow $
, so this result follows from Lemma 6.11.
$\hat {T}(\sigma )\uparrow $
, so this result follows from Lemma 6.11.
The main claim follows trivially since
![]() $g \in [S]$
iff all
$g \in [S]$
iff all
![]() $\sigma \prec g$
are elements in S.
$\sigma \prec g$
are elements in S.
Lemma 6.13.
![]() $\hat {T}$
is an f-tree.
$\hat {T}$
is an f-tree.
Proof As
![]() $\hat {T}$
is clearly
$\hat {T}$
is clearly
![]() $\prec $
respecting it is enough to show that whenever
$\prec $
respecting it is enough to show that whenever
![]() $\hat {T}(\sigma )$
isn’t terminal then
$\hat {T}(\sigma )$
isn’t terminal then
![]() $i < j$
implies that
$i < j$
implies that
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
and
$\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
and
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle j\rangle )$
extend incompatible immediate extensions of
$\hat {T}(\sigma \widehat {\phantom {x}}\langle j\rangle )$
extend incompatible immediate extensions of
![]() $\hat {T}(\sigma )$
and
$\hat {T}(\sigma )$
and
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
is lexicographically below
$\hat {T}(\sigma \widehat {\phantom {x}}\langle i\rangle )$
is lexicographically below
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle j\rangle )$
. However, this is immediate from the operation of
$\hat {T}(\sigma \widehat {\phantom {x}}\langle j\rangle )$
. However, this is immediate from the operation of
![]() ${\mathcal {H}}^+_{\sigma }$
and the fact that nodes of the form
${\mathcal {H}}^+_{\sigma }$
and the fact that nodes of the form
![]() ${\mathcal {S}}^n_{e}$
maintain these properties.
${\mathcal {S}}^n_{e}$
maintain these properties.
We can use this to prove the homeomorphism claim from Proposition 4.1.
Lemma 6.14.
![]() $\hat {T}$
is a homeomorphism of
$\hat {T}$
is a homeomorphism of
![]() $[S]$
with
$[S]$
with
![]() $[T]$
. That is claim 2 of Proposition 4.1 holds.
$[T]$
. That is claim 2 of Proposition 4.1 holds.
Proof By Lemma 6.12 we know that
![]() $[T]$
is the image of
$[T]$
is the image of
![]() $[S]$
under
$[S]$
under
![]() $\hat {T}$
. Evidently, both
$\hat {T}$
. Evidently, both
![]() $\hat {T}$
and its inverse are continuous, so it remains only to show that
$\hat {T}$
and its inverse are continuous, so it remains only to show that
![]() $\hat {T}$
is injective. However, this follows from Lemma 6.13.
$\hat {T}$
is injective. However, this follows from Lemma 6.13.
Lemma 6.15. If
![]() $\Upsilon _2$
is a computable functional then we can uniformly find computable functionals
$\Upsilon _2$
is a computable functional then we can uniformly find computable functionals
![]() $\Upsilon , \hat {\Upsilon }$
such that if
$\Upsilon , \hat {\Upsilon }$
such that if
![]() $\Upsilon _2({X}^{\prime \prime }) = S$
then
$\Upsilon _2({X}^{\prime \prime }) = S$
then
![]() $\Upsilon (X) = T$
and
$\Upsilon (X) = T$
and
![]() $\hat {\Upsilon }({X}^{\prime \prime }) = \hat {T}$
where
$\hat {\Upsilon }({X}^{\prime \prime }) = \hat {T}$
where
![]() $T, \hat {T}$
are as constructed above.
$T, \hat {T}$
are as constructed above.
Proof To compute
![]() $\hat {T}(\sigma )$
from
$\hat {T}(\sigma )$
from
![]() ${X}^{\prime \prime }$
we simply (iteratively) identify the leftmost outcome of nodes on
${X}^{\prime \prime }$
we simply (iteratively) identify the leftmost outcome of nodes on
![]() $\mathbb {T}$
to identify elements in
$\mathbb {T}$
to identify elements in ![]() and search for a node
and search for a node ![]() and
and
![]() $\xi ^{-}$
implementing
$\xi ^{-}$
implementing
![]() ${\mathcal {H}}_{\sigma }$
and return
${\mathcal {H}}_{\sigma }$
and return
![]() $\delta ^{\xi }$
. It’s possible that when working to compute
$\delta ^{\xi }$
. It’s possible that when working to compute
![]() $\hat {T}(\sigma )$
we next discover such a node
$\hat {T}(\sigma )$
we next discover such a node
![]() $\xi $
. However, this can only happen when S fails to converge on some
$\xi $
. However, this can only happen when S fails to converge on some
![]() $\sigma ' \prec \sigma $
in which case
$\sigma ' \prec \sigma $
in which case
![]() $\hat {T}(\sigma )$
is properly undefined anyway. The uniformity can be read off the construction (note the only use of S is via Lemma B.7 which is fully uniform).
$\hat {T}(\sigma )$
is properly undefined anyway. The uniformity can be read off the construction (note the only use of S is via Lemma B.7 which is fully uniform).
Lemma 6.16. If
![]() $f \in [T]$
then
$f \in [T]$
then
![]() $f \nleq _{\mathbf {T}} X$
. That is claim 3 of Proposition 4.1 holds.
$f \nleq _{\mathbf {T}} X$
. That is claim 3 of Proposition 4.1 holds.
Proof Suppose the claim fails and for some
![]() $f \in [T], f = \Phi _{e}\left (X\right )$
for some total
$f \in [T], f = \Phi _{e}\left (X\right )$
for some total
![]() $\Phi _{e}\left (X \right )$
. By Lemma 6.9 we have
$\Phi _{e}\left (X \right )$
. By Lemma 6.9 we have
![]() $f = \hat {T}(g)$
. Thus, for some
$f = \hat {T}(g)$
. Thus, for some ![]() with
with
![]() $\xi ^{-}$
implementing
$\xi ^{-}$
implementing
![]() ${\mathcal {P}}_{e}$
we have
${\mathcal {P}}_{e}$
we have
![]() $f \succ \delta ^{\xi }$
. As
$f \succ \delta ^{\xi }$
. As
![]() $f = \hat {T}(g)$
we know that
$f = \hat {T}(g)$
we know that ![]() extends to a node implementing some
extends to a node implementing some
![]() ${\mathcal {H}}^+_{\sigma }$
and thus T contains incompatible
${\mathcal {H}}^+_{\sigma }$
and thus T contains incompatible
![]() $\tau _0, \tau _1 \succ \delta ^{\xi ^{-}}$
. Thus, by the operation of
$\tau _0, \tau _1 \succ \delta ^{\xi ^{-}}$
. Thus, by the operation of
![]() ${\mathcal {P}}_{e}$
we know that
${\mathcal {P}}_{e}$
we know that
![]() $\delta ^{\xi } \mid \Phi _{e}\left (X\right )$
contradicting the supposition.
$\delta ^{\xi } \mid \Phi _{e}\left (X\right )$
contradicting the supposition.
Lemma 6.17. Suppose ![]() and
and
![]() $\xi ^{-}$
implements
$\xi ^{-}$
implements
![]() ${\mathcal {L}}_{e}$
then
${\mathcal {L}}_{e}$
then
![]() $\Phi _{e}\left (f \oplus X\right )$
is total iff the true outcome of
$\Phi _{e}\left (f \oplus X\right )$
is total iff the true outcome of
![]() $\xi ^{-}$
is
$\xi ^{-}$
is
![]() $\left \ulcorner \downarrow \right \urcorner $
.
$\left \ulcorner \downarrow \right \urcorner $
.
Proof Suppose
![]() $\xi ^{-}$
has true outcome
$\xi ^{-}$
has true outcome
![]() $\left \ulcorner \downarrow \right \urcorner $
but that
$\left \ulcorner \downarrow \right \urcorner $
but that
![]() $\Phi _{e}\left (f \oplus X;n\right )\uparrow $
. For some
$\Phi _{e}\left (f \oplus X;n\right )\uparrow $
. For some ![]() with
with
![]() $\nu ^{-} \succ \xi $
implementing
$\nu ^{-} \succ \xi $
implementing
![]() ${\mathcal {L}}^n_{e}$
we have
${\mathcal {L}}^n_{e}$
we have
![]() $f \succ \tau $
and by operation of
$f \succ \tau $
and by operation of
![]() ${\mathcal {L}}_{e}$
and
${\mathcal {L}}_{e}$
and
![]() ${\mathcal {L}}^n_{e}$
we can only have true outcome
${\mathcal {L}}^n_{e}$
we can only have true outcome
![]() $\left \ulcorner \downarrow \right \urcorner $
if
$\left \ulcorner \downarrow \right \urcorner $
if
![]() $\Phi _{e}\left (\tau \oplus X;n\right )\downarrow $
. This contradicts our assumption.
$\Phi _{e}\left (\tau \oplus X;n\right )\downarrow $
. This contradicts our assumption.
On the other hand, if
![]() $\xi ^{-}$
has true outcome
$\xi ^{-}$
has true outcome
![]() $\left \ulcorner \nu \right \urcorner $
then
$\left \ulcorner \nu \right \urcorner $
then
![]() $\nu \succ \xi ^{-}$
implements some
$\nu \succ \xi ^{-}$
implements some
![]() ${\mathcal {L}}^n_{e}$
. The operation of
${\mathcal {L}}^n_{e}$
. The operation of
![]() ${\mathcal {L}}_{e}$
guarantees that if we ever saw some
${\mathcal {L}}_{e}$
guarantees that if we ever saw some
![]() $\tau \succ \delta ^{\xi }, \tau \in T$
with
$\tau \succ \delta ^{\xi }, \tau \in T$
with
![]() $\Phi _{e}\left (\tau \oplus X;n\right )\downarrow $
then we wouldn’t have true outcome
$\Phi _{e}\left (\tau \oplus X;n\right )\downarrow $
then we wouldn’t have true outcome
![]() $\left \ulcorner \nu \right \urcorner $
. Hence, we must have
$\left \ulcorner \nu \right \urcorner $
. Hence, we must have
![]() $\Phi _{e}\left (f \oplus X;n\right )\uparrow $
. As the operation of
$\Phi _{e}\left (f \oplus X;n\right )\uparrow $
. As the operation of
![]() ${\mathcal {L}}_{e}$
ensures that one of our outcomes is true, this establishes the claim.
${\mathcal {L}}_{e}$
ensures that one of our outcomes is true, this establishes the claim.
Lemma 6.18. If
![]() $g \in [S]$
then
$g \in [S]$
then
![]() $g \oplus {X}^{\prime \prime } \equiv _{\mathbf {T}} {\left (\hat {T}(g) \oplus X\right )}^{\prime \prime } \equiv _{\mathbf {T}} \hat {T}(g) \oplus {X}^{\prime \prime }$
. That is claim 4 of Proposition 4.1 holds.
$g \oplus {X}^{\prime \prime } \equiv _{\mathbf {T}} {\left (\hat {T}(g) \oplus X\right )}^{\prime \prime } \equiv _{\mathbf {T}} \hat {T}(g) \oplus {X}^{\prime \prime }$
. That is claim 4 of Proposition 4.1 holds.
Note that, as
![]() $[T]$
is the image of
$[T]$
is the image of
![]() $[S]$
under
$[S]$
under
![]() $\hat {T}$
every
$\hat {T}$
every
![]() $f \in [T]$
has this property relative to some g.
$f \in [T]$
has this property relative to some g.
Proof Let
![]() $g \in [S]$
. By Lemma 6.14,
$g \in [S]$
. By Lemma 6.14,
![]() $\hat {T}(g) = f$
for some total f. Since whenever
$\hat {T}(g) = f$
for some total f. Since whenever
![]() $\hat {T}(\sigma )\downarrow $
by Lemma 6.15 we can find
$\hat {T}(\sigma )\downarrow $
by Lemma 6.15 we can find
![]() $\hat {T}(\sigma )$
computably in
$\hat {T}(\sigma )$
computably in
![]() ${X}^{\prime \prime }$
it follows that
${X}^{\prime \prime }$
it follows that
![]() $f \leq _{\mathbf {T}} g \oplus {X}^{\prime \prime }$
. To see that
$f \leq _{\mathbf {T}} g \oplus {X}^{\prime \prime }$
. To see that
![]() $g \leq _{\mathbf {T}} f \oplus {X}^{\prime \prime }$
note that, by Lemmas 6.15 and 6.13 we can inductively recover the unique path g with
$g \leq _{\mathbf {T}} f \oplus {X}^{\prime \prime }$
note that, by Lemmas 6.15 and 6.13 we can inductively recover the unique path g with
![]() $\hat {T}(g) = f$
computably in
$\hat {T}(g) = f$
computably in
![]() $f \oplus {X}^{\prime \prime }$
.
$f \oplus {X}^{\prime \prime }$
.
Clearly
![]() ${\left (f \oplus X\right )}^{\prime \prime } \geq _{\mathbf {T}} f \oplus {X}^{\prime \prime }$
. Thus, to complete the proof, it is sufficient to show that
${\left (f \oplus X\right )}^{\prime \prime } \geq _{\mathbf {T}} f \oplus {X}^{\prime \prime }$
. Thus, to complete the proof, it is sufficient to show that
![]() ${\left (f \oplus X\right )}^{\prime \prime } \leq _{\mathbf {T}} g \oplus {X}^{\prime \prime }$
. By a well-known result, it is enough to show that
${\left (f \oplus X\right )}^{\prime \prime } \leq _{\mathbf {T}} g \oplus {X}^{\prime \prime }$
. By a well-known result, it is enough to show that
![]() $g \oplus {X}^{\prime \prime }$
can computably decide whether e is an index for a total computable function in
$g \oplus {X}^{\prime \prime }$
can computably decide whether e is an index for a total computable function in
![]() $f \oplus X$
. However, by Lemma 6.17 we can decide this question by searching for
$f \oplus X$
. However, by Lemma 6.17 we can decide this question by searching for ![]() with
with
![]() $\xi $
implementing
$\xi $
implementing
![]() ${\mathcal {L}}_{e}$
and
${\mathcal {L}}_{e}$
and
![]() $\xi = \langle \alpha ,\sigma \rangle $
with
$\xi = \langle \alpha ,\sigma \rangle $
with
![]() $\sigma \prec g$
and determining the outcome of
$\sigma \prec g$
and determining the outcome of
![]() $\xi $
. By Lemma 6.15 this can be done computably in
$\xi $
. By Lemma 6.15 this can be done computably in
![]() $g \oplus {X}^{\prime \prime }$
.
$g \oplus {X}^{\prime \prime }$
.
Lemma 6.19. If
![]() $f \in [T], Y = \Phi _{e}\left (f \oplus X\right )$
and there is some
$f \in [T], Y = \Phi _{e}\left (f \oplus X\right )$
and there is some
![]() $\tau \prec f$
with no e-splitting
$\tau \prec f$
with no e-splitting
![]() $\tau _0, \tau _1 \succ \tau $
with
$\tau _0, \tau _1 \succ \tau $
with
![]() $\tau _0, \tau _1 \in T$
then
$\tau _0, \tau _1 \in T$
then
![]() $Y \leq _{\mathbf {T}} X$
.
$Y \leq _{\mathbf {T}} X$
.
As remarked above, we mean e-splitting relativized to X.
Proof We can compute
![]() $Y{{\restriction _{n}}}$
from X by returning
$Y{{\restriction _{n}}}$
from X by returning
![]() $\Phi _{e}\left (\tau ' \oplus X\right ){{\restriction _{n}}}$
for the first
$\Phi _{e}\left (\tau ' \oplus X\right ){{\restriction _{n}}}$
for the first
![]() $\tau ' \succ \tau $
in T we can find for which this is a string of length n. As
$\tau ' \succ \tau $
in T we can find for which this is a string of length n. As
![]() $Y = \Phi _{e}\left (f \oplus X\right )$
and
$Y = \Phi _{e}\left (f \oplus X\right )$
and
![]() $f \succ \tau , f \in [T]$
there must be some such
$f \succ \tau , f \in [T]$
there must be some such
![]() $\tau '$
and by the lack of e-splitting extensions there is no possibility of an incompatible value.
$\tau '$
and by the lack of e-splitting extensions there is no possibility of an incompatible value.
Lemma 6.20. If
![]() $f \in [T]$
and
$f \in [T]$
and
![]() $Y \leq _{\mathbf {T}} f \oplus X$
then either
$Y \leq _{\mathbf {T}} f \oplus X$
then either
![]() $Y \leq _{\mathbf {T}} X$
or
$Y \leq _{\mathbf {T}} X$
or
![]() $f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
. That is claim 5 of Proposition 4.1 holds.
$f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
. That is claim 5 of Proposition 4.1 holds.
Proof Suppose that
![]() $Y = \Phi _{e}\left (f \oplus X\right )$
and, by Lemma 6.14, that
$Y = \Phi _{e}\left (f \oplus X\right )$
and, by Lemma 6.14, that
![]() $f = \hat {T}(g)$
. Let
$f = \hat {T}(g)$
. Let
![]() $r(\sigma , n)$
where
$r(\sigma , n)$
where
![]() $\lvert \sigma \rvert> e$
be the outcome of the module
$\lvert \sigma \rvert> e$
be the outcome of the module
![]() ${\mathcal {S}}^n_{e}$
assigned to some
${\mathcal {S}}^n_{e}$
assigned to some ![]() and
and ![]() where
where
![]() $\xi ^{-} = (\alpha , \sigma )$
. Note that, for all
$\xi ^{-} = (\alpha , \sigma )$
. Note that, for all
![]() $n, \sigma \in \mathrm {dom} \hat {T}$
with
$n, \sigma \in \mathrm {dom} \hat {T}$
with
![]() $\lvert \sigma \rvert> e$
,
$\lvert \sigma \rvert> e$
,
![]() $\hat {T}(\sigma \widehat {\phantom {x}}\langle n\rangle ) \succ {\theta ^{m(\sigma , n)}_{0}}$
. This is because all modules of the form
$\hat {T}(\sigma \widehat {\phantom {x}}\langle n\rangle ) \succ {\theta ^{m(\sigma , n)}_{0}}$
. This is because all modules of the form
![]() ${\mathcal {S}}^n_{e}, e \geq 0$
always output a leftmost branch extending the leftmost branch they receive as input.
${\mathcal {S}}^n_{e}, e \geq 0$
always output a leftmost branch extending the leftmost branch they receive as input.
If there is some
![]() $\tau \prec f$
not extended by any e-splitting extensions then by Lemma 6.19 we are done. So we may suppose this isn’t the case and show that this implies
$\tau \prec f$
not extended by any e-splitting extensions then by Lemma 6.19 we are done. So we may suppose this isn’t the case and show that this implies
![]() $g \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
which, by Lemma 6.18 is equivalent to showing
$g \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
which, by Lemma 6.18 is equivalent to showing
![]() $f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
.
$f \leq _{\mathbf {T}} Y \oplus {X}^{\prime \prime }$
.
Suppose we know
![]() $\sigma , n'$
and that
$\sigma , n'$
and that
![]() $\sigma \widehat {\phantom {x}}\langle n\rangle \prec g$
for some
$\sigma \widehat {\phantom {x}}\langle n\rangle \prec g$
for some
![]() $n \geq n'$
(where
$n \geq n'$
(where
![]() $\lvert \sigma \rvert> e$
) we demonstrate how to check if
$\lvert \sigma \rvert> e$
) we demonstrate how to check if
![]() $n = n'$
or
$n = n'$
or
![]() $n> n'$
computably in
$n> n'$
computably in
![]() $Y \oplus {X}^{\prime \prime }$
. This will suffice since, applying this repeatedly, we can compute g from
$Y \oplus {X}^{\prime \prime }$
. This will suffice since, applying this repeatedly, we can compute g from
![]() $Y \oplus {X}^{\prime \prime }$
.
$Y \oplus {X}^{\prime \prime }$
.
Using
![]() ${X}^{\prime \prime }$
we can compute
${X}^{\prime \prime }$
we can compute
![]() $\xi = m(\sigma , n')$
and
$\xi = m(\sigma , n')$
and
![]() $r(\sigma , n')$
. If
$r(\sigma , n')$
. If
![]() $n = n'$
then we would have
$n = n'$
then we would have
![]() $f \succ {\theta ^{\xi }_{0}}$
while if
$f \succ {\theta ^{\xi }_{0}}$
while if
![]() $n> n'$
then
$n> n'$
then
![]() $f \succ {\theta ^{\xi }_{k}}, k> 0$
.
$f \succ {\theta ^{\xi }_{k}}, k> 0$
.
If we have
![]() $r(\sigma , n') = \left \ulcorner {\,\not |\,}\right \urcorner $
then that entails
$r(\sigma , n') = \left \ulcorner {\,\not |\,}\right \urcorner $
then that entails
![]() ${\theta ^{\xi ^{-}}_{0}}$
has no e-splitting extensions. Thus, by our supposition f can’t extend
${\theta ^{\xi ^{-}}_{0}}$
has no e-splitting extensions. Thus, by our supposition f can’t extend
![]() ${\theta ^{\xi ^{-}}_{0}}$
, so we can conclude
${\theta ^{\xi ^{-}}_{0}}$
, so we can conclude
![]() $n \neq n'$
.
$n \neq n'$
.
Suppose instead that
![]() $r(\sigma , n') = \left \ulcorner (\uparrow , \hat {n},\hat {m})\right \urcorner $
. In this case, the module
$r(\sigma , n') = \left \ulcorner (\uparrow , \hat {n},\hat {m})\right \urcorner $
. In this case, the module
![]() $\mathcal {S}^{n'}_{e}$
at
$\mathcal {S}^{n'}_{e}$
at
![]() $\xi ^{-}$
must have identified some e-splitting
$\xi ^{-}$
must have identified some e-splitting
![]() $\tau _0, \tau _1$
of
$\tau _0, \tau _1$
of
![]() $ {\theta ^{\xi ^{-}}_{0}}$
and that no
$ {\theta ^{\xi ^{-}}_{0}}$
and that no
![]() ${\theta ^{\xi }_{k}}, k> 0$
has an extension in T which e-splits with either
${\theta ^{\xi }_{k}}, k> 0$
has an extension in T which e-splits with either
![]() $\tau _0$
or
$\tau _0$
or
![]() $\tau _1$
. However, as
$\tau _1$
. However, as
![]() $\Phi _{e}\left (f \oplus X\right )$
is total, if f doesn’t extend either
$\Phi _{e}\left (f \oplus X\right )$
is total, if f doesn’t extend either
![]() $\tau _0$
or
$\tau _0$
or
![]() $\tau _1$
then some initial segment of f must e-split with either
$\tau _1$
then some initial segment of f must e-split with either
![]() $\tau _0$
or
$\tau _0$
or
![]() $\tau _1$
(
$\tau _1$
(
![]() $\Phi _{e}\left (f \oplus X\right )$
can’t agree with incompatible strings). Hence, we can’t have
$\Phi _{e}\left (f \oplus X\right )$
can’t agree with incompatible strings). Hence, we can’t have
![]() $f \succ {\theta ^{\xi }_{k}}, k> 0$
so we must have
$f \succ {\theta ^{\xi }_{k}}, k> 0$
so we must have
![]() $n = n'$
.
$n = n'$
.
This leaves only the case in which
![]() $r(\sigma , n')$
gives one of the incompatible (i.e., e-splitting) outcomes. In this case, we simply test if Y is compatible with
$r(\sigma , n')$
gives one of the incompatible (i.e., e-splitting) outcomes. In this case, we simply test if Y is compatible with
![]() $\Phi _{e}\left ({\theta ^{\xi }_{0}} \oplus X\right )$
. If so, then
$\Phi _{e}\left ({\theta ^{\xi }_{0}} \oplus X\right )$
. If so, then
![]() $n = n'$
. If not, then
$n = n'$
. If not, then
![]() $n> n'$
.
$n> n'$
.
These lemmas, taken together, verify all parts of Proposition 4.1 except 6 which is evident from the construction.
Appendix A Minimality requires double jump
Here we present the promised result about the need for double, rather than single, jump inversion from Section 6.
Proposition 6.1. Given a perfect weakly
![]() $\omega $
-branching pruned f-tree
$\omega $
-branching pruned f-tree
![]() $T \leq _{\mathbf {T}} {\mathbf {0}}'$
one can uniformly construct a computable functional
$T \leq _{\mathbf {T}} {\mathbf {0}}'$
one can uniformly construct a computable functional
![]() $\Phi $
such that e-splitting pairs in T occur above every node in T and for every
$\Phi $
such that e-splitting pairs in T occur above every node in T and for every
![]() $\tau \in \mathrm {rng} T$
there are paths
$\tau \in \mathrm {rng} T$
there are paths
![]() $f \neq g$
extending
$f \neq g$
extending
![]() $\tau $
through T with
$\tau $
through T with
![]() $\Phi _{e}\left (f\right ) = \Phi _{e}\left (g\right )$
.
$\Phi _{e}\left (f\right ) = \Phi _{e}\left (g\right )$
.
Indeed, as remarked in that section, we actually prove a slightly stronger result and show that even if T is unpruned we can start building such paths
![]() $f, g$
above any node
$f, g$
above any node
![]() $\tau \in T$
and maintain agreement under
$\tau \in T$
and maintain agreement under
![]() $\Phi _{e}$
with the only potential for failure being the possibility of hitting a terminal node in T.
$\Phi _{e}$
with the only potential for failure being the possibility of hitting a terminal node in T.
Proof The basic idea of this proof is to use the fact that
![]() $T(\sigma )$
has infinitely many immediate extensions on T to define a limiting behaviour for
$T(\sigma )$
has infinitely many immediate extensions on T to define a limiting behaviour for
![]() $\Phi _{e}\left (\tau \right )$
for
$\Phi _{e}\left (\tau \right )$
for
![]() $\tau \succ T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
for sufficiently large m.
$\tau \succ T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
for sufficiently large m.
Let
![]() $T_{s}$
be a stagewise approximation to T that’s correct in the limit and which doesn’t converge on elements outside the domain. WLOG we may assume that if
$T_{s}$
be a stagewise approximation to T that’s correct in the limit and which doesn’t converge on elements outside the domain. WLOG we may assume that if
![]() $T_s(\sigma ) = \tau $
then
$T_s(\sigma ) = \tau $
then
![]() $\left \ulcorner \sigma \right \urcorner , \left \ulcorner \tau \right \urcorner < s$
and
$\left \ulcorner \sigma \right \urcorner , \left \ulcorner \tau \right \urcorner < s$
and
![]() $T_s(\sigma ')\downarrow $
for all
$T_s(\sigma ')\downarrow $
for all
![]() $\sigma ' \prec \sigma $
. We say that
$\sigma ' \prec \sigma $
. We say that
![]() $T(\sigma )$
was defined at
$T(\sigma )$
was defined at
![]() $s'$
(relative to s) if
$s'$
(relative to s) if
![]() $s' = \mu {t}{\left (\forall t' \in [t, s]\right )\! \left (T_{t'}(\sigma )=T_s(\sigma )\right )}$
and that
$s' = \mu {t}{\left (\forall t' \in [t, s]\right )\! \left (T_{t'}(\sigma )=T_s(\sigma )\right )}$
and that
![]() $\sigma $
is senior to
$\sigma $
is senior to
![]() $\sigma '$
at stage s if
$\sigma '$
at stage s if
![]() $T(\sigma )$
was defined at an earlier stage than
$T(\sigma )$
was defined at an earlier stage than
![]() $T(\sigma ')$
or the same stage and
$T(\sigma ')$
or the same stage and
![]() $\sigma <_L \sigma '$
. We’ll also talk about
$\sigma <_L \sigma '$
. We’ll also talk about
![]() $T(\sigma )$
being senior to
$T(\sigma )$
being senior to
![]() $T(\sigma ')$
when
$T(\sigma ')$
when
![]() $\sigma $
is senior to
$\sigma $
is senior to
![]() $\sigma '$
.
$\sigma '$
.
We first ensure that every non-terminal
![]() $T(\sigma ) = \tau $
is extended by an e-splitting. The idea here is that if
$T(\sigma ) = \tau $
is extended by an e-splitting. The idea here is that if
![]() $\tau ' \succ \tau $
we define
$\tau ' \succ \tau $
we define
![]() $\Phi _{e}\left (\tau '\right )$
to extend
$\Phi _{e}\left (\tau '\right )$
to extend
![]() $\Phi _{e}\left (\tau \right )$
with a guess at the first prior stage that some extension of
$\Phi _{e}\left (\tau \right )$
with a guess at the first prior stage that some extension of
![]() $\tau $
is permanently seen to be
$\tau $
is permanently seen to be
![]() $T( \sigma \widehat {\phantom {x}}\langle m\rangle )$
for some m. Eventually, this guess stabilizes and will differ from the guess that was made along the most senior extension of
$T( \sigma \widehat {\phantom {x}}\langle m\rangle )$
for some m. Eventually, this guess stabilizes and will differ from the guess that was made along the most senior extension of
![]() $\tau $
.
$\tau $
.
Given
![]() $T_s(\sigma ) = \tau $
, define
$T_s(\sigma ) = \tau $
, define
![]() $q_s(\tau ) = t$
where
$q_s(\tau ) = t$
where
![]() $\sigma \widehat {\phantom {x}}\langle m\rangle $
is the most senior immediate extension of
$\sigma \widehat {\phantom {x}}\langle m\rangle $
is the most senior immediate extension of
![]() $\sigma $
relative to s and t the stage it was defined or
$\sigma $
relative to s and t the stage it was defined or
![]() $0$
if no such t exists. We let
$0$
if no such t exists. We let
![]() $q(\tau ) = \lim _{s \to \infty } q_s(\tau )$
. If
$q(\tau ) = \lim _{s \to \infty } q_s(\tau )$
. If
![]() $s = \left \ulcorner \tau \right \urcorner $
we define
$s = \left \ulcorner \tau \right \urcorner $
we define
![]() $\Phi _{e}\left (\tau \right ) = \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q_s(\tau ^{-})\rangle \widehat {\phantom {x}} l_s(\tau ^{-})$
where
$\Phi _{e}\left (\tau \right ) = \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q_s(\tau ^{-})\rangle \widehat {\phantom {x}} l_s(\tau ^{-})$
where
![]() $l_s(\tau )$
is a computable function that will be defined for the second part of the proof.
$l_s(\tau )$
is a computable function that will be defined for the second part of the proof.
Note that, regardless of the behaviour of
![]() $l_s(\tau )$
this guarantees that every non-terminal
$l_s(\tau )$
this guarantees that every non-terminal
![]() $T(\sigma )$
is extended by an e-splitting. Given
$T(\sigma )$
is extended by an e-splitting. Given
![]() $\sigma $
with
$\sigma $
with
![]() $T(\sigma ) = \tau ^{-}$
and
$T(\sigma ) = \tau ^{-}$
and
![]() $\sigma \widehat {\phantom {x}}\langle m\rangle , t$
witnessing that
$\sigma \widehat {\phantom {x}}\langle m\rangle , t$
witnessing that
![]() $q(\tau ^{-}) = t$
we must have
$q(\tau ^{-}) = t$
we must have
![]() $t> \left \ulcorner \sigma \widehat {\phantom {x}}\langle m\rangle \right \urcorner $
. Thus, if
$t> \left \ulcorner \sigma \widehat {\phantom {x}}\langle m\rangle \right \urcorner $
. Thus, if
![]() $\tau \prec T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
we have that
$\tau \prec T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
we have that
![]() $\Phi _{e}\left (\tau \right ) \succ \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q_s(\tau ^{-})\rangle $
for
$\Phi _{e}\left (\tau \right ) \succ \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q_s(\tau ^{-})\rangle $
for
![]() $s = \left \ulcorner \sigma \widehat {\phantom {x}}\langle m\rangle \right \urcorner $
and thus
$s = \left \ulcorner \sigma \widehat {\phantom {x}}\langle m\rangle \right \urcorner $
and thus
![]() $q_s(\tau ^{-}) < q(\tau ^{-})$
. As T is weakly
$q_s(\tau ^{-}) < q(\tau ^{-})$
. As T is weakly
![]() $\omega $
-branching for some sufficiently large
$\omega $
-branching for some sufficiently large
![]() $m'> m$
we have
$m'> m$
we have
![]() $T(\sigma \widehat {\phantom {x}}\langle m'\rangle ) = \tau '$
and
$T(\sigma \widehat {\phantom {x}}\langle m'\rangle ) = \tau '$
and
![]() $ \Phi _{e}\left (\tau '\right ) \succ \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q(\tau ^{-})\rangle $
.
$ \Phi _{e}\left (\tau '\right ) \succ \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q(\tau ^{-})\rangle $
.
We now abstract away from the construction we just performed by noting that we can effectively define a subtree of T consisting of the restriction of T to those nodes of the form
![]() $\sigma \widehat {\phantom {x}}\langle m\rangle $
with
$\sigma \widehat {\phantom {x}}\langle m\rangle $
with
![]() $ \left \ulcorner \sigma \widehat {\phantom {x}}\langle m'\rangle \right \urcorner \geq q(T(\sigma ))$
. On this subtree
$ \left \ulcorner \sigma \widehat {\phantom {x}}\langle m'\rangle \right \urcorner \geq q(T(\sigma ))$
. On this subtree
![]() $q_s(\tau ^{-})$
has achieved its limit anytime it is used to define
$q_s(\tau ^{-})$
has achieved its limit anytime it is used to define
![]() $\Phi _{e}\left (\tau \right )$
. For the remainder of this proof we therefore work on this subtree and (by redefinition) assume that
$\Phi _{e}\left (\tau \right )$
. For the remainder of this proof we therefore work on this subtree and (by redefinition) assume that
![]() $T_s(\sigma ) = \tau $
doesn’t permanently settle on a value until
$T_s(\sigma ) = \tau $
doesn’t permanently settle on a value until
![]() $q_s(\tau ^{-})$
reaches its limit. This allows us to use
$q_s(\tau ^{-})$
reaches its limit. This allows us to use
![]() $\Phi _{e'}\left (\tau ^{-}\right )$
to refer to the value
$\Phi _{e'}\left (\tau ^{-}\right )$
to refer to the value
![]() $ \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q(\tau )\rangle $
and assume that it’s correct at any stage at which
$ \Phi _{e}\left (\tau ^{-}\right )\widehat {\phantom {x}}\langle q(\tau )\rangle $
and assume that it’s correct at any stage at which
![]() $\tau ^{-}$
has permanently entered
$\tau ^{-}$
has permanently entered
![]() $\mathrm {rng} T$
. We can also assume that if
$\mathrm {rng} T$
. We can also assume that if
![]() $T_s(\sigma )\downarrow \neq T_{s+1}(\sigma )$
then
$T_s(\sigma )\downarrow \neq T_{s+1}(\sigma )$
then
![]() $ T_{s+1}(\sigma )\uparrow $
and
$ T_{s+1}(\sigma )\uparrow $
and
![]() $T_{s}(\sigma )$
isn’t extended by any element in
$T_{s}(\sigma )$
isn’t extended by any element in
![]() $\mathrm {rng} T_{s+1}$
.
$\mathrm {rng} T_{s+1}$
.
The idea now is still to pick a limiting behaviour of
![]() $\Phi _{e'}\left (\tau '\right )$
on extensions
$\Phi _{e'}\left (\tau '\right )$
on extensions
![]() $\tau ' \succ T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
for large enough values of m. If we’ve defined some initial segment
$\tau ' \succ T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
for large enough values of m. If we’ve defined some initial segment
![]() $f^{n+1}_\sigma $
of some path through T whose image under
$f^{n+1}_\sigma $
of some path through T whose image under
![]() $\Phi _{e'}$
extends that of
$\Phi _{e'}$
extends that of
![]() $g^{n}_\sigma $
we can control the limiting behaviour of extensions of
$g^{n}_\sigma $
we can control the limiting behaviour of extensions of
![]() $g^{n}_\sigma $
to ensure that we can eventually find some extension
$g^{n}_\sigma $
to ensure that we can eventually find some extension
![]() $ g^{n+1}_\sigma $
whose image under
$ g^{n+1}_\sigma $
whose image under
![]() $\Phi _{e'}$
extends that of
$\Phi _{e'}$
extends that of
![]() $f^{n+1}_\sigma $
. By iterating this, we can build
$f^{n+1}_\sigma $
. By iterating this, we can build
![]() $f_\sigma , g_\sigma $
whose images under
$f_\sigma , g_\sigma $
whose images under
![]() $\Phi _{e'}$
agree.
$\Phi _{e'}$
agree.
We now define (stagewise approximations to) ![]() and specify a computation for
and specify a computation for
![]() $l_s$
to ensure that
$l_s$
to ensure that
![]() $f_\sigma = \bigcup _{n \in \omega } f^{n}_\sigma , g_\sigma = \bigcup _{n \in \omega } g^{n}_\sigma $
are paths whose images agree. Given any
$f_\sigma = \bigcup _{n \in \omega } f^{n}_\sigma , g_\sigma = \bigcup _{n \in \omega } g^{n}_\sigma $
are paths whose images agree. Given any
![]() $\sigma \in \mathrm {dom} T$
with
$\sigma \in \mathrm {dom} T$
with
![]() $T(\sigma )$
not extended by any
$T(\sigma )$
not extended by any
![]() $f_\nu , g_\nu $
, we’ll define
$f_\nu , g_\nu $
, we’ll define
![]() $f^{0}_\sigma , g^{0}_\sigma \succ T(\sigma )$
with common initial segment
$f^{0}_\sigma , g^{0}_\sigma \succ T(\sigma )$
with common initial segment
![]() $T(\sigma )$
. When
$T(\sigma )$
. When
![]() $T_s(\sigma )\downarrow \neq T_{s+1}(\sigma )$
we stipulate that any
$T_s(\sigma )\downarrow \neq T_{s+1}(\sigma )$
we stipulate that any
![]() $\tau ' = T_s(\sigma ')$
for
$\tau ' = T_s(\sigma ')$
for
![]() $\sigma '$
less senior than
$\sigma '$
less senior than
![]() $\sigma $
or
$\sigma $
or
![]() $\sigma ' = \sigma $
are injured. If
$\sigma ' = \sigma $
are injured. If
![]() $\tau $
is injured then we set any
$\tau $
is injured then we set any
![]() $f^{n}_\sigma , g^{n}_\sigma \succeq \tau $
to be undefined and reset
$f^{n}_\sigma , g^{n}_\sigma \succeq \tau $
to be undefined and reset
![]() $l_{s+1}(\tau ) = \langle \rangle $
. Whenever
$l_{s+1}(\tau ) = \langle \rangle $
. Whenever
![]() $f^{n}_\sigma $
(
$f^{n}_\sigma $
(
![]() $g^{n}_\sigma $
) is set to be undefined we also injure
$g^{n}_\sigma $
) is set to be undefined we also injure
![]() $g^{n'}_\sigma $
and
$g^{n'}_\sigma $
and
![]() $f^{n'}_\sigma $
for
$f^{n'}_\sigma $
for
![]() $n' \geq n$
(
$n' \geq n$
(
![]() $f^{n'}_\sigma $
and
$f^{n'}_\sigma $
and
![]() $g^{n'}_\sigma $
for
$g^{n'}_\sigma $
for
![]() $n'> n$
, note the strict inequality here). If we undefine
$n'> n$
, note the strict inequality here). If we undefine
![]() $f^{0}_\sigma $
at stage
$f^{0}_\sigma $
at stage
![]() $ s+1$
then we also injure
$ s+1$
then we also injure
![]() $T_s(\sigma )$
(the plus one ensuring that we injure the node
$T_s(\sigma )$
(the plus one ensuring that we injure the node
![]() $f^{0}_\sigma $
is extending). Finally, we also injure
$f^{0}_\sigma $
is extending). Finally, we also injure
![]() $\tau $
immediately before defining
$\tau $
immediately before defining
![]() $f^{n}_\sigma $
or
$f^{n}_\sigma $
or
![]() $g^n_\sigma $
to be equal to
$g^n_\sigma $
to be equal to
![]() $\tau $
.
$\tau $
.
At stage s we start with
![]() $T_{s}(\langle \rangle )$
and act on nodes in
$T_{s}(\langle \rangle )$
and act on nodes in
![]() $\mathrm {rng} T_{s}$
in order of seniority (which respects
$\mathrm {rng} T_{s}$
in order of seniority (which respects
![]() $\prec $
). Suppose that at stage s we’re taking action on
$\prec $
). Suppose that at stage s we’re taking action on
![]() $\tau = T_{s}(\sigma )$
after having dealt with all more senior and try the following cases in order. Note that, at any time there will only be finitely many
$\tau = T_{s}(\sigma )$
after having dealt with all more senior and try the following cases in order. Note that, at any time there will only be finitely many
![]() $(n, \nu )$
with either
$(n, \nu )$
with either
![]() $f^{n}_\nu $
or
$f^{n}_\nu $
or
![]() $g^{n}_\nu $
defined, so we can computably check whether a case is satisfied for some
$g^{n}_\nu $
defined, so we can computably check whether a case is satisfied for some
![]() $(n, \nu )$
.
$(n, \nu )$
.
-
Case
 $f^{n}_\nu = \tau \land f^{n+1}_\nu \uparrow $
: If
$f^{n}_\nu = \tau \land f^{n+1}_\nu \uparrow $
: If
 $g^{n}_\nu $
is undefined then finish acting for
$g^{n}_\nu $
is undefined then finish acting for
 $\tau $
and all extensions of
$\tau $
and all extensions of
 $\tau $
. Otherwise, ensure
$\tau $
. Otherwise, ensure
 $\Phi _{e'}\left (\tau \right )\widehat {\phantom {x}} l_{s+1}(\tau ) \succ \Phi _{e'}\left (g^{n}_\nu \right )$
. If this is already satisfied by
$\Phi _{e'}\left (\tau \right )\widehat {\phantom {x}} l_{s+1}(\tau ) \succ \Phi _{e'}\left (g^{n}_\nu \right )$
. If this is already satisfied by
 $l_s(\tau )$
then let
$l_s(\tau )$
then let
 $l_{s+1}(\tau ) = l_s(\tau )$
otherwise pick the
$l_{s+1}(\tau ) = l_s(\tau )$
otherwise pick the
 $\prec $
least solution. We’ll inductively ensure that
$\prec $
least solution. We’ll inductively ensure that
 $\Phi _{e'}\left (g^{n}_\nu \right ) \succ \Phi _{e'}\left (f^{n}_\nu \right )$
.
$\Phi _{e'}\left (g^{n}_\nu \right ) \succ \Phi _{e'}\left (f^{n}_\nu \right )$
.Now check if there is any
 $\sigma ' = \sigma \widehat {\phantom {x}}\langle m\rangle $
such that
$\sigma ' = \sigma \widehat {\phantom {x}}\langle m\rangle $
such that
 $T_{s}(\sigma ') = \tau '$
and
$T_{s}(\sigma ') = \tau '$
and
 $\Phi _{e'}\left (\tau '\right ) \succ \Phi _{e'}\left (g^{n}_k\right )$
. If so, take the most senior such
$\Phi _{e'}\left (\tau '\right ) \succ \Phi _{e'}\left (g^{n}_k\right )$
. If so, take the most senior such
 $\sigma '$
and define
$\sigma '$
and define
 $ f^{n+1}_\nu = \tau '$
and continue to the next case. If not, finish processing
$ f^{n+1}_\nu = \tau '$
and continue to the next case. If not, finish processing
 $\tau $
for this stage.
$\tau $
for this stage. -
Case
 $g^{n}_\nu = \tau \land g^{n+1}_\nu \uparrow :$
As above, using
$g^{n}_\nu = \tau \land g^{n+1}_\nu \uparrow :$
As above, using
 $g^{n}_\nu , g^{n+1}_\nu $
in place of
$g^{n}_\nu , g^{n+1}_\nu $
in place of
 $f^{n}_\nu , f^{n+1}_\nu $
and
$f^{n}_\nu , f^{n+1}_\nu $
and
 $f^{n+1}_\nu $
in place of
$f^{n+1}_\nu $
in place of
 $g^{n}_\nu $
(note the off by
$g^{n}_\nu $
(note the off by
 $1$
difference).
$1$
difference). -
Case
 $f^{0}_\sigma \downarrow \land g^{0}_\sigma \uparrow :$
We’ve already done all the hard work when defining
$f^{0}_\sigma \downarrow \land g^{0}_\sigma \uparrow :$
We’ve already done all the hard work when defining
 $f^{0}_\sigma $
, so we look for the most senior
$f^{0}_\sigma $
, so we look for the most senior
 $\tau ' = T_{s}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
with
$\tau ' = T_{s}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
with
 $ \Phi _{e'}\left (f^{0}_\sigma \right ) \preceq \Phi _{e'}\left (\tau '\right )$
and define
$ \Phi _{e'}\left (f^{0}_\sigma \right ) \preceq \Phi _{e'}\left (\tau '\right )$
and define
 $g^{0}_\sigma = \tau '$
. If found, we move on to the next case. If not, finish processing
$g^{0}_\sigma = \tau '$
. If found, we move on to the next case. If not, finish processing
 $\tau $
for this stage.
$\tau $
for this stage. -
Case
 $\left (\forall \nu ,n\right )\!\left (\tau \neq f^{n}_\nu , g^{n}_\nu \right ) \land f^{0}_\sigma \uparrow :$
Let
$\left (\forall \nu ,n\right )\!\left (\tau \neq f^{n}_\nu , g^{n}_\nu \right ) \land f^{0}_\sigma \uparrow :$
Let
 $\tau ' = T_{s}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
with
$\tau ' = T_{s}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
with
 $\sigma \widehat {\phantom {x}}\langle m\rangle $
be the most senior extension of
$\sigma \widehat {\phantom {x}}\langle m\rangle $
be the most senior extension of
 $\sigma $
(if any). If not found then finish processing
$\sigma $
(if any). If not found then finish processing
 $\tau $
for this stage. If found, set
$\tau $
for this stage. If found, set
 $f^{0}_k = \tau '$
and set
$f^{0}_k = \tau '$
and set
 $l_{s+1}(\tau )$
to be the
$l_{s+1}(\tau )$
to be the
 $\prec $
minimal value such that
$\prec $
minimal value such that
 $\Phi _{e'}\left (\tau \right )\widehat {\phantom {x}} l_{s+1}(\tau ) = \Phi _{e'}\left (\tau '\right )$
.
$\Phi _{e'}\left (\tau \right )\widehat {\phantom {x}} l_{s+1}(\tau ) = \Phi _{e'}\left (\tau '\right )$
.
It is straightforward, to verify, that each node in
![]() $\mathrm {rng} T$
is only injured finitely many times and that each
$\mathrm {rng} T$
is only injured finitely many times and that each
![]() $f^{n}_\nu , g^{n}_\nu $
, is only undefined/redefined finitely many times. To see this, note first that once all more senior elements in
$f^{n}_\nu , g^{n}_\nu $
, is only undefined/redefined finitely many times. To see this, note first that once all more senior elements in
![]() $\mathrm {rng} T$
have entered
$\mathrm {rng} T$
have entered
![]() $\mathrm {rng} T$
permanently the only way
$\mathrm {rng} T$
permanently the only way
![]() $\tau $
is injured is if we define
$\tau $
is injured is if we define
![]() $f^{n}_\nu , g^{n}_\nu $
to equal
$f^{n}_\nu , g^{n}_\nu $
to equal
![]() $\tau $
or
$\tau $
or
![]() $\tau = T_s(\nu )$
and
$\tau = T_s(\nu )$
and
![]() $f^0_\nu $
is injured. It is clear from the construction that for at most one pair
$f^0_\nu $
is injured. It is clear from the construction that for at most one pair
![]() $(n,\nu )$
and either f or g do we set
$(n,\nu )$
and either f or g do we set
![]() $f^{n}_\nu , g^{n}_\nu $
to equal
$f^{n}_\nu , g^{n}_\nu $
to equal
![]() $\tau $
and that only if
$\tau $
and that only if
![]() $\tau $
goes unused in this way do we extend it by
$\tau $
goes unused in this way do we extend it by
![]() $ f^{0}_\nu $
. Thus, it is enough to show that each
$ f^{0}_\nu $
. Thus, it is enough to show that each
![]() $f^{n}_\nu , g^{n}_\nu $
eventually settles down. To see this, note that if undefining
$f^{n}_\nu , g^{n}_\nu $
eventually settles down. To see this, note that if undefining
![]() $h^{n}_\nu $
could cause
$h^{n}_\nu $
could cause
![]() $\hat {h}^{n}_\nu $
to become undefined then
$\hat {h}^{n}_\nu $
to become undefined then
![]() $h^{n}_\nu $
took the more senior extension of their common initial segment.
$h^{n}_\nu $
took the more senior extension of their common initial segment.
It is also evident from the construction that the images of
![]() $f_\nu $
and
$f_\nu $
and
![]() $g_\nu $
under
$g_\nu $
under
![]() $e'$
agree. Specifically, that, when defined
$e'$
agree. Specifically, that, when defined
![]() $\Phi _{e}\left (g^{n}_\nu \right ) \succ \Phi _{e}\left (f^{n}_\nu \right )$
and
$\Phi _{e}\left (g^{n}_\nu \right ) \succ \Phi _{e}\left (f^{n}_\nu \right )$
and
![]() $\Phi _{e}\left (f^{n+1}_\nu \right ) \succ \Phi _{e}\left (g^{n}_\nu \right )$
.
$\Phi _{e}\left (f^{n+1}_\nu \right ) \succ \Phi _{e}\left (g^{n}_\nu \right )$
.
We now show that for any
![]() $\sigma \in \mathrm {dom} T$
if
$\sigma \in \mathrm {dom} T$
if
![]() $\tau = T(\sigma )$
isn’t terminal then it is extended. We first deal with the case where
$\tau = T(\sigma )$
isn’t terminal then it is extended. We first deal with the case where
![]() $\tau $
isn’t equal to any
$\tau $
isn’t equal to any
![]() $f^n_\nu $
or
$f^n_\nu $
or
![]() $g^n_\nu $
. In this case, we clearly eventually define
$g^n_\nu $
. In this case, we clearly eventually define
![]() $f^0_\sigma = T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
for some m and then for large enough
$f^0_\sigma = T(\sigma \widehat {\phantom {x}}\langle m\rangle )$
for some m and then for large enough
![]() $m', t$
we will have
$m', t$
we will have
![]() $\tau ' = T_{t}(\sigma \widehat {\phantom {x}}\langle m'\rangle )$
then
$\tau ' = T_{t}(\sigma \widehat {\phantom {x}}\langle m'\rangle )$
then
![]() $\Phi _{e'}\left (\tau '\right ) \succ \Phi _{e'}\left (f^{0}_\sigma \right )$
thus ensuring that we define
$\Phi _{e'}\left (\tau '\right ) \succ \Phi _{e'}\left (f^{0}_\sigma \right )$
thus ensuring that we define
![]() $g^0_\sigma $
.
$g^0_\sigma $
.
If
![]() $\tau = f^{n+1}_\nu = T_{s+1}(\sigma )$
the agreement remarked on above ensures we eventually get a chance to define
$\tau = f^{n+1}_\nu = T_{s+1}(\sigma )$
the agreement remarked on above ensures we eventually get a chance to define
![]() $l_{s+1}(\tau )$
so that
$l_{s+1}(\tau )$
so that
![]() $\Phi _{e'}\left (f^{n}_\nu \right )\widehat {\phantom {x}} l_{s+1}(\tau ) \succ \Phi _{e'}\left (g^{n+1}_\nu \right )$
after which
$\Phi _{e'}\left (f^{n}_\nu \right )\widehat {\phantom {x}} l_{s+1}(\tau ) \succ \Phi _{e'}\left (g^{n+1}_\nu \right )$
after which
![]() $\tau $
is never injured. Thus, for some sufficiently large
$\tau $
is never injured. Thus, for some sufficiently large
![]() $m,t$
we have that if
$m,t$
we have that if
![]() $\tau ' = T_{t}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
then
$\tau ' = T_{t}(\sigma \widehat {\phantom {x}}\langle m\rangle )$
then
![]() $\Phi _{e'}\left (\tau '\right ) \succ \Phi _{e'}\left (g^{n}_\nu \right )$
and we eventually define
$\Phi _{e'}\left (\tau '\right ) \succ \Phi _{e'}\left (g^{n}_\nu \right )$
and we eventually define
![]() $f^{n+2}_\nu $
to be equal to such a
$f^{n+2}_\nu $
to be equal to such a
![]() $\tau '$
. The same argument applies, with the obvious adjustments to the indexes, when
$\tau '$
. The same argument applies, with the obvious adjustments to the indexes, when
![]() $\tau = g^{n}_\nu $
.
$\tau = g^{n}_\nu $
.
Thus, if our tree is pruned then, as it is weakly,
![]() $\omega $
branching for any
$\omega $
branching for any
![]() $\sigma \in \mathrm {dom} T$
there is some m with
$\sigma \in \mathrm {dom} T$
there is some m with
![]() $\sigma '=\sigma \widehat {\phantom {x}}\langle m\rangle $
such that
$\sigma '=\sigma \widehat {\phantom {x}}\langle m\rangle $
such that
![]() $f_{\sigma '}, g_{\sigma '}$
are defined and extend
$f_{\sigma '}, g_{\sigma '}$
are defined and extend
![]() $ T(\sigma ')$
with equal images under
$ T(\sigma ')$
with equal images under
![]() $\Phi _{e}$
. The moreover claim is straightforward as well.
$\Phi _{e}$
. The moreover claim is straightforward as well.
With slightly more care, we could ensure that every node
![]() $\tau \in \mathrm {rng} T$
was extended by infinitely many paths
$\tau \in \mathrm {rng} T$
was extended by infinitely many paths
![]() $f_{k, \tau }, g_{k, \tau }$
. We are unsure if this argument can be improved to construct a single total computable functional which witnesses all
$f_{k, \tau }, g_{k, \tau }$
. We are unsure if this argument can be improved to construct a single total computable functional which witnesses all
![]() ${\mathbf {0}}'$
computable f-trees fail, in a strong sense, to have the properties necessary to help in a minimality style argument.
${\mathbf {0}}'$
computable f-trees fail, in a strong sense, to have the properties necessary to help in a minimality style argument.
Appendix B Ordinal notation technicalities
If we wish to build a sequence of trees
![]() $T_n$
all homeomorphic to
$T_n$
all homeomorphic to
![]() $T_\omega $
ensuring the homeomorphism at limit levels only requires that we ensure
$T_\omega $
ensuring the homeomorphism at limit levels only requires that we ensure
![]() $T_n{{\restriction _{n}}} = T_\omega {{\restriction _{n}}}$
and that our homeomorphism from
$T_n{{\restriction _{n}}} = T_\omega {{\restriction _{n}}}$
and that our homeomorphism from
![]() $ T_{n+1}$
to
$ T_{n+1}$
to
![]() $T_n$
is the identity on
$T_n$
is the identity on
![]() $T_n{{\restriction _{n}}}$
. In this appendix, we show that this idea can be extended to arbitrary ordinal notations. The potential difficulty here is that we attempt to demand that
$T_n{{\restriction _{n}}}$
. In this appendix, we show that this idea can be extended to arbitrary ordinal notations. The potential difficulty here is that we attempt to demand that
![]() $ T_{\beta _n}{{\restriction _{n}}}$
should equal
$ T_{\beta _n}{{\restriction _{n}}}$
should equal
![]() $T_\lambda {{\restriction _{n}}}$
and that for some
$T_\lambda {{\restriction _{n}}}$
and that for some
![]() $\gamma $
with
$\gamma $
with
![]() $\beta _n <_{\mathcal {O}} \gamma <_{\mathcal {O}} \lambda $
we also demand
$\beta _n <_{\mathcal {O}} \gamma <_{\mathcal {O}} \lambda $
we also demand
![]() $T_\gamma {{\restriction _{{m}}}} = T_{\lambda '}$
for some
$T_\gamma {{\restriction _{{m}}}} = T_{\lambda '}$
for some
![]() $\lambda '>_{\mathcal {O}} \lambda , m > n$
.
$\lambda '>_{\mathcal {O}} \lambda , m > n$
.
From here on out, we assume that we are working below some limit notation
![]() $\alpha $
(e.g.,
$\alpha $
(e.g.,
![]() $T_\alpha $
is the top tree) and show that for all
$T_\alpha $
is the top tree) and show that for all
![]() $\beta \leq _{\mathcal {O}} \alpha $
we can effectively define
$\beta \leq _{\mathcal {O}} \alpha $
we can effectively define
![]() ${\beta }^{\Diamond }$
and
${\beta }^{\Diamond }$
and
![]() $ l^{\Diamond }(\beta )$
. The idea is that
$ l^{\Diamond }(\beta )$
. The idea is that
![]() $T_\beta $
will copy strings of length
$T_\beta $
will copy strings of length
![]() $l^{\Diamond }(\beta )$
from the tree
$l^{\Diamond }(\beta )$
from the tree
![]() $T_{{\beta }^{\Diamond }}$
. Note that,
$T_{{\beta }^{\Diamond }}$
. Note that,
![]() ${\beta }^{\Diamond }$
and
${\beta }^{\Diamond }$
and
![]() $l^{\Diamond }(\beta )$
will depend on both
$l^{\Diamond }(\beta )$
will depend on both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. We start by making the following definition.
$\beta $
. We start by making the following definition.
Definition B.1. An
![]() $\mathcal {O}$
-path is a non-empty string
$\mathcal {O}$
-path is a non-empty string
![]() $\delta \in \omega ^{<\omega }$
that satisfies the following for all
$\delta \in \omega ^{<\omega }$
that satisfies the following for all
![]() $n + 1 \in \mathrm {dom} \delta , \kappa \in \mathcal {O}$
and some
$n + 1 \in \mathrm {dom} \delta , \kappa \in \mathcal {O}$
and some
![]() $\beta \in \mathcal {O}$
:
$\beta \in \mathcal {O}$
:
-
1.
 $\delta (\left \lvert \delta \right \rvert - 1) = \beta $
.
$\delta (\left \lvert \delta \right \rvert - 1) = \beta $
. -
2. If
 $\delta (n) = \kappa + 1$
then
$\delta (n) = \kappa + 1$
then
 $\delta (n+1) = \kappa $
.
$\delta (n+1) = \kappa $
. -
3. If
 $\delta (n) = \lambda $
and the notation
$\delta (n) = \lambda $
and the notation
 $\lambda $
isn’t a successor then
$\lambda $
isn’t a successor then
 $\delta (n+1) = \gamma \in \mathrm {rng} {\left \{ \lambda \right \}}^{\mathcal {O}}$
.
$\delta (n+1) = \gamma \in \mathrm {rng} {\left \{ \lambda \right \}}^{\mathcal {O}}$
.
We call such an
![]() $\mathcal {O}$
-path an
$\mathcal {O}$
-path an
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\delta (0)$
to
$\delta (0)$
to
![]() $\beta $
. The
$\beta $
. The
![]() $\mathcal {O}$
-path is minimal if the
$\mathcal {O}$
-path is minimal if the
![]() $\gamma $
in 3 is required to be the minimal element in
$\gamma $
in 3 is required to be the minimal element in
![]() $\mathrm {rng} {\left \{ \lambda \right \}}^{\mathcal {O}}$
with
$\mathrm {rng} {\left \{ \lambda \right \}}^{\mathcal {O}}$
with
![]() $\beta \leq _{\mathcal {O}} \gamma $
.
$\beta \leq _{\mathcal {O}} \gamma $
.
Lemma B.2. If
![]() $\beta \leq _{\mathcal {O}} \alpha $
then there is a unique minimal
$\beta \leq _{\mathcal {O}} \alpha $
then there is a unique minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
. Moreover, if
$\beta $
. Moreover, if
![]() $\delta $
is a minimal
$\delta $
is a minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
then
$\beta $
then
![]() $\delta {{\restriction _{n}}}, n>0$
is the minimal
$\delta {{\restriction _{n}}}, n>0$
is the minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\delta (n -1)$
.
$\delta (n -1)$
.
Proof Clearly, no initial segment of an
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
can be an
$\beta $
can be an
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
as an
$\beta $
as an
![]() $\mathcal {O}$
-path is a strictly decreasing sequence under
$\mathcal {O}$
-path is a strictly decreasing sequence under
![]() $<_{\mathcal {O}}$
. Moreover, there is at most one minimal
$<_{\mathcal {O}}$
. Moreover, there is at most one minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
as a minimal
$\beta $
as a minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
is the lexicographically least
$\beta $
is the lexicographically least
![]() $\mathcal {O}$
-path (under
$\mathcal {O}$
-path (under
![]() $<_{\mathcal {O}}$
) from
$<_{\mathcal {O}}$
) from
![]() $\alpha $
to
$\alpha $
to
![]() $ \beta $
. This establishes the uniqueness and implies the moreover claim as well. It only remains to show that there is always such an
$ \beta $
. This establishes the uniqueness and implies the moreover claim as well. It only remains to show that there is always such an
![]() $\mathcal {O}$
-path.
$\mathcal {O}$
-path.
Suppose not, then let
![]() $f(0) = \alpha $
and define
$f(0) = \alpha $
and define
![]() $f(n+1)$
as per the definition of a minimal
$f(n+1)$
as per the definition of a minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
. If we ever have
$\beta $
. If we ever have
![]() $f(n) = \beta $
then
$f(n) = \beta $
then
![]() $f{{\restriction _{{n+1}}}}$
is a minimal
$f{{\restriction _{{n+1}}}}$
is a minimal
![]() $ \mathcal {O}$
-path from
$ \mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
. If not, then, inductively,
$\beta $
. If not, then, inductively,
![]() $f(n)>_{\mathcal {O}} \beta $
and the conditions provide a unique definition for
$f(n)>_{\mathcal {O}} \beta $
and the conditions provide a unique definition for
![]() $f(n+1)$
. Thus, f is an infinite descending sequence of notations. Contradiction.
$f(n+1)$
. Thus, f is an infinite descending sequence of notations. Contradiction.
Definition B.3. We inductively define
![]() $l^{\Diamond }(\beta ), {\beta }^{\Diamond }$
for
$l^{\Diamond }(\beta ), {\beta }^{\Diamond }$
for
![]() $\beta <_{\mathcal {O}} \alpha $
as follows.
$\beta <_{\mathcal {O}} \alpha $
as follows.
Let
![]() $\delta $
be the minimal
$\delta $
be the minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
,
$\beta $
,
![]() $n = \left \lvert \delta \right \rvert $
and
$n = \left \lvert \delta \right \rvert $
and
![]() $\gamma = \delta (n - 2)$
. We stipulate that
$\gamma = \delta (n - 2)$
. We stipulate that
![]() $l^{\Diamond }(\alpha ) =0$
and break our definition into the following cases.
$l^{\Diamond }(\alpha ) =0$
and break our definition into the following cases.
-
Case
 $\gamma \in {}^{+}{\mathcal {O}}:$
Define
$\gamma \in {}^{+}{\mathcal {O}}:$
Define
 $l^{\Diamond }(\beta ) = l^{\Diamond }(\gamma )$
. If
$l^{\Diamond }(\beta ) = l^{\Diamond }(\gamma )$
. If
 $\gamma $
is an even notation then define
$\gamma $
is an even notation then define
 ${\beta }^{\Diamond } = \gamma $
and otherwise define
${\beta }^{\Diamond } = \gamma $
and otherwise define
 ${\beta }^{\Diamond } = {\gamma }^{\Diamond }$
.
${\beta }^{\Diamond } = {\gamma }^{\Diamond }$
. -
Case
 $\gamma \in \overrightarrow {\mathcal {O}}: $
Let
$\gamma \in \overrightarrow {\mathcal {O}}: $
Let
 $m \in \omega $
be such that
$m \in \omega $
be such that
 $\beta = {\left \{\gamma \right \}}^{\mathcal {O}}(m)$
. Define
$\beta = {\left \{\gamma \right \}}^{\mathcal {O}}(m)$
. Define
 ${\beta }^{\Diamond } = \gamma $
and
${\beta }^{\Diamond } = \gamma $
and
 $l^{\Diamond }(\beta ) = l^{\Diamond }(\gamma ) + m$
.
$l^{\Diamond }(\beta ) = l^{\Diamond }(\gamma ) + m$
.
Lemma B.4. If
![]() $\lambda \in \overrightarrow {\mathcal {O}}, \lambda \leq _{\mathcal {O}} \alpha $
, and
$\lambda \in \overrightarrow {\mathcal {O}}, \lambda \leq _{\mathcal {O}} \alpha $
, and
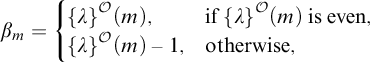 $$\begin{align*}\beta_m = \begin{cases} {\left\{ \lambda \right\}}^{\mathcal{O}}(m), & \text{if } {\left\{ \lambda \right\}}^{\mathcal{O}}(m) \text{ is even,} \\ {\left\{ \lambda \right\}}^{\mathcal{O}}(m) - 1, & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\beta_m = \begin{cases} {\left\{ \lambda \right\}}^{\mathcal{O}}(m), & \text{if } {\left\{ \lambda \right\}}^{\mathcal{O}}(m) \text{ is even,} \\ {\left\{ \lambda \right\}}^{\mathcal{O}}(m) - 1, & \text{otherwise,} \end{cases} \end{align*}$$
then for all sufficiently large m,
![]() ${\beta _m}^{\Diamond } = \lambda $
and
${\beta _m}^{\Diamond } = \lambda $
and
![]() $l^{\Diamond }(\beta _m) \geq m$
.
$l^{\Diamond }(\beta _m) \geq m$
.
Proof Let
![]() $\delta _m$
be the minimal
$\delta _m$
be the minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta _m$
. We first establish that for all sufficiently large m we have
$\beta _m$
. We first establish that for all sufficiently large m we have
![]() $\lambda \in \mathrm {rng} \delta _m$
.
$\lambda \in \mathrm {rng} \delta _m$
.
Note that, by examination of the conditions from Definition B.1, if
![]() $\delta _n(k) = \kappa \geq _{\mathcal {O}} \lambda $
then we clearly have that
$\delta _n(k) = \kappa \geq _{\mathcal {O}} \lambda $
then we clearly have that
![]() $\delta _n{{\restriction _{{k+1}}}} \prec \delta _m$
for
$\delta _n{{\restriction _{{k+1}}}} \prec \delta _m$
for
![]() $m \geq n$
(as
$m \geq n$
(as
![]() $\kappa $
clearly satisfies the minimality requirement for
$\kappa $
clearly satisfies the minimality requirement for
![]() $\delta _m$
). Thus, if we see
$\delta _m$
). Thus, if we see
![]() $\lambda \in \mathrm {rng} \delta _n$
for any n, we are done, so suppose this never happens.
$\lambda \in \mathrm {rng} \delta _n$
for any n, we are done, so suppose this never happens.
Define
![]() $f(k)$
to be equal to
$f(k)$
to be equal to
![]() $\delta _n(k)$
for the least value n such that
$\delta _n(k)$
for the least value n such that
![]() $\delta _{n}(k)>_{\mathcal {O}} \lambda $
. Obviously,
$\delta _{n}(k)>_{\mathcal {O}} \lambda $
. Obviously,
![]() $f(0)$
is defined, so suppose that
$f(0)$
is defined, so suppose that
![]() $f(k+1)$
fails to be defined for some minimal k. If
$f(k+1)$
fails to be defined for some minimal k. If
![]() $ f(k)$
was a successor ordinal then
$ f(k)$
was a successor ordinal then
![]() $\delta _{m}(k+1) = \lambda $
where m is the witness defining
$\delta _{m}(k+1) = \lambda $
where m is the witness defining
![]() $f(k)$
contradicting the supposition. Thus, we can assume that
$f(k)$
contradicting the supposition. Thus, we can assume that
![]() $f(k) = \kappa \in \overrightarrow {\mathcal {O}}$
. But, if
$f(k) = \kappa \in \overrightarrow {\mathcal {O}}$
. But, if
![]() $ {\left \{\kappa \right \}}^{\mathcal {O}}(x) \leq _{\mathcal {O}} \lambda $
for all x then we’d have
$ {\left \{\kappa \right \}}^{\mathcal {O}}(x) \leq _{\mathcal {O}} \lambda $
for all x then we’d have
![]() $\kappa \leq _{\mathcal {O}} \lambda $
contradicting our assumption. Thus, we can pick x maximal with
$\kappa \leq _{\mathcal {O}} \lambda $
contradicting our assumption. Thus, we can pick x maximal with
![]() ${\left \{\kappa \right \}}^{\mathcal {O}}(x) <_{\mathcal {O}} \lambda $
and then choose n so that
${\left \{\kappa \right \}}^{\mathcal {O}}(x) <_{\mathcal {O}} \lambda $
and then choose n so that
![]() $ {\left \{ \lambda \right \}}^{\mathcal {O}}(n)>_{\mathcal {O}} {\left \{\kappa \right \}}^{\mathcal {O}}(x)$
. Therefore,
$ {\left \{ \lambda \right \}}^{\mathcal {O}}(n)>_{\mathcal {O}} {\left \{\kappa \right \}}^{\mathcal {O}}(x)$
. Therefore,
![]() $\delta _{n}(k+1) \geq _{\mathcal {O}} {\left \{\kappa \right \}}^{\mathcal {O}}(x+1) \geq _{\mathcal {O}} \lambda $
and, by assumption, we can’t have equality showing that
$\delta _{n}(k+1) \geq _{\mathcal {O}} {\left \{\kappa \right \}}^{\mathcal {O}}(x+1) \geq _{\mathcal {O}} \lambda $
and, by assumption, we can’t have equality showing that
![]() $f(k+1)$
is defined. But the function f defines an infinite decreasing sequence of notations. Contradiction. Therefore, for all sufficiently large m we must have
$f(k+1)$
is defined. But the function f defines an infinite decreasing sequence of notations. Contradiction. Therefore, for all sufficiently large m we must have
![]() $\lambda \in \mathrm {rng} \delta _m$
.
$\lambda \in \mathrm {rng} \delta _m$
.
If
![]() $\lambda \in \mathrm {rng} \delta _m$
then we obviously have
$\lambda \in \mathrm {rng} \delta _m$
then we obviously have
![]() $\beta _m = \delta (\left \lvert \delta \right \rvert - 1)$
and either
$\beta _m = \delta (\left \lvert \delta \right \rvert - 1)$
and either
![]() $\lambda = \delta (\left \lvert \delta \right \rvert - 2)$
if
$\lambda = \delta (\left \lvert \delta \right \rvert - 2)$
if
![]() $\beta _m = {\left \{ \lambda \right \}}^{\mathcal {O}}(m)$
or
$\beta _m = {\left \{ \lambda \right \}}^{\mathcal {O}}(m)$
or
![]() $\lambda = \delta (\left \lvert \delta \right \rvert - 3), {\left \{ \lambda \right \}}^{\mathcal {O}}(m) = \beta _m + 1 = \delta (\left \lvert \delta \right \rvert - 2)$
. In both cases, we clearly have
$\lambda = \delta (\left \lvert \delta \right \rvert - 3), {\left \{ \lambda \right \}}^{\mathcal {O}}(m) = \beta _m + 1 = \delta (\left \lvert \delta \right \rvert - 2)$
. In both cases, we clearly have
![]() ${\beta _m}^{\Diamond } = \lambda $
and
${\beta _m}^{\Diamond } = \lambda $
and
![]() $l^{\Diamond }(\beta _m) \geq m$
.
$l^{\Diamond }(\beta _m) \geq m$
.
Proposition B.5. Suppose that for all
![]() $\beta \leq _{\mathcal {O}} \alpha $
we have
$\beta \leq _{\mathcal {O}} \alpha $
we have
![]() $T_\beta {{\restriction _{{l^{\Diamond }(\beta )}}}} = \tilde {T}_{{\beta }^{\Diamond }}{{\restriction _{{l^{\Diamond }(\beta )}}}}$
where
$T_\beta {{\restriction _{{l^{\Diamond }(\beta )}}}} = \tilde {T}_{{\beta }^{\Diamond }}{{\restriction _{{l^{\Diamond }(\beta )}}}}$
where
![]() $\tilde {T}_\kappa \supset T_\kappa $
for all
$\tilde {T}_\kappa \supset T_\kappa $
for all
![]() $\kappa $
then all of the following hold:
$\kappa $
then all of the following hold:
-
1.
 ${\beta }^{\Diamond }, l^{\Diamond }(\beta )$
are given by a computable function of
${\beta }^{\Diamond }, l^{\Diamond }(\beta )$
are given by a computable function of
 $\alpha , \beta $
.
$\alpha , \beta $
. -
2. For all
 $\beta <_{\mathcal {O}} \alpha $
,
$\beta <_{\mathcal {O}} \alpha $
,
 ${\beta }^{\Diamond }$
is an even notation satisfying
${\beta }^{\Diamond }$
is an even notation satisfying
 $\beta <_{\mathcal {O}} {\beta }^{\Diamond } \leq _{\mathcal {O}} \alpha $
.
$\beta <_{\mathcal {O}} {\beta }^{\Diamond } \leq _{\mathcal {O}} \alpha $
. -
3. If
 $\beta <_{\mathcal {O}} \kappa <_{\mathcal {O}} {\beta }^{\Diamond }$
then
$\beta <_{\mathcal {O}} \kappa <_{\mathcal {O}} {\beta }^{\Diamond }$
then
 $T_\kappa {{\restriction _{{l^{\Diamond }(\beta )}}}} \supset \tilde {T}_{{\beta }^{\Diamond }}{{\restriction _{{l^{\Diamond }(\beta )}}}}$
and
$T_\kappa {{\restriction _{{l^{\Diamond }(\beta )}}}} \supset \tilde {T}_{{\beta }^{\Diamond }}{{\restriction _{{l^{\Diamond }(\beta )}}}}$
and
 $l^{\Diamond }(\kappa ) \geq l^{\Diamond }(\beta )$
. Furthermore, if we always have
$l^{\Diamond }(\kappa ) \geq l^{\Diamond }(\beta )$
. Furthermore, if we always have
 $T_{\beta }^{\langle \infty \rangle } {{\restriction _{{l^{\Diamond }(\beta )}}}} = {\tilde {T}}_{{\beta }^{\Diamond }}^{\langle \infty \rangle } {{\restriction _{{l^{\Diamond }(\beta )}}}}$
then
$T_{\beta }^{\langle \infty \rangle } {{\restriction _{{l^{\Diamond }(\beta )}}}} = {\tilde {T}}_{{\beta }^{\Diamond }}^{\langle \infty \rangle } {{\restriction _{{l^{\Diamond }(\beta )}}}}$
then
 ${{T_\kappa }^{\langle \infty \rangle }} {{\restriction _{{l^{\Diamond }(\beta )}}}} = {{\tilde {T}}_{{\beta }^{\Diamond }}^{\langle \infty \rangle }} {{\restriction _{{l^{\Diamond }(\beta )}}}}$
.
${{T_\kappa }^{\langle \infty \rangle }} {{\restriction _{{l^{\Diamond }(\beta )}}}} = {{\tilde {T}}_{{\beta }^{\Diamond }}^{\langle \infty \rangle }} {{\restriction _{{l^{\Diamond }(\beta )}}}}$
. -
4. If
 $\lambda \leq _{\mathcal {O}} \alpha $
is a limit notation then we can computably (in
$\lambda \leq _{\mathcal {O}} \alpha $
is a limit notation then we can computably (in
 $\lambda , n, \alpha $
) enumerate a sequence of even notations
$\lambda , n, \alpha $
) enumerate a sequence of even notations
 $\beta _n <_{\mathcal {O}} \lambda $
with
$\beta _n <_{\mathcal {O}} \lambda $
with
 $ {\beta _n}^{\Diamond } = \lambda $
such that both
$ {\beta _n}^{\Diamond } = \lambda $
such that both
 $\beta _n$
and
$\beta _n$
and
 $l^{\Diamond }(\beta _n) \geq n$
are strictly monotonically increasing.
$l^{\Diamond }(\beta _n) \geq n$
are strictly monotonically increasing.
Proof The computability is clear from the definition establishing 1. To verify 2 note that if
![]() ${\beta }^{\Diamond }$
was going to be an odd notation then we set
${\beta }^{\Diamond }$
was going to be an odd notation then we set
![]() $ {\beta }^{\Diamond } = {\gamma }^{\Diamond }$
which guarantees that
$ {\beta }^{\Diamond } = {\gamma }^{\Diamond }$
which guarantees that
![]() ${\beta }^{\Diamond }$
is even. As the only elements that can appear in a minimal
${\beta }^{\Diamond }$
is even. As the only elements that can appear in a minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
are
$\beta $
are
![]() $\leq _{\mathcal {O}}$
$\leq _{\mathcal {O}}$
![]() $\alpha $
this establishes the other part of this claim.
$\alpha $
this establishes the other part of this claim.
To verify 3 suppose that
![]() $\beta <_{\mathcal {O}} \kappa <_{\mathcal {O}} {\beta }^{\Diamond }$
,
$\beta <_{\mathcal {O}} \kappa <_{\mathcal {O}} {\beta }^{\Diamond }$
,
![]() $\delta $
is a minimal
$\delta $
is a minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\beta $
, and
$\beta $
, and
![]() $\gamma = \delta (\left \lvert \delta \right \rvert - 2)$
. WLOG we may assume that
$\gamma = \delta (\left \lvert \delta \right \rvert - 2)$
. WLOG we may assume that
![]() $\gamma = {\beta }^{\Diamond }$
since otherwise
$\gamma = {\beta }^{\Diamond }$
since otherwise
![]() $\gamma $
is an odd notation and the claim for
$\gamma $
is an odd notation and the claim for
![]() $\beta $
follows by proving the claim for
$\beta $
follows by proving the claim for
![]() $\gamma $
. If
$\gamma $
. If
![]() $\delta '$
is a minimal
$\delta '$
is a minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $ \alpha $
to
$ \alpha $
to
![]() $\kappa $
then
$\kappa $
then
![]() $\delta ' \succ \delta ^{-}$
since
$\delta ' \succ \delta ^{-}$
since
![]() $\delta ^{-}$
is the minimal
$\delta ^{-}$
is the minimal
![]() $\mathcal {O}$
-path from
$\mathcal {O}$
-path from
![]() $\alpha $
to
$\alpha $
to
![]() $\gamma = {\beta }^{\Diamond }>_{\mathcal {O}} \kappa $
.
$\gamma = {\beta }^{\Diamond }>_{\mathcal {O}} \kappa $
.
But if
![]() $\kappa '$
appears in
$\kappa '$
appears in
![]() $\mathrm {rng}\ \delta ' \setminus \mathrm {rng}\ \delta ^{-}$
then we must have
$\mathrm {rng}\ \delta ' \setminus \mathrm {rng}\ \delta ^{-}$
then we must have
![]() $T_{\kappa '}{{\restriction _{{l^{\Diamond }(\beta )} }}} \supset \tilde {T}_{\gamma }{{\restriction _{{l^{\Diamond }(\beta )}}}}$
and
$T_{\kappa '}{{\restriction _{{l^{\Diamond }(\beta )} }}} \supset \tilde {T}_{\gamma }{{\restriction _{{l^{\Diamond }(\beta )}}}}$
and
![]() $l^{\Diamond }(\kappa ') \geq l^{\Diamond }(\beta )$
(by induction on
$l^{\Diamond }(\kappa ') \geq l^{\Diamond }(\beta )$
(by induction on
![]() $n \in \mathrm {dom}\ \delta ' \setminus \mathrm {dom}\ \delta ^{-}$
). A similar argument shows the equality claim for the pruned trees under the provided assumptions.
$n \in \mathrm {dom}\ \delta ' \setminus \mathrm {dom}\ \delta ^{-}$
). A similar argument shows the equality claim for the pruned trees under the provided assumptions.
Finally, for 4 let
![]() $\beta ^{\prime }_n$
be the sequence defined in Lemma B.4 and inductively define
$\beta ^{\prime }_n$
be the sequence defined in Lemma B.4 and inductively define
![]() $\beta _{n+1}$
to be the first element
$\beta _{n+1}$
to be the first element
![]() $\beta ^{\prime }_m$
with
$\beta ^{\prime }_m$
with
![]() ${\beta ^{\prime }_m}^{\Diamond } = \lambda $
and (when
${\beta ^{\prime }_m}^{\Diamond } = \lambda $
and (when
![]() $n> 0$
)
$n> 0$
)
![]() $l^{\Diamond }(\beta ^{\prime }_m)> l^{\Diamond }(\beta _n), \beta ^{\prime }_m >_{\mathcal {O}} \beta _n$
. Clearly, we can computably search for such an element and Lemma B.4 ensures that one will always be found. The moreover claim follows immediately from 3.
$l^{\Diamond }(\beta ^{\prime }_m)> l^{\Diamond }(\beta _n), \beta ^{\prime }_m >_{\mathcal {O}} \beta _n$
. Clearly, we can computably search for such an element and Lemma B.4 ensures that one will always be found. The moreover claim follows immediately from 3.
Lemma B.6. Given a notation
![]() $\lambda \in \overrightarrow {\mathcal {O}}$
and a tree
$\lambda \in \overrightarrow {\mathcal {O}}$
and a tree
![]() $T_\lambda \subset \omega ^{<\omega }$
computable in
$T_\lambda \subset \omega ^{<\omega }$
computable in
![]() ${{X}^{(\lambda )}}$
we can produce a tree
${{X}^{(\lambda )}}$
we can produce a tree
![]() $\tilde {T}_\lambda \supset T_\lambda $
with
$\tilde {T}_\lambda \supset T_\lambda $
with
![]() $[\tilde {T}_\lambda ] = [T_\lambda ]$
such that for all
$[\tilde {T}_\lambda ] = [T_\lambda ]$
such that for all
![]() $\beta <_{\mathcal {O}} \lambda $
if
$\beta <_{\mathcal {O}} \lambda $
if
![]() ${\beta }^{\Diamond } = \lambda $
then
${\beta }^{\Diamond } = \lambda $
then
![]() $\tilde {T}_\lambda {{\restriction _{{l^{\Diamond }(\beta )}}}}$
is uniformly computable in
$\tilde {T}_\lambda {{\restriction _{{l^{\Diamond }(\beta )}}}}$
is uniformly computable in
![]() ${{X}^{(\beta )}}$
. Moreover, this holds with all possible uniformity and is agnostic to the index for
${{X}^{(\beta )}}$
. Moreover, this holds with all possible uniformity and is agnostic to the index for
![]() $T_\lambda $
.
$T_\lambda $
.
Uniformly computable here specifically means there is a computable functional
![]() $\Xi $
with
$\Xi $
with
![]() $\Xi (\beta , {{X}^{(\beta )}}, \sigma )$
deciding the membership of
$\Xi (\beta , {{X}^{(\beta )}}, \sigma )$
deciding the membership of
![]() $\sigma $
in
$\sigma $
in
![]() $\tilde {T}_\lambda $
when
$\tilde {T}_\lambda $
when
![]() ${\beta }^{\Diamond } = \lambda $
and
${\beta }^{\Diamond } = \lambda $
and
![]() $\lvert \sigma \rvert \leq l^{\Diamond }(\beta )$
and that an index for
$\lvert \sigma \rvert \leq l^{\Diamond }(\beta )$
and that an index for
![]() $\Xi $
is computable from
$\Xi $
is computable from
![]() $\lambda $
and an index for
$\lambda $
and an index for
![]() $T_\lambda $
.
$T_\lambda $
.
Proof By part 4 of Proposition B.5 let
![]() $\beta _n$
be a monotonically increasing computable enumeration of the notations
$\beta _n$
be a monotonically increasing computable enumeration of the notations
![]() $\beta $
with
$\beta $
with
![]() ${\beta }^{\Diamond } = \lambda $
and
${\beta }^{\Diamond } = \lambda $
and
![]() $l_n = l^{\Diamond }(\beta _n)$
also monotonically increasing with limit
$l_n = l^{\Diamond }(\beta _n)$
also monotonically increasing with limit
![]() $\omega $
.
$\omega $
.
We now define
![]() $\tilde {T}_\lambda $
by setting
$\tilde {T}_\lambda $
by setting
![]() $\sigma \notin \tilde {T}_\lambda $
where n is the greatest with
$\sigma \notin \tilde {T}_\lambda $
where n is the greatest with
![]() $\lvert \sigma \rvert \geq l_{n+1}$
just if we see a computation whose use is seen to be limited to
$\lvert \sigma \rvert \geq l_{n+1}$
just if we see a computation whose use is seen to be limited to
![]() $ {{X}^{({\beta _n})}}$
before stage n placing some
$ {{X}^{({\beta _n})}}$
before stage n placing some
![]() $\sigma ' \prec \sigma $
out of
$\sigma ' \prec \sigma $
out of
![]() $T_\lambda $
. Otherwise, place
$T_\lambda $
. Otherwise, place
![]() $\sigma $
into
$\sigma $
into
![]() $\tilde {T}_\lambda $
. By seen to be limited to, we mean that the computation only consults columns
$\tilde {T}_\lambda $
. By seen to be limited to, we mean that the computation only consults columns
![]() $\kappa $
of
$\kappa $
of
![]() ${{X}^{({\lambda })}}$
which are enumerated to be below some
${{X}^{({\lambda })}}$
which are enumerated to be below some
![]() $\beta _m, m \leq n$
in less than n steps.
$\beta _m, m \leq n$
in less than n steps.
Note that, if
![]() $\lvert \sigma \rvert < l_1$
then
$\lvert \sigma \rvert < l_1$
then
![]() $\sigma $
is trivially in
$\sigma $
is trivially in
![]() $\tilde {T}_\lambda $
and since if
$\tilde {T}_\lambda $
and since if
![]() ${\beta }^{\Diamond } = \lambda $
and
${\beta }^{\Diamond } = \lambda $
and
![]() $l^{\Diamond }(\beta )> l^{\Diamond }(\beta _m)$
then
$l^{\Diamond }(\beta )> l^{\Diamond }(\beta _m)$
then
![]() $\beta \geq _{\mathcal {O}} \beta _m$
we verify that
$\beta \geq _{\mathcal {O}} \beta _m$
we verify that
![]() $ \tilde {T}_\lambda $
satisfies the uniform computation demands. It remains only to verify that
$ \tilde {T}_\lambda $
satisfies the uniform computation demands. It remains only to verify that
![]() $[ \tilde {T}_\lambda ] = [T_\lambda ]$
. Clearly,
$[ \tilde {T}_\lambda ] = [T_\lambda ]$
. Clearly,
![]() $[\tilde {T}_\lambda ] \supset [T_\lambda ]$
since
$[\tilde {T}_\lambda ] \supset [T_\lambda ]$
since
![]() $T_\lambda \subset \tilde {T}_\lambda $
. Now suppose that
$T_\lambda \subset \tilde {T}_\lambda $
. Now suppose that
![]() $f \notin [T_\lambda ]$
and let
$f \notin [T_\lambda ]$
and let
![]() $\sigma \prec f$
such that
$\sigma \prec f$
such that
![]() $\sigma \notin T_\lambda $
. Some finite computation from
$\sigma \notin T_\lambda $
. Some finite computation from
![]() ${{X}^{({\lambda })}}$
places
${{X}^{({\lambda })}}$
places
![]() $\sigma \notin T_\lambda $
in s stages. Since
$\sigma \notin T_\lambda $
in s stages. Since
![]() ${{X}^{({\lambda })}} = \oplus _{n \in \omega } {{X}^{({{\left \{ \lambda \right \}}^{\mathcal {O}}(n)})}}$
there is some n such that the use of this computation only mentions notations below
${{X}^{({\lambda })}} = \oplus _{n \in \omega } {{X}^{({{\left \{ \lambda \right \}}^{\mathcal {O}}(n)})}}$
there is some n such that the use of this computation only mentions notations below
![]() $\beta _n$
. Let
$\beta _n$
. Let
![]() $t \geq s$
be a stage where every notation mentioned in the use of this computation has been enumerated to be below
$t \geq s$
be a stage where every notation mentioned in the use of this computation has been enumerated to be below
![]() $\beta _n$
. Now if
$\beta _n$
. Now if
![]() $\lvert \tau \rvert = l_{t+1}, \tau \succ \sigma $
then
$\lvert \tau \rvert = l_{t+1}, \tau \succ \sigma $
then
![]() $\tau \notin T_\lambda $
.
$\tau \notin T_\lambda $
.
Finally, we note that not only is the limit lemma completely uniform and relativizable we can ensure that when we iterate its application only the final limit is at risk of being undefined.
Lemma B.7. Given a functional
![]() $\Upsilon _2$
, we can uniformly construct a computable functional
$\Upsilon _2$
, we can uniformly construct a computable functional
![]() $\rho ^{X}(z, s_1, s_0)$
such that if
$\rho ^{X}(z, s_1, s_0)$
such that if
![]() $\rho ^{X}_{1}(z, s_1) \overset {{\tiny def}}{=} \lim _{s_0 \to \infty } \rho ^{X}_n(z, s_1, s_0)$
then:
$\rho ^{X}_{1}(z, s_1) \overset {{\tiny def}}{=} \lim _{s_0 \to \infty } \rho ^{X}_n(z, s_1, s_0)$
then:
-
• For all X
 $\rho ^{X}_1, \rho ^{X}$
are total binary valued functions.
$\rho ^{X}_1, \rho ^{X}$
are total binary valued functions. -
•
 $\Upsilon _2({X}^{\prime \prime };z)\downarrow \in {\left \{0,1\right \}}$
iff
$\Upsilon _2({X}^{\prime \prime };z)\downarrow \in {\left \{0,1\right \}}$
iff
 $\rho _2^{X}(z)\downarrow = \Upsilon _2({X}^{\prime \prime };z)$
.
$\rho _2^{X}(z)\downarrow = \Upsilon _2({X}^{\prime \prime };z)$
.
Moreover,
![]() $\rho ^{X}(z,s_1,s_0)$
depends only on the computations of the form
$\rho ^{X}(z,s_1,s_0)$
depends only on the computations of the form
![]() $\Upsilon _2(\tau ;z)$
for some
$\Upsilon _2(\tau ;z)$
for some
![]() $\tau $
.
$\tau $
.
Proof Using the limit lemma relativized to
![]() ${X}^{\prime }$
we can derive a total computable binary valued functional whose limit gives
${X}^{\prime }$
we can derive a total computable binary valued functional whose limit gives
![]() $\Upsilon _2({X}^{\prime \prime };z)$
when
$\Upsilon _2({X}^{\prime \prime };z)$
when
![]() $\Upsilon _2({X}^{\prime \prime };z)\downarrow \in {\left \{0,1\right \}}$
and, by alternating between
$\Upsilon _2({X}^{\prime \prime };z)\downarrow \in {\left \{0,1\right \}}$
and, by alternating between
![]() $0,1$
whenever we haven’t settled on a computation witnessing
$0,1$
whenever we haven’t settled on a computation witnessing
![]() $\Upsilon _2({X}^{\prime \prime };z)\downarrow \in {\left \{0,1\right \}}$
, ensures that otherwise the limit fails to exist. Using a stagewise approximation to
$\Upsilon _2({X}^{\prime \prime };z)\downarrow \in {\left \{0,1\right \}}$
, ensures that otherwise the limit fails to exist. Using a stagewise approximation to
![]() $ {X}^{\prime }$
gives us our functional
$ {X}^{\prime }$
gives us our functional
![]() $\rho ^{X}$
and ensures
$\rho ^{X}$
and ensures
![]() $\rho ^{X}_1$
is total. The moreover claim follows by attending to the details of the relativization of the limit lemma to
$\rho ^{X}_1$
is total. The moreover claim follows by attending to the details of the relativization of the limit lemma to
![]() ${X}^{\prime }$
.
${X}^{\prime }$
.