Article contents
PROFINITENESS IN FINITELY GENERATED VARIETIES IS UNDECIDABLE
Published online by Cambridge University Press: 21 December 2018
Abstract
Profinite algebras are exactly those that are isomorphic to inverse limits of finite algebras. Such algebras are naturally equipped with Boolean topologies. A variety  ${\cal V}$ is standard if every Boolean topological algebra with the algebraic reduct in
${\cal V}$ is standard if every Boolean topological algebra with the algebraic reduct in  ${\cal V}$ is profinite.
${\cal V}$ is profinite.
We show that there is no algorithm which takes as input a finite algebra A of a finite type and decide whether the variety 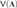 $V\left( {\bf{A}} \right)$ generated by A is standard. We also show the undecidability of some related properties. In particular, we solve a problem posed by Clark, Davey, Freese, and Jackson.
$V\left( {\bf{A}} \right)$ generated by A is standard. We also show the undecidability of some related properties. In particular, we solve a problem posed by Clark, Davey, Freese, and Jackson.
We accomplish this by combining two results. The first one is Moore’s theorem saying that there is no algorithm which takes as input a finite algebra A of a finite type and decides whether 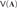 $V\left( {\bf{A}} \right)$ has definable principal subcongruences. The second is our result saying that possessing definable principal subcongruences yields possessing finitely determined syntactic congruences for varieties. The latter property is known to yield standardness.
$V\left( {\bf{A}} \right)$ has definable principal subcongruences. The second is our result saying that possessing definable principal subcongruences yields possessing finitely determined syntactic congruences for varieties. The latter property is known to yield standardness.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 2
- Cited by

