Article contents
Proof of the independence of the primitive symbols of Heyting's calculus of propositions
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper I shall show that no one of the four primitive symbols of Heyting's calculus of propositions is definable in terms of the other three. So as to make the paper self-contained, I begin by stating the rules and primitive sentences given by Heyting.
The primitive symbols of the calculus are “⅂”, “∨”, “∧”, and “⊃”, which may be read, respectively, as “not,” “either…or,” “and,” and “if…then.” The symbol “⊃⊂”, which may be read “if and only if,” is defined in terms of these as follows:
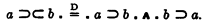
The rule of substitution is assumed, and the rule that S2 follows from S1 and S1⊃S2; in addition it is assumed that S1∧S2 follows from S1 and S2. The primitive sentences are as follows:
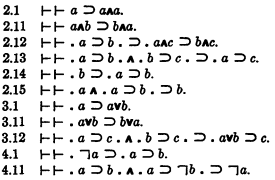
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1939
References
1 See Heyting, A., Die formalen Regeln der intuitionistischen Logik, Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 1930, pp. 42–56Google Scholar.
2 Loc: cit., page 44.
3 As a matter of fact, the formula
is satisfied by Heyting's three-element matrix.
4 It will be observed that this method of showing the independence of undefined notions is altogether different from the method of Padoa (Essai d'une théorie algébrique des nombres entiers, précédé d'une introduction logique à une théorie déductive quelconque, Bibliothèque du Congrès International de Philosophie, vol. 3 (1901), pp. 309–365Google Scholar). For Padoa's method would require two distinct realizations in order to show the independence of a given primitive, while the present method requires but one. Properly speaking, we have here, not just a difference in method, but rather a difference in the thing proved. When Padoa's method can be applied, to show the independence of a primitive operation for example, we can conclude that the values of this operation are not determined when values are assigned to the other notions. When the present method is applied, however, we can conclude merely, that the operation whose independence we are proving, cannot be expressed by means of a formula involving only free variables and the other notions.
5 The idea of forming direct products of matrices in this way is suggested by Jaśkowski, , Recherches sur le système de la logique intuitioniste, Actes du Congrès International de Philosophie Scientifique, Paris 1936, part VI, pp. 58–61Google Scholar. This author also describes an operation “Γ” which is such, that if M is an n-element matrix satisfying Heyting's postulates, then Γ(M) will be an (n + 1)-element matrix also satisfying these postulates. It will perhaps be of some interest to those familiar with Jaśkowski's paper, to remark that my Matrix II is the same as Γ(B 4), where B 4 is a four-element Boolean algebra. Also that Matrix I is the.same as Γ(B 2), where B 2 is a two-element Boolean algebra (i.e., the usual matrix for classical logic). It is of course well known that B 4 is the direct product of B 2 by itself.
- 22
- Cited by

