Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T02:55:54.862Z Has data issue: false hasContentIssue false
  • English
  • Français

Proofs of non-deducibility in intuitionistic functional calculus

Published online by Cambridge University Press:  12 March 2014

Andkzej Mostowski
Andkzej Mostowski*
Affiliation:
University of Warsaw
Get access Rights & Permissions [Opens in a new window]

Extract

It has been proved by S. C. Kleene and David Nelson that the formula

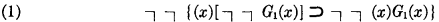
is intuitionistically non-deducible, i.e., non-deducible within the intuitionistic functional calculus.

The aim of this note is to outline a general method which permits us to establish the intuitionistic non-deducibility of many formulas and in particular of the formula (1).

Type
Articles
Information
The Journal of Symbolic Logic , Volume 13 , Issue 4 , December 1948 , pp. 204 - 207
Copyright
Copyright © Association for Symbolic Logic 1948

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Kleene, S. C., On the interpretation of intuitionistic number theory, this Journal, vol. 10 (1945), pp. 109–124Google Scholar; see especially the last sentence of §10, p. 117.

2 Birkhoff, Garrett, Lattice theory, New York 1940CrossRefGoogle Scholar. See also McKinsey, J. C. C. and Tarski, A., On closed elements in closure algebras, Annals of mathematics, vol. 47 (1946), pp. 122–162.CrossRefGoogle Scholar

3 See Birkhoff, loc. cit. p. 128, and McKinsey and Tarski, loc. cit., Theorem 1.3.