Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kahle, Reinhard
2001.
Truth in Applicative Theories.
Studia Logica,
Vol. 68,
Issue. 1,
p.
103.
Jäger, Gerhard
Kahle, Reinhard
and
Studer, Thomas
2001.
Universes in explicit mathematics.
Annals of Pure and Applied Logic,
Vol. 109,
Issue. 3,
p.
141.
Kahle, Reinhard
2002.
Mathematical Proof Theory in the Light of Ordinal Analysis.
Synthese,
Vol. 133,
Issue. 1-2,
p.
237.
Rüede, Christian
and
Strahm, Thomas
2002.
Intuitionistic Fixed Point Theories for Strictly Positive Operators.
MLQ,
Vol. 48,
Issue. 2,
p.
195.
Kahle, Reinhard
2003.
Universes over Frege structures.
Annals of Pure and Applied Logic,
Vol. 119,
Issue. 1-3,
p.
191.
Rüede, Christian
2003.
The proof-theoretic analysis of Σ11 transfinite dependent choice.
Annals of Pure and Applied Logic,
Vol. 122,
Issue. 1-3,
p.
195.
Jäger, Gerhard
2004.
An intensional fixed point theory over first order arithmetic.
Annals of Pure and Applied Logic,
Vol. 128,
Issue. 1-3,
p.
197.
Jäger, Gerhard
and
Strahm, Thomas
2005.
Reflections on reflections in explicit mathematics.
Annals of Pure and Applied Logic,
Vol. 136,
Issue. 1-2,
p.
116.
Probst, Dieter
2005.
On the relationship between fixed points and iteration in admissible set theory without foundation.
Archive for Mathematical Logic,
Vol. 44,
Issue. 5,
p.
561.
Andrea, Cantini
2009.
Logic from Russell to Church.
Vol. 5,
Issue. ,
p.
875.
Fujimoto, Kentaro
2012.
Classes and truths in set theory.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 11,
p.
1484.
Ranzi, Florian
and
Strahm, Thomas
2014.
A note on the theory SID<ω of stratified induction.
Mathematical Logic Quarterly,
Vol. 60,
Issue. 6,
p.
487.
Kahle, Reinhard
2015.
Unifying the Philosophy of Truth.
Vol. 36,
Issue. ,
p.
143.
Glanzberg, Michael
2015.
Unifying the Philosophy of Truth.
Vol. 36,
Issue. ,
p.
211.
Jäger, Gerhard
and
Probst, Dieter
2015.
Gentzen's Centenary.
p.
425.
Schurz, Christine
2015.
Contextual-Hierarchical Reconstructions of the Strengthened Liar Problem.
Journal of Philosophical Logic,
Vol. 44,
Issue. 5,
p.
517.
Cantini, Andrea
2016.
Advances in Proof Theory.
Vol. 28,
Issue. ,
p.
31.
Cantini, Andrea
Fujimoto, Kentaro
and
Halbach, Volker
2017.
Feferman on Foundations.
Vol. 13,
Issue. ,
p.
287.
Jäger, Gerhard
2017.
Logic Colloquium 2000.
p.
272.
Ranzi, Florian
and
Strahm, Thomas
2019.
A flexible type system for the small Veblen ordinal.
Archive for Mathematical Logic,
Vol. 58,
Issue. 5-6,
p.
711.

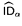 and
and 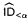 ; the exact proof-theoretic ordinals of these systems are presented.
; the exact proof-theoretic ordinals of these systems are presented.