Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rosenberg, Richard
1982.
Recursively Enumerable Images of Arithmetic Sets.
Mathematical Logic Quarterly,
Vol. 28,
Issue. 14-18,
p.
189.

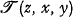 which binumerates the Kleene
which binumerates the Kleene 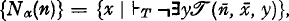 and which has the additional property that {
and which has the additional property that {