Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T17:33:22.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramsey cardinals, α-Erdös cardinals, and the core model

Published online by Cambridge University Press:  12 March 2014

Dirk R. H. Schlingmann
Dirk R. H. Schlingmann*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, Michigan 48109-1092
Get access Rights & Permissions [Opens in a new window]

Extract

The core model K was introduced by R. B. Jensen and A. J. Dodd [DoJ]. K is the union of Gödel's constructible universe L together with all mice, i.e., 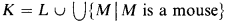, and K is a transitive model of ZFC + (V = K) + GCH (see [DoJ]). V = K is consistent with the existence of Ramsey cardinals [M], and if cf(α) > ω, V = K is consistent with the existence of α-Erdös cardinals [J]. Let K be Ramsey. Then there is a smallest inner model Wκ of ZFC in which κ is Ramsey. We have Wκ ⊨ V = K and Wκ ⊆ K [M]. The existence of Wκ with 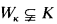is equivalent to the existence of a sharplike mouse 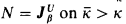on N ⊨ K with N ⊨ κ Ramsey. (A mouse N on 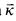is called sharplike provided 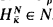.) We have 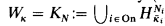, where 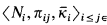is the mouse iteration of N. N is the oleast mouse not in Wκ (see [J] and [DJKo]). Here < denotes the mouse order. The context always clarifies whether the mouse order or the usual <-relation is meant.

The main result of §1 is that Wκ ⊨ κ is the only Ramsey cardinal. A similar result has been found true in the smallest inner model L[U] of ZFC + “κ is measurable” if U is a normal measure on κ: L[U] ⊨ κ is the only measurable cardinal [Ku].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 1 , March 1991 , pp. 108 - 114
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Do]Dodd, A. J., The core model, London Mathematical Society Lecture Note Series, vol. 61, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[DoJ]Dodd, A. J. and Jensen, R. B., The core model, Annals of Mathematical Logic, vol. 20 (1981), pp. 43–75.CrossRefGoogle Scholar
[DJKo]Donder, H.-D., Jensen, R. B., and Koppelberg, B. J., Some applications of the core model, Preprint No. 115, Free University of Berlin, Berlin, 1981; published as Set theory and model theory (Bonn, 1977), Lecture Notes in Mathematics, vol. 872, Springer-Verlag, Berlin, 1981, pp. 55–97.CrossRefGoogle Scholar
[J]Jensen, R. B., Applications of K, Handwritten notes, Bonn, 1977.Google Scholar
[Ku]Kunen, K., Some applications of iterated ultrapowers in set theory, Annals of Mathematical Logic, vol. 1 (1970), pp. 179–227.CrossRefGoogle Scholar
[M]Mitchell, W., Ramsey cardinals and constructibility, this Journal, vol. 44 (1979), pp. 260–266.Google Scholar
[S]Schlingmann, D. R. H., Partition cardinals and the core model, Dissertation, Free University of Berlin, Berlin, 1988.Google Scholar