Article contents
Random reals, the rainbow Ramsey theorem, and arithmetic conservation
Published online by Cambridge University Press: 12 March 2014
Abstract
We investigate the question “To what extent can random reals be used as a tool to establish number theoretic facts?” Let 2-RAN be the principle that for every real X there is a real R which is 2-random relative to X. In Section 2, we observe that the arguments of Csima and Mileti [3] can be implemented in the base theory RCA0 and so RCA0 + 2-RAN implies the Rainbow Ramsey Theorem. In Section 3, we show that the Rainbow Ramsey Theorem is not conservative over RCA0 for arithmetic sentences. Thus, from the Csima–Mileti fact that the existence of random reals has infinitary-combinatorial consequences we can conclude that 2-RAN has non-trivial arithmetic consequences. In Section 4, we show that 2-RAN is conservative over RCA0 + BΣ2 for 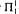 -sentences. Thus, the set of first-order consequences of 2-RAN is strictly stronger than P− + IΣ1 and no stronger than P− + BΣ2.
-sentences. Thus, the set of first-order consequences of 2-RAN is strictly stronger than P− + IΣ1 and no stronger than P− + BΣ2.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2013
References
REFERENCES
- 6
- Cited by

