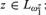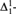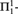Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bienvenu, Laurent
Greenberg, Noam
and
Monin, Benoit
2017.
Continuous higher randomness.
Journal of Mathematical Logic,
Vol. 17,
Issue. 01,
p.
1750004.
Monin, Benoit
2017.
Higher Randomness and Forcing with Closed Sets.
Theory of Computing Systems,
Vol. 60,
Issue. 3,
p.
421.
GREENBERG, NOAM
and
MONIN, BENOIT
2017.
HIGHER RANDOMNESS AND GENERICITY.
Forum of Mathematics, Sigma,
Vol. 5,
Issue. ,
Bienvenu, Laurent
Greenberg, Noam
and
Monin, Benoit
2021.
Bad oracles in higher computability and randomness.
Israel Journal of Mathematics,
Vol. 241,
Issue. 1,
p.
229.
PAULY, ARNO
WESTRICK, LINDA
and
YU, LIANG
2022.
LUZIN’S (N) AND RANDOMNESS REFLECTION.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 2,
p.
802.