Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T02:55:59.379Z Has data issue: false hasContentIssue false
  • English
  • Français

RANDOMNESS VIA INFINITE COMPUTATION AND EFFECTIVE DESCRIPTIVE SET THEORY

Published online by Cambridge University Press:  01 August 2018

MERLIN CARL  and
PHILIPP SCHLICHT
MERLIN CARL
Affiliation:
FACHBEREICH MATHEMATIK UND STATISTIK UNIVERSITÄT KONSTANZ 78457 KONSTANZ, GERMANYE-mail:merlin.carl@uni-konstanz.de
PHILIPP SCHLICHT
Affiliation:
MATHEMATISCHES INSTITUT, UNIVERSITÄT BONN ENDENICHER ALLEE 60 53115 BONN, GERMANYE-mail:schlicht@math.uni-bonn.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We study randomness beyond 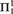${\rm{\Pi }}_1^1$-randomness and its Martin-Löf type variant, which was introduced in [16] and further studied in [3]. Here we focus on a class strictly between 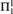${\rm{\Pi }}_1^1$ and 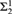${\rm{\Sigma }}_2^1$ that is given by the infinite time Turing machines (ITTMs) introduced by Hamkins and Kidder. The main results show that the randomness notions associated with this class have several desirable properties, which resemble those of classical random notions such as Martin-Löf randomness and randomness notions defined via effective descriptive set theory such as 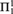${\rm{\Pi }}_1^1$-randomness. For instance, mutual randoms do not share information and a version of van Lambalgen’s theorem holds.

Towards these results, we prove the following analogue to a theorem of Sacks. If a real is infinite time Turing computable relative to all reals in some given set of reals with positive Lebesgue measure, then it is already infinite time Turing computable. As a technical tool towards this result, we prove facts of independent interest about random forcing over increasing unions of admissible sets, which allow efficient proofs of some classical results about hyperarithmetic sets.

Keywords

03D6003D3203E15algorithmic randomnessinfinite time Turing machineseffective descriptive set theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 766 - 789
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andretta, A. and Camerlo, R., The descriptive set theory of the Lebesgue density theorem. Advances in Mathematics, vol. 234 (2013), pp. 1–42.CrossRefGoogle Scholar
Barwise, J., Admissible Sets and Structures, Perspectives in Mathematical Logic, Springer-Verlag, Berlin-New York, 1975.CrossRefGoogle Scholar
Bienvenu, L., Greenberg, N., and Monin, B., Continuous higher randomness. Journal of Mathematical Logic, vol. 17 (2017), no. 1, pp. 1750004, 53.CrossRefGoogle Scholar
Bartoszyński, T. and Judah, H., Set Theory. On the Structure of the Real Line, A K Peters Ltd., Wellesley, MA, 1995.Google Scholar
Carl, M., Randomness and degree theory for infinite time register machines. Computability, vol. 5 (2016), no. 2, pp. 181–196.CrossRefGoogle Scholar
Carl, M., Infinite time recognizability from generic oracles and the recognizable jump operator. Computability, vol. 6 (2017), no. 3, pp. 223–247.CrossRefGoogle Scholar
Carl, M., Fischbach, T., Koepke, P., Miller, R., Nasfi, M., and Weckbecker, G., The basic theory of infinite time register machines. Archive for Mathematical Logic, vol. 49 (2010), no. 2, pp. 249–273.CrossRefGoogle Scholar
Carl, M. and Schlicht, P., Infinite computations with random oracles. Notre Dame Journal of Formal Logic, vol. 58 (2017), no. 2, pp. 249–270.CrossRefGoogle Scholar
Carl, M., Schlicht, P., and Welch, P. D., Recognizable sets and Woodin cardinals: computation beyond the constructible universe. Annals of Pure and Applied Logic, to appear.Google Scholar
Chong, C. T. and Yu, L., Randomness in the higher setting, this Journal, vol. 80 (2015), no. 4, pp. 1131–1148.Google Scholar
Chong, C. T. and Yu, L.., Recursion Theory, De Gruyter Series in Logic and its Applications, vol. 8, De Gruyter, Berlin, 2015.CrossRefGoogle Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Friedman, S.-D. and Welch, P. D., Hypermachines, this Journal, vol. 76 (2011), no. 2, pp. 620–636.Google Scholar
Hjorth, G., Vienna notes on effective descriptive set theory and admissible sets, 2010. Available at http://www.math.uni-bonn.de/people/logic/events/young-set-theory-2010/Hjorth.pdf.Google Scholar
Hamkins, J. D. and Lewis, A., Infinite time Turing machines, this Journal, vol. 65 (2000), no. 2, pp. 567–604.Google Scholar
Hjorth, G. and Nies, A., Randomness via effective descriptive set theory. Journal of the London Mathematical Society (2), vol. 75 (2007), no. 2, pp. 495–508.CrossRefGoogle Scholar
Ikegami, D., Forcing absoluteness and regularity properties. Annals of Pure and Applied Logic, vol. 161 (2010), no. 7, pp. 879–894.CrossRefGoogle Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Kanamori, A., The Higher Infinite, second ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2009.Google Scholar
Kechris, A. S., Measure and category in effective descriptive set theory. Annals of Mathematical Logic, vol. 5 (1972/73), pp. 337–384.Google Scholar
Koepke, P., Infinite Time Register Machines, Springer, Berlin, Heidelberg, 2006, pp. 257–266.Google Scholar
Monin, B., Higher randomness and forcing with closed sets, 31st International Symposium on Theoretical Aspects of Computer Science (Mayr, E. W. and Portier, N., editors), Leibniz International Proceedings in Informatics, vol. 25, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Wadern, 2014, pp. 566–577.Google Scholar
Nies, A., Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
Sacks, G. E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
Schlicht, P. and Seyfferth, B., Tree representations via ordinal machines. Computability, vol. 1 (2012), no. 1, pp. 45–57.Google Scholar
Welch, P. D., The length of infinite time Turing machine computations. Bulletin of the London Mathematical Society, vol. 32 (2000), no. 2, pp. 129–136.CrossRefGoogle Scholar
Welch, P. D.., Post’s and other problems in higher type supertasks, Classical and New Paradigms of Computation and their Complexity Hierarchies (Räsch, T., Löwe, B., and Piwinger, B., editors), Trends in Logic, vol. 23, Kluwer Academic Publishers, Dordrecht, 2004, pp. 223–237.CrossRefGoogle Scholar
Welch, P. D.., Characteristics of discrete transfinite time Turing machine models: Halting times, stabilization times, and normal form theorems. Theoretical Computer Science, vol. 410 (2009), no. 4–5, pp. 426–442.CrossRefGoogle Scholar
Yu, L., Descriptive set theoretical complexity of randomness notions. Fundamenta Mathematicae, vol. 215 (2011), no. 3, pp. 219–231.CrossRefGoogle Scholar
Yu, L. and Zhu, Y., On the reals which cannot be random, Computability and Complexity (Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Lecture Notes in Computer Science, vol. 10010, Springer, Cham, 2017, pp. 611–622.CrossRefGoogle Scholar