Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T07:51:16.615Z Has data issue: false hasContentIssue false
  • English
  • Français

RANK LOGIC IS DEAD, LONG LIVE RANK LOGIC!

Published online by Cambridge University Press:  14 March 2019

ERICH GRÄDEL  and
WIED PAKUSA
ERICH GRÄDEL
Affiliation:
MATHEMATICAL FOUNDATIONS OF COMPUTER SCIENCE RWTH AACHEN UNIVERSITY D-52056 AACHEN, GERMANYE-mail: graedel@logic.rwth-aachen.de
WIED PAKUSA
Affiliation:
MATHEMATICAL FOUNDATIONS OF COMPUTER SCIENCE RWTH AACHEN UNIVERSITY D-52056 AACHEN, GERMANYE-mail: pakusa@logic.rwth-aachen.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the search for a logic for polynomial time, we study rank logic (FPR) which extends fixed-point logic with counting (FPC) by operators that determine the rank of matrices over finite fields. While FPR can express most of the known queries that separate FPC from Ptime, almost nothing was known about the limitations of its expressive power.

In our first main result we show that the extensions of FPC by rank operators over different prime fields are incomparable. This solves an open question posed by Dawar and Holm and also implies that rank logic, in its original definition with a distinct rank operator for every field, fails to capture polynomial time. In particular we show that the variant of rank logic 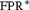${\text{FPR}}^{\text{*}}$ with an operator that uniformly expresses the matrix rank over finite fields is more expressive than FPR.

One important step in our proof is to consider solvability logic FPS which is the analogous extension of FPC by quantifiers which express the solvability problem for linear equation systems over finite fields. Solvability logic can easily be embedded into rank logic, but it is open whether it is a strict fragment. In our second main result we give a partial answer to this question: in the absence of counting, rank operators are strictly more expressive than solvability quantifiers.

Keywords

68Q1903C13finite model theorydescriptive complexitylogiclinear algebra
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 54 - 87
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abu Zaid, F., Grädel, E., Grohe, M., and Pakusa, W., Choiceless polynomial time on structures with small Abelian colour classes, Mathematical Foundations of Computer Science 2014 (Csuhaj-Varjù, E., Dietzfelbinger, M., and Ésik, Z., editors), Lecture Notes in Computer Science, vol. 8634, Springer, Berlin, 2014, pp. 50–62.Google Scholar
Atserias, A., Bulatov, A., and Dawar, A., Affine systems of equations and counting infinitary logic. Theoretical Computer Science, vol. 410 (2009), pp. 1666–1683.10.1016/j.tcs.2008.12.049CrossRefGoogle Scholar
Buntrock, G., Hertrampf, U., Damm, C., and Meinel, C., Structure and importance of logspace-mod-classes, Symposium on Theoretical Aspects of Computer Science ’91 (Choffrut, C. and Jantzen, M., editors), Springer, Berlin, 1991, pp. 360–371.Google Scholar
Cai, J., Fürer, M., and Immerman, N., An optimal lower bound on the number of variables for graph identification. Combinatorica, vol. 12 (1992), no. 4, pp. 389–410.10.1007/BF01305232CrossRefGoogle Scholar
Dawar, A., The nature and power of fixed-point logic with counting. SIGLOG News, vol. 2 (2015), pp. 8–21.Google Scholar
Dawar, A., Grädel, E., Holm, B., Kopczynski, E., and Pakusa, W., Definability of linear equation systems over groups and rings. Logical Methods in Computer Science, vol. 9 (2013), no. 4.10.2168/LMCS-9(4:12)2013CrossRefGoogle Scholar
Dawar, A., Grohe, M., Holm, B., and Laubner, B., Logics with rank operators, Proceedings of the 24th Annual Symposium on Logic in Computer Science, LICS 2009, IEEE Computer Society, Washington, DC, 2009, pp. 113–122.10.1109/LICS.2009.24CrossRefGoogle Scholar
Dawar, A. and Holm, B., Pebble games with algebraic rules, Automata, Languages, and Programming-ICALP 2012 (Czumaj, A., Mehlhorn, K., Pitts, A., and Wattenhofer, R., editors), Springer, Berlin, 2012, pp. 251–262.Google Scholar
Ebbinghaus, H.-D. and Flum, J., Finite Model Theory, second ed., Springer-Verlag, Berlin, 1999.Google Scholar
Grädel, E., Kolaitis, P., Libkin, L., Marx, M., Spencer, J., Vardi, M, Venema, Y., and Weinstein, S., Finite Model Theory and Its Applications, Springer, 2007.Google Scholar
Grohe, M., The quest for a logic capturing PTIME, Proceedings of the 23rd Annual Symposium on Logic in Computer Science, LICS 2008, IEEE Computer Society, Washington, DC, 2008, pp. 267–271.10.1109/LICS.2008.11CrossRefGoogle Scholar
Gurevich, Y. and Shelah, S., On finite rigid structures, this Journal, vol. 61 (1996), no. 02, pp. 549–562.Google Scholar
Hall, M., The Theory of Groups, American Mathematical Society, Providence, RI, 1976.Google Scholar
Hertrampf, U., Reith, S., and Vollmer, H., A note on closure properties of logspace mod classes. Information Processing Letters, vol. 75 (2000), no. 3, pp. 91–93.10.1016/S0020-0190(00)00091-0CrossRefGoogle Scholar
Holm, B., Descriptive complexity of linear algebra, Ph.D. thesis, University of Cambridge, 2010.Google Scholar
Laubner, B., The structure of graphs and new logics for the characterization of polynomial time, Ph.D. thesis, Humboldt-Universität Berlin, 2011.Google Scholar
Otto, M., Bounded Variable Logics and Counting: A Study in Finite Models, Springer, Berlin, 1997.Google Scholar
Pakusa, W., Finite model theory with operators from linear algebra, Staatsexamensarbeit, RWTH Aachen University, 2010.Google Scholar
Pakusa, W., Linear equation systems and the search for a logical characterisation of polynomial time, Ph.D. thesis, RWTH Aachen University, 2016.Google Scholar
Papadimitriou, C., Computational Complexity, Addison-Wesley, Boston, 1995.Google Scholar
Torán, J., On the hardness of graph isomorphism. SIAM Journal on Computing, vol. 33 (2004), no. 5, pp. 1093–1108.10.1137/S009753970241096XCrossRefGoogle Scholar