Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T16:28:56.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Reconstruction of homogeneous relational structures

Published online by Cambridge University Press:  12 March 2014

Silvia Barbina  and
Dugald Macpherson
Silvia Barbina
Affiliation:
Departament de Lògica, Història i Filosofia de la Ciència, Universitat de Barcelona, C/ Montalegre, 6, 08001 Barcelona, Spain. E-mail: silvia.barbina@gmail.com
Dugald Macpherson
Affiliation:
Department of Pure Mathematics, University of Leedsleeds LS2 9JT. England, UK. E-mail: h.d.macpherson@leeds.ac.uk
Get access Rights & Permissions [Opens in a new window]

Extract

This paper contains a result on the reconstruction of certain homogeneous transitive ω-categorical structures from their automorphism group. The structures treated are relational. In the proof it is shown that their automorphism group contains a generic pair (in a slightly non-standard sense, coming from Baire category).

Reconstruction results give conditions under which the abstract group structure of the automorphism group Aut(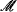) of an ω-categorical structure 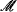determines the topology on Aut(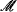), and hence determines 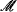up to bi-interpretability, by [1]; they can also give conditions under which the abstract group Aut(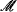) determines the permutation group ⟨Aut (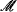), 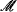⟩. so determines 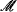up to bi-definability. One such condition has been identified by M. Rubin in [12], and it is related to the definability, in Aut(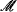), of point stabilisers. If the condition holds, the structure is said to have a weak ∀∃ interpretation, and Aut(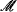) determines 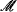up to bi-interpretability or, in some cases, up to bi-definability.

A better-known approach to reconstruction is via the ‘small index property’: an ω-categorical stucture 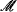has the small index property if any subgroup of Aut(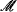) of index less than 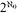is open. This guarantees that the abstract group structure of Aut(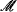) determines the topology, so if 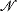is ω-categorical with Aut(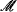) ≅ Aut(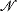) then 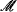and 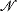are bi-interpretable.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 3 , September 2007 , pp. 792 - 802
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ahlbrandt, G. and Ziegler, M., Quasi-finitely axiomatisable totally categorical theories, Annals of Pure and Applied Logic, vol. 30 (1986), pp. 63–82, Stability in model theory (Trento, 1984).CrossRefGoogle Scholar
[2] Barbina, S., Automorphism groups of omega-categorical structures, Ph.D. thesis, University of Leeds, 2004.Google Scholar
[3] Barbina, S., Reconstruction of classical geometries from their automorphism groups, Journal of the London Mathematical Society, to appear.Google Scholar
[4] Evans, D., Examples of ℵ0-categorical structures, Automorphisms of first order structures (Kaye, R. and Macpherson, D., editors), Cambridge University Press, 1994, pp. 33–72.Google Scholar
[5] Henson, C. W., Countable homogeneous relational structures and ℵ0-categorical theories, this Journal, vol. 37 (1972), pp. 494–500.Google Scholar
[6] Herwig, B., Extending partial isomorphisms of finite structures, Combinatorica, vol. 15 (1995), no. 3, pp. 365–371.CrossRefGoogle Scholar
[7] Herwig, B., Extending partial isomorphisms for the small index property of many ω-categorical structures, Israel Journal of Mathematics, vol. 107 (1998), pp. 93–123.CrossRefGoogle Scholar
[8] Hodges, W. A., Hodkinson, I. M., Lascar, D., and Shelah, S., The small index property for ω-stable ω-categorical structures and for the random graph, Journal of the London Mathematical Society, vol. 48 (1993), no. 2, pp. 204–218.Google Scholar
[9] Hodkinson, I. M. and Otto, M., Finite conformal hypergraph covers and Gaifman cliques infinite structures, The Bulletin of Symbolic Logic, vol. 9 (2003), no. 3, pp. 387–405.CrossRefGoogle Scholar
[10] Hrushovski, E., Extending partial automorphisms, Combinatorica, vol. 12 (1992), no. 4, pp. 411–416.CrossRefGoogle Scholar
[11] Kechris, A., Classical descriptive set theory, Springer, New York, 1994.Google Scholar
[12] Rubin, M., On the reconstruction of ℵ0-categorical structures from their autmorphism groups, Proceedings of the London Mathematical Society, vol. 69 (1992), no. 3, pp. 225–249.Google Scholar