Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-31T05:29:57.739Z Has data issue: false hasContentIssue false
  • English
  • Français

Relation algebra reducts of cylindric algebras and complete representations

Published online by Cambridge University Press:  12 March 2014

Robin Hirsch
Robin Hirsch*
Affiliation:
Department of Computer Science, University College, Gower Street, London WC1E 6BT, United Kingdom, E-mail: R.Hirsch@cs.ucl.ac.uk, URL: http://www.cs.ucl.ac.Uk/staff/R.Hirsch
Get access Rights & Permissions [Opens in a new window]

Abstract

We show, for any ordinal γ ≥ 3, that the class ℜaCAγ is pseudo-elementary and has a recursively enumerable elementary theory. ScK denotes the class of strong subalgebras of members of the class K. We devise games, Fn (3 ≤ n ≤ ω), G, H, and show, for an atomic relation algebra 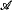with countably many atoms, that

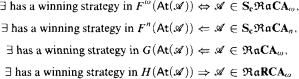
for 3 ≤ n < ω. We use these games to show, for γ > 5 and any class K of relation algebras satisfying

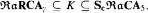
that K is not closed under subalgebras and is not elementary. For infinite γ, the inclusion ℜaCAγ ⊂ ScℜaCAγ is strict.

For infinite γ and for a countable relation algebra 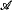we show that 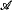has a complete representation if and only if 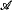is atomic and ∃ has a winning strategy in F (At(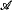)) if and only if 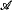is atomic and 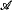∈ ScℜaCAγ.

Keywords

relation algebracylindric algebracomplete representation

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 2 , June 2007 , pp. 673 - 703
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Andréka, H., Düntsch, I., and Németi, I., A nonpermulational integral relation algebra, Michigan Mathematics Journal, vol. 39 (1992), pp. 371–384.CrossRefGoogle Scholar
[2]Andréka, H., Monk, J., and Németi, I. (editors), Algebraic logic, Colloquia Mathematica Societatis Janos Bolyai, vol. 54, North-Holland, 1991.Google Scholar
[3]Anellis, I. And Houser, N., Nineteenth century roots of algebraic logic and universal algebra, In Andréka et al. [2], pp. 1–36.Google Scholar
[4]Henkin, L., Monk, J., and Tarski, A., Cylindric algebras part I, North-Holland, 1971.Google Scholar
[5]Henkin, L., Monk, J., and Tarski, A., Cylindric algebras part II, North-Holland, 1985.Google Scholar
[6]Hirsch, R. and Hodkinson, I., Relation algebras by games, Elsevier Science, North-Holland, 2002.Google Scholar
[7]Maddux, R., Topics in relation algebra, Ph.D. thesis, University of California, Berkeley, 1978.Google Scholar
[8]Maddux, R., A relation algebra which is not a cylindric reduct, Algebra Universalis, vol. 27 (1990), pp. 279–288.CrossRefGoogle Scholar
[9]Maddux, R., Introductory course on relation algebras, finite-dimensional cylindric algebras, and their interconnections. In Andréka et al. [2], pp. 361–392.Google Scholar
[10]Maddux, R., The origin of relation algebras in the development and axiomatization of the calculus of relations, Studia Logica, vol. 3/4 (1991), pp. 421–455.Google Scholar
[11]Maddux, R., Pair-dense relation algebras, Transactions of the American Mathematical Society, vol. 328 (1991), no. 1, pp. 83–131.CrossRefGoogle Scholar
[12]Monk, J., Studies in cylindric algebra, Ph.D. thesis, University of California, Berkeley, 1961.Google Scholar
[13]Németi, I., The class of neat reducts is not a variety but is closed w.r.t. HP, Notre Dame Journal of Formal Logic, vol. 24 (1983), pp. 399–409.CrossRefGoogle Scholar
[14]Németi, I., Free algebras and decidability in algebraic logic, Doctor of Science dissertation, Hungarian Academy of Sciences, 1986.Google Scholar
[15]Németi, I. and Simon, A., Relation algebras from cylindric and polyadic algebras, Logic Journal of the IGPL, vol. 5 (1997), pp. 575–588.CrossRefGoogle Scholar
[16]Ahmed, T. Sayed, The class of neat reducts is not elementary, Logic Journal of the IGPL, vol. 9 (2001), pp. 625–660.Google Scholar
[17]Ahmed, T. Sayed, Martin's axiom, omitting types, and complete representations in algebraic logic, Studia Logica, vol. 72 (2002), no. 2, pp. 285–309.CrossRefGoogle Scholar
[18]Ahmed, T. Sayed and Németi, I., On neat reducts of algebras of logics, Studia Logica, vol. 68 (2001), no. 2, pp. 229–262.CrossRefGoogle Scholar
[19]Simon, A., Nonrepresentable algebras of relations, Ph.D. thesis, Mathematics Institute of the Hungarian Academy of Sciences, Budapest, 1997, http://www.renyi.hu/pub/algebraic-logic/simthes.html.Google Scholar