Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T07:09:12.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative lawlessness in intuitionistic analysis

Published online by Cambridge University Press:  12 March 2014

Joan Rand Moschovakis
Joan Rand Moschovakis*
Affiliation:
Department of Mathematics, Occidental College, Los Angeles, California 90041
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper introduces, as an alternative to the (absolutely) lawless sequences of Kreisel and Troelstra, a notion of choice sequence lawless with respect to a given class 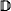of lawlike sequences. For countable 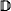, the class of 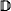-lawless sequences is comeager in the sense of Baire. If a particular well-ordered class of sequences, generated by iterating definability over the continuum, is countable then the -lawless sequences satisfy the axiom of open data and the continuity principle for functions from lawless to lawlike sequences, but fail to satisfy Troelstra's extension principle. Classical reasoning is used.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 1 , March 1987 , pp. 68 - 88
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

I wish to thank Occidental College for granting me a sabbatical leave, and UCLA for allowing me to use its research facilities, in 1983-84 when most of this work was done. I also appreciate the referee's helpful suggestions on exposition.

References

REFERENCES

Brouwer, L. E. J. [1907], Over de grondslagen der wiskunde, Ph.D. Thesis, Amsterdam; reprinted in [1975, pp. 11–101].Google Scholar
Brouwer, L. E. J. [1918], Begründung der Mengenlehre unabhängig vom logischen Satz vom ausgeschlossenen Dritten. Erster Teil: Allgemeine Mengenlehre, Verhandelingen der Koninklgke Akademie van Wetenschappen te Amsterdam, Eerste Sectie, vol. 12, no. 5; reprinted in [1975, pp. 150–190].Google Scholar
Brouwer, L. E. J. [1924], Beweis, dass jede volle Funktion gleichmässig stetig ist, Koninklgke Akademie van Wetenschappen te Amsterdam, Proceedings of the Section of Sciences, vol. 27, pp. 189–193; reprinted in [1975, pp. 286–290].Google Scholar
Brouwer, L. E. J. [1952/1953], Historical background, principles and methods of intuitionism, South African Journal of Science, vol. 49, pp. 139–146; reprinted in [1975, pp. 508–515].Google Scholar
Brouwer, L. E. J. [1975], Collected works (Heyting, A., editor). Vol. 1, North-Holland, Amsterdam.Google Scholar
Brouwer, L. E. J. [1981], Brouwer's Cambridge lectures on intuitionism (van Dalen, D., editor), Cambridge University Press, Cambridge.Google Scholar
Kleene, S. C. [1967], Constructive functions in “The foundations of intuitionistic mathematics”, Logic, methodology and philosophy of science. III ( proceedings, Amsterdam, 1967 ; van Rootselaar, B. and Staal, J. F., editors), North-Holland, Amsterdam, 1968, pp. 137–144.Google Scholar
Kleene, S. C. and Vesley, R. E., The foundations of intuitionistic mathematics, especially in relation to recursive functions, North-Holland, Amsterdam.Google Scholar
Kreisel, G. [1968]. Lawless sequences of natural numbers, Compositio Mathematica, vol. 20, pp. 222–248.Google Scholar
Kreisel, G. and Troelstra, A. S. [1970], Formal systems for some branches of intuitionistic analysis, Annals of Mathematical Logic, vol. 1, pp. 229–387.CrossRefGoogle Scholar
Lévy, Azriel [1970], Definability in axiomatic set theory. II, Mathematical logic and foundations of set theory ( proceedings, Jerusalem, 1968 ; Y. Bar-Hillel, editor), North-Holland, Amsterdam, 1970, pp. 129–145.Google Scholar
Troelstra, A. S. [1977], Choice sequences: a chapter of intuitionistic mathematics, Oxford Logic Guides, Clarendon Press, Oxford.Google Scholar
Troelstra, A. S. [1983], Analysing choice sequences, Journal of Philosophical Logic, vol. 12, pp. 197–260.CrossRefGoogle Scholar