No CrossRef data available.
Article contents
A remark on Africk's paper on Scott's interpolation theorem for Lω1ω
Published online by Cambridge University Press: 12 March 2014
Extract
In order to prove that the Scott's interpolation theorem fails in Lω1ω, H. Africk proved the following lemma in [1]. (See [1] for notations.)
Africk's Lemma. Suppose that  and
and 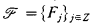 . Then every
. Then every 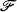 -sentence in Lω1ω is equivalent to a sentence of the form
-sentence in Lω1ω is equivalent to a sentence of the form 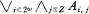 and a sentence of the form
and a sentence of the form 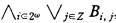 , where Ai,j, Bi,j, are Fj-sentences and there are only countable distinct Ai,j or Bi,j together.
, where Ai,j, Bi,j, are Fj-sentences and there are only countable distinct Ai,j or Bi,j together.
But this lemma is false as is shown in the following: Suppose that Z = {0,1}, Fj = {Pk,j}k⊂ω and 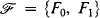 . Let A be the sentence ⋀k⊂ω(∀xPk,0(x) ∨ ∀xPk,1(x)). If Africk's Lemma is true, then there are countably many Fj-sentences
. Let A be the sentence ⋀k⊂ω(∀xPk,0(x) ∨ ∀xPk,1(x)). If Africk's Lemma is true, then there are countably many Fj-sentences 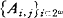 , such that A is equivalent to
, such that A is equivalent to 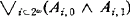 Since
Since 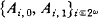 is countable, there are only countably many distinct pairs (Ai,0, Ai,1). So, we get a countable set {(Bi,0, Bi,1)}i⊂ω, such that A is equivalent to ⋁ik⊂ω(Bk,0 ∧ Bk,1). Since Bk,0 ∧ Bk,1 → ∀xPk,0(x) ∨ ∀xPk,1 is l-valid(i.e. valid in all first-order structures of cardinality 1) for every k ϵ ω, we have that either Bk,0 → ∀xPk,0(x) is 1-valid or Bk,0 → ∀xPk,1(x) is 1-valid. Let I be the set of all the k ϵ ω such that Bk,0 → ∀xPk,0(x) is 1-valid and
is countable, there are only countably many distinct pairs (Ai,0, Ai,1). So, we get a countable set {(Bi,0, Bi,1)}i⊂ω, such that A is equivalent to ⋁ik⊂ω(Bk,0 ∧ Bk,1). Since Bk,0 ∧ Bk,1 → ∀xPk,0(x) ∨ ∀xPk,1 is l-valid(i.e. valid in all first-order structures of cardinality 1) for every k ϵ ω, we have that either Bk,0 → ∀xPk,0(x) is 1-valid or Bk,0 → ∀xPk,1(x) is 1-valid. Let I be the set of all the k ϵ ω such that Bk,0 → ∀xPk,0(x) is 1-valid and 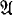 the first-order structure defined by
the first-order structure defined by 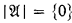 ,
, 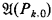
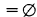 ,
, 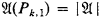 if k ϵ I and
if k ϵ I and 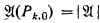 ,
, 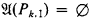 if k ∉ I.
if k ∉ I.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1979

