Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T06:57:42.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on Galois cohomology and definability

Published online by Cambridge University Press:  12 March 2014

Anand Pillay
Anand Pillay*
Affiliation:
Department of Mathematics, University of Illinois, 1409 West Green Street, Urbana, IL 61801, USA, E-mail: pillay@math.uiuc.edu
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we develop some basic features of Galois cohomology, specifically the connection between first Galois cohomology groups and principal homogeneous spaces, in a model-theoretic context. “Descent theory” also fits into our approach.

The model theory involved is elementary, and the reader is referred to [2]. It should be said that we make crucial use of Meq in our analysis. The reader is also referred to Poizat's seminal paper “Une theorie de Galois imaginaire” ([6]). Although our results do not depend on Poizat's work, it is in his paper that the model-theoretic context is suggested for a generalised treatment of Galois theory.

Nothing in this paper is particularly deep. We are concerned mainly with translating between the Galois cohomological language and the language of definable sets and definable families of definable sets. We will introduce (in a suitable context) the notion of a definable cocycle (from an automorphism group 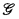to a definable group G). The (classical) situation of profinite 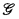and continuous cocycles will be a special case. Kolchin's theory of constrained cohomology will be another special case, and our results yield a substantially simpler proof of his Theorem 5 from Chapter VII of [4]. In any case model-theorists will see that definable cocycles correspond to objects with which they are already quite familiar—commuting families of definable bijections.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 2 , June 1997 , pp. 487 - 492
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chatelet, F., Methodes Galoisiennes et courbes de genre 1, Ann. Univ. Lyon Sect. A, vol. 89 (1946), pp. 40–49.Google Scholar
[2]Hodges, W. H., Model theory, vol. 42, Cambridge University Press, 1993.CrossRefGoogle Scholar
[3]Kolchin, E. R., Differential algebra and algebraic groups, Academic Press, 1973.Google Scholar
[4]Kolchin, E. R., Differential algebraic groups, Academic Press, 1985.Google Scholar
[5]Pillay, A., Some foundational questions concerning differential algebraic groups, submitted to Pacific Journal of Math.Google Scholar
[6]Poizat, B., Une theorie de Galois imaginaire, this Journal, vol. 48 (1983), pp. 1151–1170.Google Scholar
[7]Serre, J. P., Cohomologie Galoisienne, Lecture Notes, vol. 5, Springer-Verlag, 5th ed., 1994.Google Scholar