Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-11T09:54:05.476Z Has data issue: false hasContentIssue false
  • English
  • Français

RESTRICTED MAD FAMILIES

Published online by Cambridge University Press:  05 November 2019

OSVALDO GUZMÁN ,
MICHAEL HRUŠÁK  and
OSVALDO TÉLLEZ
OSVALDO GUZMÁN
Affiliation:
CENTRO DE CIENCIAS MATEMÁTICAS UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO CAMPUS MORELIA MORELIA, MICHOACÁN MÉXICO 58089E-mail: oguzman@matmor.unam.mx
MICHAEL HRUŠÁK
Affiliation:
CENTRO DE CIENCIAS MATEMÁTICAS UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO CAMPUS MORELIA MORELIA, MICHOACÁN MÉXICO 58089E-mail: michael@matmor.unam.mx
OSVALDO TÉLLEZ
Affiliation:
INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY CAMPUS CIUDAD DE MÉXICO. DEPARTAMENTO DE MATEMÁTICAS, CCM. CALLE DEL PUENTE 222 COL. EJIDOS DE HUIPULCO, TLALPAN C.P. 14380, CDMX MÉXICO 58089E-mail: osvaldot@itesm.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 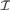${\cal I}$ be an ideal on ω. By cov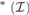${}_{}^{\rm{*}}({\cal I})$ we denote the least size of a family 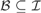${\cal B} \subseteq {\cal I}$ such that for every infinite 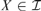$X \in {\cal I}$ there is 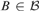$B \in {\cal B}$ for which 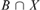$B\mathop \cap \nolimits X$ is infinite. We say that an AD family 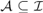${\cal A} \subseteq {\cal I}$ is a MAD family restricted to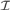${\cal I}$ if for every infinite 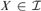$X \in {\cal I}$ there is 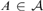$A \in {\cal A}$ such that 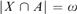$|X\mathop \cap \nolimits A| = \omega$. Let a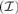$\left( {\cal I} \right)$ be the least size of an infinite MAD family restricted to 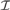${\cal I}$. We prove that If 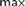$max${a,cov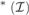${}_{}^{\rm{*}}({\cal I})\}$ then a$\left( {\cal I} \right) = {\omega _1}$, and consequently, if 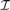${\cal I}$ is tall and 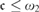$\le {\omega _2}$ then a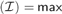$\left( {\cal I} \right) = max$ {a,cov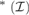${}_{}^{\rm{*}}({\cal I})\}$. We use these results to prove that if c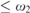$\le {\omega _2}$ then o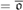$= \overline o$ and that as$= max${a,non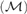$({\cal M})\}$. We also analyze the problem whether it is consistent with the negation of CH that every AD family of size ω1 can be extended to a MAD family of size ω1.

Keywords

03E1703E3503E05almost disjoint familiesMAD familiesidealsoff-branch
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 149 - 165
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham, U. and Magidor, M., Cardinal arithmetic, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), vol. 1, Springer, Dordrecht, 2010, pp. 1149–1227.Google Scholar
Balcar, B., Hernández-Hernández, F., and Hrušák, M., Combinatorics of dense subsets of the rationals. Fundamenta Mathematicae, vol. 183 (2004), no. 1, pp. 59–80.CrossRefGoogle Scholar
Balcar, B. and Simon, P., Disjoint refinement, Handbook of Boolean Algebras (Monk, J. D. and Bonnet, R., editors), vol. 2, North-Holland, Amsterdam, 1989, pp. 333–388.Google Scholar
Bartoszyński, T. and Judah, H., Set Theory: On the Structure of the Real Line, , A. K. Peters Ltd., Wellesley, MA, 1995. (English).CrossRefGoogle Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum, Handbook of Set Theory, vol. 1, 2, 3, Springer, Dordrecht, 2010, pp. 395–489.CrossRefGoogle Scholar
Brendle, J., Around splitting and reaping. Commentationes Mathematicae Universitatis Carolinae, vol. 39 (1998), no. 2, pp. 269–279.Google Scholar
Brendle, J., Mad families and iteration theory, Logic and Algebra (Zhang, Y., editor), Contemporary Mathematics, vol. 302, American Mathematical Society, Providence, RI, 2002, pp. 1–31.Google Scholar
Brendle, J. and Yatabe, S., Forcing indestructibility of MAD families. Annals of Pure and Applied Logic, vol. 132 (2005), no. 2–3, pp. 271–312.Google Scholar
Guzmán, O., Fuchino, S., Geshke, S., and Soukup, L., How to drive our families mad ?, preprint.Google Scholar
Guzmán, O., Hrušák, M., Martínez, C., and Ramos, A., Generic existence of MAD families, this Journal, vol. 82 (2017), no. 1, pp. 303–316.Google Scholar
Hernández-Hernández, F. and Hrušák, M., Cardinal invariants of analytic P-ideals. Canadian Journal of Mathematics, vol. 59 (2007), no. 3, pp. 575–595.CrossRefGoogle Scholar
Hrušák, M., Selectivity of almost disjoint families. Acta Universitatis Carolinae. Mathematica et Physica, vol. 41 (2000), no. 2, pp. 13–21.Google Scholar
Hrušák, M., Combinatorics of filters and ideals, Set Theory and its Applications (Babinkostova, L., Caicedo, A. E., Geschke, S., and Scheepers, M., editors), Contemporary Mathematics, vol. 533, American Mathematical Society, Providence, RI, 2011, pp. 29–69.CrossRefGoogle Scholar
Hrušák, M., Almost disjoint families and topology, Recent Progress in General Topology III (Hart, K. P., van Mill, J, and Simon, P., editors), Atlantis Press, Paris, 2014, pp. 601–638.CrossRefGoogle Scholar
Hrušák, M. and Ferreira, S. G., Ordering MAD families a la Katětov, this Journal, vol. 68 (2003), no. 4, pp. 1337–1353.Google Scholar
Hrušák, M., Meza-Alcántara, D., and Minami, H., Pair-splitting, pair-reaping and cardinal invariants of Fσ-ideals, this Journal, vol. 75 (2010), no. 2, pp. 661–677.Google Scholar
Hrušák, M. and Zapletal, J., Forcing with quotients. Archive for Mathematical Logic, vol. 47 (2008), no. 7–8, pp. 719–739.CrossRefGoogle Scholar
Kamburelis, A. and Weglorz, B., Splittings. Archive for Mathematical Logic, vol. 35 (1996), no. 4, pp. 263–277.CrossRefGoogle Scholar
Kurilić, M. S., Cohen-stable families of subsets of integers, this Journal, vol. 66 (2001), no. 1, pp. 257–270.Google Scholar
Leathrum, T. E., A special class of almost disjoint families, this Journal, vol. 60 (1995), no. 3, pp. 879–891.Google Scholar
Miller, A. W., Covering 2ω with ω1 disjoint closed sets, The Kleene Symposium (Barwise, J., Keisler, H. J., and Kunen, K., editors), Studies in Logic and the Foundations of Mathematics, vol. 101, Elsevier, Amsterdam, 1980, pp. 415–421.CrossRefGoogle Scholar
Newelski, L., On partitions of the real line into compact sets, this Journal, vol. 52 (1987), no. 2, pp. 353–359.Google Scholar
Shelah, S., Proper and Improper Forcing, second ed., Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.Google Scholar
Shelah, S., Two cardinal invariants of the continuum (d < a) and FS linearly ordered iterated forcing. Acta Mathematica, vol. 192 (2004), no. 2, pp. 187–223.CrossRefGoogle Scholar
Spinas, O., Partition numbers. Annals of Pure and Applied Logic, vol. 90 (1997), no. 1–3, pp. 243–262.CrossRefGoogle Scholar
Zapletal, J., Forcing Idealized, Cambridge Tracts in Mathematics, vol. 174, Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar