Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T17:40:08.971Z Has data issue: false hasContentIssue false
  • English
  • Français

A result concerning cardinalities of ultraproducts1

Published online by Cambridge University Press:  12 March 2014

H. Jerome Keisler  and
Karel Prikry
H. Jerome Keisler
Affiliation:
University of Wisconsin, Madison, Wisconsin 53706
Karel Prikry
Affiliation:
University of California, Los Angeles, California 90024
Get access Rights & Permissions [Opens in a new window]

Extract

The cardinality problem for ultraproducts is as follows: Given an ultrafilter 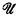over a set I and cardinals αi, i ∈ I, what is the cardinality of the ultraproduct 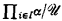? Although many special results are known, several problems remain open (see [5] for a survey). For example, consider a uniform ultrafilter 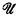over a set I of power κ (uniform means that all elements of 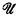have power κ). It is open whether every countably incomplete 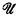has the property that, for all infinite α, the ultra-power 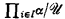has power ακ. However, it is shown in [4] that certain countably incomplete 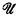, namely the κ-regular 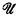, have this property.

This paper is about another cardinality property of ultrafilters which was introduced by Eklof [1] to study ultraproducts of abelian groups. It is open whether every countably incomplete ultrafilter has the Eklof property. We shall show that certain countably incomplete ultrafilters, the κ-good ultrafilters, do have this property. The κ-good ultrafilters are important in model theory because they are exactly the ultrafilters 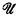such that every ultraproduct modulo 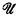is κ-saturated (see [5]).

Let 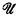be an ultrafilter on a set I. Let αi, n, i ∈ I, n ∈ ω, be cardinals and αi, n, ≥ αi, m if n < m. Let

.

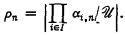Then ρn are nonincreasing and therefore there is some m and ρ such that ρn = ρ if n ≥ m. We call ρ the eventual value (abbreviated ev val) of ρn.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 1 , March 1974 , pp. 43 - 48
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The preparation of this paper was supported by NSF grants GP-27633 and GP-27964.

References

REFERENCES

[1]Eklof, P. C., The structure of uhraproducts of Abelian groups (to appear).Google Scholar
[2]Frolik, A., Sums of ultrafilters, Bulletin of the American Mathematical Society, vol. 73 (1967), pp. 87–91.CrossRefGoogle Scholar
[3]Keisler, H. J., Good ideals infields of sets, Annals of Mathematics, vol. 79 (1964), pp. 338–359.CrossRefGoogle Scholar
[4]Keisler, H. J., On cardinalities of uhraproducts, Bulletin of the American Mathematical Society, vol. 70 (1964), pp. 644–647.CrossRefGoogle Scholar
[5]Keisler, H. J., A survey of ultraproducts, Proceedings of the 1964 International Congress, North-Holland, Amsterdam, 1965, pp. 112–126.Google Scholar
[6]Keisler, H. J., Ideals with prescribed degree of goodness, Annals of Mathematics, vol. 81 (1965), pp. 112–116.CrossRefGoogle Scholar
[7]Keisler, H. J., Ultraproducts of finite sets, this Journal, vol. 32 (1967), pp. 47–57.Google Scholar
[8]Kunen, K., Ultrafilters and independent sets, Transactions of the American Mathematical Society, vol. 172 (1972), pp. 299–306.CrossRefGoogle Scholar
[9]Frayne, T., Morel, A. and Scott, D., Reduced direct products, Fundamenta Mathematicae, vol. 51 (1962), pp. 195–228.CrossRefGoogle Scholar
[10]Shelah, S., Saturation of ultrapowers and Keisler's order, Annals of Mathematical Logic, vol. 4 (1972), pp. 75–114.CrossRefGoogle Scholar