Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T19:44:02.372Z Has data issue: false hasContentIssue false
  • English
  • Français

A result of relative consistency about the predicate WO(δ, x)

Published online by Cambridge University Press:  12 March 2014

René David
René David*
Affiliation:
Université Toulouse le Mirail, Toulouse, France
Get access Rights & Permissions [Opens in a new window]

Extract

In [K] Keisler introduces a set theoretical relation WO(δ, x), where δ is an ordinal. This relation is characterized in ZF set theory by the following properties:

(1) WO(0, x) if and only if there is a wellordering on x.

(2) For δ > 0, WO(δ, x) if and only if there is a function ƒ with domain an ordinal λ such that:

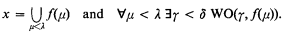
We denote WO∞ the collection denned by: WO∞(x) = ∃δ WO(δ, x).

In [K] Keisler shows that countable transitive models of ZF + ∃x ¬ WO∞(x) have transitive uncountable elementary extensions with the same ordinals. Moreover for transitive models, satisfying ∃x ¬ WO∞(x) is also a necessary condition for the existence of an elementary extension with the same ordinals. (See [K bis] and also [K-M] where the connection with forcing is analysed.)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 45 , Issue 3 , September 1980 , pp. 483 - 492
Copyright
Copyright © Association for Symbolic Logic 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[D]David, R., Résultats de consistence relative concernant les éssencés WO(α, x), Thèse de 3e cycle, Université de Paris VII, 1973.Google Scholar
[D bis]David, R., Note aux Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences, vol. 80 (1975), pp. 981–983.Google Scholar
[Gr]Grigorieff, S., Intermediate submodels and generic extensions in set theory, Annals of Mathematics, vol. 101 (1975), pp. 447–490.CrossRefGoogle Scholar
[K]Keisler, H. J., Logic with the quantifier “there exist uncountably many”, Annals of Mathematical Logic, vol. 1 (1970), pp. 1–93.CrossRefGoogle Scholar
[K bis]Keisler, H. J., Forcing and omitting types, Motley Symposium.Google Scholar
[Kr]Krivine, J. L., Cours de théorie des ensembles, notions de forcing, Université Paris VII, 1970.Google Scholar
[K-M]Krivine, J. L. and McAloon, K., Forcing and generalized quantifiers, Annals of Mathematical Logic, vol. 5 (1973), pp. 199–255.CrossRefGoogle Scholar
[S]Shoenfield, J. R., Unramified forcing, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13, part I (Scott, D., Editor), American Mathematical Society, Providence, Rhode Island, 1971, pp. 357–382.CrossRefGoogle Scholar