Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jäger, Gerhard
and
Strahm, Thomas
1995.
Second order theories with ordinals and elementary comprehension.
Archive for Mathematical Logic,
Vol. 34,
Issue. 6,
p.
345.
Rathjen, Michael
1998.
Logic Colloquium ’95.
Vol. 11,
Issue. ,
p.
275.
1998.
Handbook of Proof Theory.
Vol. 137,
Issue. ,
p.
209.
Feferman, Solomon
and
Strahm, Thomas
2000.
The unfolding of non-finitist arithmetic.
Annals of Pure and Applied Logic,
Vol. 104,
Issue. 1-3,
p.
75.
Afshari, Bahareh
and
Rathjen, Michael
2009.
Reverse mathematics and well-ordering principles: A pilot study.
Annals of Pure and Applied Logic,
Vol. 160,
Issue. 3,
p.
231.
Marcone, Alberto
and
Montalbán, Antonio
2009.
On Fraïssé’s conjecture for linear orders of finite Hausdorff rank.
Annals of Pure and Applied Logic,
Vol. 160,
Issue. 3,
p.
355.
Leigh, Graham Emil
and
Rathjen, Michael
2010.
An ordinal analysis for theories of self-referential truth.
Archive for Mathematical Logic,
Vol. 49,
Issue. 2,
p.
213.
Fujimoto, Kentaro
2010.
Relative Truth Definability of Axiomatic Truth Theories.
The Bulletin of Symbolic Logic,
Vol. 16,
Issue. 3,
p.
305.
Strahm, Thomas
2017.
Feferman on Foundations.
Vol. 13,
Issue. ,
p.
187.
Rahli, Vincent
Bickford, Mark
and
Constable, Robert L.
2017.
Bar induction: The good, the bad, and the ugly.
p.
1.
Rathjen, M.
2017.
Logic Colloquium '95.
p.
275.
Rahli, Vincent
Bickford, Mark
Cohen, Liron
and
Constable, Robert L.
2019.
Bar Induction is Compatible with Constructive Type Theory.
Journal of the ACM,
Vol. 66,
Issue. 2,
p.
1.
WALSH, JAMES
2024.
AN INCOMPLETENESS THEOREM VIA ORDINAL ANALYSIS.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 1,
p.
80.

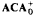 ,
, 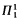 -sentences.
-sentences.