Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Enayat, Ali
2008.
A standard model of Peano arithmetic with no conservative elementary extension.
Annals of Pure and Applied Logic,
Vol. 156,
Issue. 2-3,
p.
308.
Gitman, Victoria
2009.
Proper and piecewise proper families of reals.
Mathematical Logic Quarterly,
Vol. 55,
Issue. 5,
p.
542.
Enayat, Ali
and
Shelah, Saharon
2011.
An improper arithmetically closed Borel subalgebra of P(ω) mod FIN.
Topology and its Applications,
Vol. 158,
Issue. 18,
p.
2495.

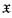 is proper if the quotient Boolean algebra
is proper if the quotient Boolean algebra 