Article contents
A second order version of S 2 i and U 2 1
Published online by Cambridge University Press: 12 March 2014
Extract
In [1] S. Buss introduced systems of bounded arithmetic 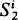 ,
,  ,
,  ,
, 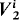 (i = 1, 2, 3, …).
(i = 1, 2, 3, …). 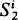 and
and  are first order systems and
are first order systems and  and
and 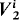 are second order systems.
are second order systems. 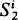 and
and  are closely related to
are closely related to 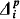 and
and 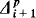 respectively in the polynomial hierarchy, and
respectively in the polynomial hierarchy, and  and
and 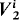 are closely related to PSPACE and EXPTIME respectively. One of the most important problems in bounded arithmetic is whether the hierarchy of bounded arithmetic collapses, i.e. whether
are closely related to PSPACE and EXPTIME respectively. One of the most important problems in bounded arithmetic is whether the hierarchy of bounded arithmetic collapses, i.e. whether 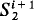 =
=  or
or  =
= 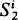 for some i, or whether
for some i, or whether 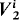 =
=  , or whether
, or whether  is a conservative extension of S 2 = ⋃i
is a conservative extension of S 2 = ⋃i 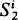 . These problems are relevant to the problems whether the polynomial hierarchy PH collapses or whether PSPACE = PH or whether PSPACE = EXPTIME. It was shown in [4] that
. These problems are relevant to the problems whether the polynomial hierarchy PH collapses or whether PSPACE = PH or whether PSPACE = EXPTIME. It was shown in [4] that  =
= 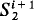 implies
implies 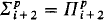 and consequently the collapse of the polynomial hierarchy. We believe that the separation problems of bounded arithmetic and the separation problems of computational complexities are essentially the same problem, and the solution of one of them will lead to the solution of the other.
and consequently the collapse of the polynomial hierarchy. We believe that the separation problems of bounded arithmetic and the separation problems of computational complexities are essentially the same problem, and the solution of one of them will lead to the solution of the other.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991
References
REFERENCES
- 2
- Cited by

