Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T02:26:54.012Z Has data issue: false hasContentIssue false
  • English
  • Français

SEMILATTICES AND THE RAMSEY PROPERTY

Published online by Cambridge University Press:  22 December 2015

MIODRAG SOKIĆ
MIODRAG SOKIĆ*
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS YORK UNIVERSITY TORONTO ON, CANADAE-mail: msokic@yorku.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider ${\cal S}$, the class of finite semilattices; 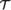${\cal T}$, the class of finite treeable semilattices; and 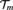${{\cal T}_m}$, the subclass of 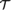${\cal T}$ which contains trees with branching bounded by m. We prove that 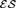${\cal E}{\cal S}$, the class of finite lattices with linear extensions, is a Ramsey class. We calculate Ramsey degrees for structures in ${\cal S}$, 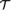${\cal T}$, and 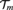${{\cal T}_m}$. In addition to this we give a topological interpretation of our results and we apply our result to canonization of linear orderings on finite semilattices. In particular, we give an example of a Fraïssé class 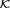${\cal K}$ which is not a Hrushovski class, and for which the automorphism group of the Fraïssé limit of 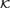${\cal K}$ is not extremely amenable (with the infinite universal minimal flow) but is uniquely ergodic.

Keywords

Primary: 05D1006A12Secondary: 37B0543A07semilatticesRamsey propertylinear orderings
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 4 , December 2015 , pp. 1236 - 1259
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Angel, O., Kechris, A. S., and Lyons, R., Random orderings and unique ergodicity of automorphism groups. arXiv:1208.2389.Google Scholar
Auslander, J., Minimal flows and their extensions, North Holland, Amsterdam, 1998.Google Scholar
Becker, H. and Kechris, A. S., The descriptive set theory of Polish group actions, Cambridge University Press, New York, 1996.CrossRefGoogle Scholar
Deuber, W., A Generalization of Ramsey’s theorem for regular trees. Journal of Combinatorial Theory, Series B, vol. 18 (1975), pp. 18–23.CrossRefGoogle Scholar
Deuber, W. and Rothschild, B., Categories without the Ramsey property. Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), vol. 1, pp. 225–249, Colloquia Mathematica Societatis Janos Bolyai, vol. 18, North-Holland, Amsterdam-New York, 1978.Google Scholar
Graham, R. L. and Rothschild, B. L., Ramsey’s theorem for n-parameter sets. Transactions of the American Mathematical Society, vol. 159 (1971) pp. 257–292.Google Scholar
Graham, R. L. and Rothschild, B. L., Some recent developments in Ramsey theory. Combinatorics (Proc. Advanced Study Inst., Breukelen, 1974), Part 2: Graph theory; foundations, partitions and combinatorial geometry, Mathematical Centre tracts, No. 56, Mathematisch Centrum, Amsterdam, pp. 61–76, 1974.Google Scholar
Graham, R. L., Leeb, K., and Rothschild, B. L., Ramsey’s theorem for a class of categories. Advances in Mathematics, vol. 8 (1972), pp. 417–433.CrossRefGoogle Scholar
Hodges, W., Model theory, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Ježek, J. and Nešetřil, J., Ramsey varieties. European Journal of Combinatorics, vol. 4 (1983), no. 2, pp. 143–147.CrossRefGoogle Scholar
Kechris, A. S., Pestov, V., and Todorčević, S., Fraïssé limits, Ramsey theory, and topological dynamics of automorphism groups. Geometric and Functional Analysis, vol. 15 (2005), pp. 106–189.CrossRefGoogle Scholar
Malicki, M., The automorphism group of the random lattice in not amenable. Fundamenta Mathematicae, vol. 226 (2014), pp. 245–252.CrossRefGoogle Scholar
Milliken, K. R., A Ramsey theorem for trees. Journal of Combinatorial Theory, Series A, vol. 26 (1979), no. 3, pp. 215–237.CrossRefGoogle Scholar
Nešetřil, J., Prömel, H. J., Rödl, V., and Voigt, B., Note on canonizing ordering theorems for Hales Jewett structures, Proceedings of the 11th winter school on abstract analysis (Železná Ruda, 1983), Rendiconti del Circolo Matematico di Palermo, vol. 2, Suppl. No. 3, pp. 191–196, 1984.Google Scholar
Nešetřil, J. and Rödl, V., Combinatorial partitions of finite posets and lattices—Ramsey lattices. Algebra Universalis, vol. 19 (1984), no. 1, pp. 106–119.CrossRefGoogle Scholar
Nguyen Van The, L., More on Kechris-Pestov-Todorcevic correspondence: Precompact Expansions. ArXiv: 1201.1270v2, March 2012. Reviewed Nguyen Van Thé, L.More on the Kechris-Pestov-Todorcevic correspondence: Precompact expansions. Fundamenta Mathematicae, vol. 222 (2013), no. 1, pp. 19–47.CrossRefGoogle Scholar
Prömel, H. J., Some remarks on natural orders for combinatorial cubes. Proceedings of the Oberwolfach Meeting “Kombinatorik” (1986), Discrete mathematics, vol. 73 (1989), no. 1–2, pp. 189–198.CrossRefGoogle Scholar
Roman, S., Lattices and ordered sets, Springer, New York, 2008.Google Scholar
Ramsey, F. P., On a Problem of Formal Logic. Proceedings of the London Mathematical Society, vol. S2-30, no. 1, p. 264.CrossRefGoogle Scholar
Sokić, M., Ramsey property of finite posets. Order, vol. 29 (2012), no. 1, pp. 1–30.CrossRefGoogle Scholar
Sokić, M., Ramsey property of finite posets II. Order, vol. 29 (2012), no. 1, pp. 31–47.CrossRefGoogle Scholar
Sokić, M., Unary functions, under review.Google Scholar
Solecki, S., Abstract Approach to Ramsey Theory and Ramsey Theorems for Finite Trees, Asymptotic Geometric Analysis, Fields Institute Communications, Springer, Berlin, 2013, pp. 313–340.CrossRefGoogle Scholar
Todorčević, S., Introduction to Ramsey spaces. Annals of Mathematics Studies, vol. 174, Princeton University Press, New Jersey, 2010.CrossRefGoogle Scholar
Zucker, A., Amenability and Unique Ergodicity of Automorphism Groups of Fraïssé Structures, arXiv:1304.2839v2.Google Scholar