Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T19:24:55.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple and hyperhypersimple vector spaces1

Published online by Cambridge University Press:  12 March 2014

Allen Retzlaff
Allen Retzlaff*
Affiliation:
Cornell University, Ithaca, NY 14853 State University of New York, Purchase, NY 10577
Get access Rights & Permissions [Opens in a new window]

Abstract

Let V∞ be a fixed, fully effective, infinite dimensional vector space. Let 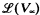be the lattice consisting of the recursively enumerable (r.e.) subspaces of V∞, under the operations of intersection and weak sum (see §1 for precise definitions). In this article we examine the algebraic properties of .

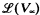Early research on recursively enumerable algebraic structures was done by Rabin [14], Frölich and Shepherdson [5], Dekker [3], Hamilton [7], and Guhl [6]. Our results are based upon the more recent work concerning vector spaces of Metakides and Nerode [12], Crossley and Nerode [2], Remmel [15], [16], and Kalantari [8].

In the main theorem below, we extend a result of Lachlan from the lattice 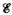of r.e. sets to 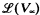. We define hyperhypersimple vector spaces, discuss some of their properties and show if A, B ∈ 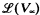, and A is a hyperhypersimple subspace of B then there is a recursive space C such that A + C = B. It will be proven that if V ∈ 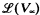and the lattice of superspaces of V is a complemented modular lattice then V is hyperhypersimple. The final section contains a summary of related results concerning maximality and simplicity.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 2 , June 1978 , pp. 260 - 269
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This research was partially supported by NSF grant number MPS 74-06378.

References

REFERENCES

[0]Birkhoff, G., Lattice theory, American Mathematical Society Colloquium Publications, vol. 25 (1967), Providence R. I.Google Scholar
[1]Crossley, J. N. and Nerode, A., Combinatorial functors, Springer-Verlag, Berlin and New York, 1974.CrossRefGoogle Scholar
[2]Crossley, J. N. and Nerode, A., Effective dimension, Journal of Algebra, vol. 41 (1976), pp. 398–412.CrossRefGoogle Scholar
[3]Dekker, J. C. E., Countable vector spaces with recursive operations, I, II, this Journal, vol. 34 (1969), pp. 363–387 and vol. 36 (1971), pp. 477–493.Google Scholar
[4]Friedberg, R. M., Three theorems on recursive enumeration, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[5]Frölich, A. and Shepherdson, J. C., Effective procedures in field theory,. Philosophical Transactions of the Royal Society of London, Series A, vol. 284 (1955), pp. 407–432.Google Scholar
[6]Guhl, R., Two types of recursively enumerable vector spaces, Ph.D. dissertation, Rutgers University, 1973.Google Scholar
[7]Hamilton, A. G., Bases and α-dimensions of countable vector spaces with recursive operations, this Journal, vol. 35 (1970), pp. 85–96.Google Scholar
[8]Kalantari, I., Structural properties of the lattice of recursively enumerable vector spaces, Ph.D. dissertation, Cornell University, 1976.Google Scholar
[9]Kalantari, I. and Retzlaff, A., Maximal vector spaces under automorphisms of the lattice of recursively enumerable vector spaces, this Journal, vol. 42 (1977), pp. 481–491.Google Scholar
[10]Lachlan, A. H., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.CrossRefGoogle Scholar
[11]Metakides, G. and Nerode, A., Recursion theory and algebra, Algebra and logic, Lecture Notes in Mathematics, no. 450, Springer-Verlag, Berlin and New York, 1975, pp. 209–219.CrossRefGoogle Scholar
[12]Metakides, G. and Nerode, A., Recursively enumerable vector spaces, Annals of Mathematical Logic, vol. 11 (1977), pp. 147–171.CrossRefGoogle Scholar
[13]Morley, M. D. and Soare, R. I., Boolean algebras, splitting theorems, and Δ20 sets, Fundamenta Mathematicae, vol. 90 (1975), pp. 45–52.CrossRefGoogle Scholar
[14]Rabin, M. O., Computable algebra, general theory and theory of computable fields, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
[15]Remmel, J., Co-recursively enumerable structures, Ph.D. dissertation, Cornell University, 1974.Google Scholar
[16]Remmel, J., On vector spaces with no extendible bases, this Journal (to appear).Google Scholar
[17]Retzlaff, A., Recursive and simple vector spaces, Ph.D. dissertation, Cornell University, 1976.Google Scholar
[18]Retzlaff, A., Direct summands of r.e. vector spaces, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik (to appear).Google Scholar
[19]Rogers, H., Theory of recursive functions and effective computabitity, McGraw-Hill, New York, 1968.Google Scholar
[20]Sacks, G. E., Degrees of unsolvability (revised edition), Annals of Mathematical Studies, no. 55, Princeton University Press, Princeton, New Jersey, 1966.Google Scholar
[21]Soare, R. I., Automorphisms of the lattice of recursively enumerable sets, Part I: Maximal sets, Annals of Mathematics, vol. 100 (1974), p. 80–120.CrossRefGoogle Scholar