Hostname: page-component-7dd5485656-gs9qr Total loading time: 0 Render date: 2025-10-31T00:28:59.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Skolem functions and elementary embeddings

Published online by Cambridge University Press:  12 March 2014

Julia F. Knight
Get access Rights & Permissions [Opens in a new window]

Extract

Let L be an elementary first order language. Let 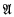be an L-structure, and let φ be an L-formula with free variables u1, …, un, and υ. A Skolem function for φ on 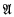is an n-ary operation f on 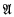such that for all 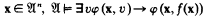. If 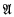is an elementary substructure of 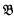, then an n-ary operation f on 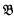is said to preserve the elementary embedding of 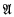into 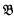if f(x)∈ 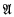for all x ∈ 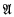n, and (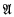, f ∣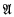n) ≺ (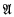, f). Keisler asked the following question:

Problem 1. If 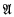and 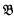are L-structures such that 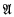≺ 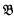, and if φ (u, υ) is an L-formula (with appropriate free variables), must there be a Skolem function for φ on 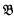which preserves the elementary embedding?

Payne [6] gave a counterexample in which the language L is uncountable. In [3], [5], the author announced the existence of an example in which L is countable but the structures 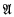and 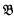are uncountable. The construction of the example will be given in this paper. Keisler's problem is still open in case both the language and the structures are required to be countable. Positive results for some special cases are given in [4].

The following variant of Keisler's question was brought to the author's attention by Peter Winkler:

Problem 2. If L is a countable language, 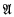a countable L-structure, and φ(u, υ) an L-formula, must there be a Skolem function f for φ on 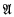such that for every countable elementary extension 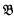of 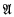, there is an extension of f which preserves the elementary embedding of 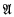into ?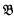

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 1 , March 1977 , pp. 94 - 98
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[2]Fichtenholz, G. and Kantorovitch, L., Sur les opérations dans l'espace des fonctions bornées, Studio Mathematica, vol. 5 (1934), pp. 69–98.CrossRefGoogle Scholar
[3]Knight, J., An example involving Skolem functions and elementary embeddings, Notices of the American Mathematical Society, vol. 17 (1970), p. 964.Google Scholar
[4]Knight, J., Some problems in model theory, Doctoral dissertation, University of California, Berkeley, 1972.Google Scholar
[5]Knight, J., Generic expansions of structures, this Journal, vol. 38 (1973), pp. 561–570.Google Scholar
[6]Payne, T. H., An elementary submodel never preserved by Skolem expansions, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 15 (1969), pp. 435–436.CrossRefGoogle Scholar