Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schindler, Ralf
and
Schlicht, Philipp
2011.
Thin equivalence relations in scaled pointclasses.
Mathematical Logic Quarterly,
Vol. 57,
Issue. 6,
p.
615.
Schlicht, Philipp
2014.
Thin equivalence relations and inner models.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 10,
p.
1577.
Kechris, Alexander S.
Löwe, Benedikt
and
Steel, John R.
2020.
Large Cardinals, Determinacy and Other Topics.
Rudominer, Mitch
2025.
The mouse set theorem just past projective.
Journal of Mathematical Logic,
Vol. 25,
Issue. 02,

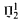 determinacy implies that for every thin
determinacy implies that for every thin 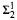 equivalence relation there is a
equivalence relation there is a 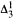 real,
real, 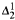 (
(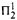 prewellorder has rank less than
prewellorder has rank less than 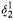 .
.