Article contents
Some formal relative consistency proofs
Published online by Cambridge University Press: 12 March 2014
Extract
These systems are roughly natural number theory in, respectively, nth order function calculus, for all positive integers n. Each of these systems is expressed in the notation of the theory of types, having variables with type subscripts from 1 to n. Variables of type 1 stand for natural numbers, variables of type 2 stand for classes of natural numbers, etc. Primitive atomic wff's (well-formed formulas) of Tn are those of number theory in variables of type 1, and of the following kind for n > 1: xi ϵ yi+1. Other wff's are formed by truth functions and quantifiers in the usual manner. Quantification theory holds for all the variables of Tn. Tn has the axioms Z1 to Z9, which are, respectively, the nine axioms and axiom schemata for the system Z (natural number theory) on p. 371 of [1]. These axioms and axiom schemata contain only variables of type 1, except for the schemata Z2 and Z9, which are as follows:
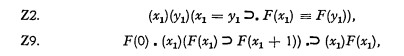
where ‘F(x1)’ can be any wff of Tn. Identity is primitive for variables of type 1; for variables of other types it is defined as follows:
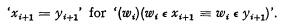
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953
References
BIBLIOGRAPHY
- 5
- Cited by

