Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T17:32:59.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Some interesting connections between the slow growing hierarchy and the Ackermann function

Published online by Cambridge University Press:  12 March 2014

Andreas Weiermann
Andreas Weiermann*
Affiliation:
Institut für Mathematische Logik und Grundlagenforschung, Der Westfällschen Wilhelms-Universität Münster, Einsteinstr, 62, D-48149 Münster, Germany, E-mail: weierma@math.uni-muenster.de
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that the so called slow growing hierarchy depends non trivially on the choice of its underlying structure of ordinals. To this end we investigate the growth rate behaviour of the slow growing hierarchy along natural subsets of notations for Γ0. Let T be the set-theoretic ordinal notation system for Γ0 and Ttree the tree ordinal representation for Γ0. It is shown in this paper that (Gα)α∈T matches up with the class of functions which are elementary recursive in the Ackermann function as does 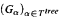(by folklore). By thinning out terms in which the addition function symbol occurs we single out subsystems T* ⊆ T and Ttree* ⊆ Ttree (both of order type not exceeding ε0) and prove that 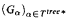still matches up with 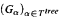but 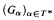now consists of elementary recursive functions only. We discuss the relationship between these results and the Γ0-based termination proof for the standard rewrite system for the Ackermann function.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 2 , June 2001 , pp. 609 - 628
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aczel, P., Another elementary treatment of Girard’s result connecting the slow and fast growing hierarchies of number-theoretic functions, 1980, Manuscript.Google Scholar
[2]Arai, T., A slow growing analogue to Buchholz’ proof, Annals of Pure and Applied Logic, vol. 54 (1991), pp. 101–120.CrossRefGoogle Scholar
[3]Arai, T., Some results on cut-elimination, provable well-orderings, induction and reflection, Annals of Pure and Applied Logic, vol. 95 (1998), pp. 93–184.CrossRefGoogle Scholar
[4]Buchholz, W., Fundamentalfolgen für , Preprint, München, 1980.Google Scholar
[5]Buchholz, W., Three contributions to the conference on recent advances in proof theory, Oxford, 1980, mimeographed.Google Scholar
[6]Buchholz, W., Proof-theoretic analysis of termination proofs, Annals of Pure and Applied Logic, vol. 75 (1995), no. 1-2, pp. 57–66.CrossRefGoogle Scholar
[7]Buchholz, W., Cichon, E. A., and Weiermann, A., A uniform approach to fundamental sequences and hierarchies, Mathematical Logic Quarterly, vol. 40 (1994), pp. 273–286.CrossRefGoogle Scholar
[8]Cichon, A., Termination orderings and complexity characterisations, Proof theory (Aczel, P.et al., editors), Cambridge University Press, Cambridge, 1992, pp. 171–193.Google Scholar
[9]Cichon, E. A. and Wainer, S. S., The slow-growing and the Grzegorczyk hierarchies, this Journal, vol. 48 (1983), pp. 399–408.Google Scholar
[10]Dennis-Jones, E.C. and Wainer, S.S., Subrecursive hierarchies via direct limits, Computation and proof theory, Springer, Berlin, 1984, pp. 118–128.Google Scholar
[11]Dershowitz, N. and Jouannaud, J.P., Rewrite systems, Handbook of theoretical computer science, Elsevier, Amsterdam, 1990, pp. 243–320.Google Scholar
[12]Feferman, S., Systems of predicative analysis, II: Representations of ordinals, this Journal, vol. 33 (1968), pp. 193–220.Google Scholar
[13]Girard, J.-Y., -logic. I. Dilators, Annals of Mathematical Logic, vol. 21 (1981), pp. 75–219.CrossRefGoogle Scholar
[14]Hofbauer, D., Termination proofs by multiset path orderings imply primitive recursive derivation lengths, Proceedings of the 2nd algebraic and logic programming, Lecture Notes in Computer Science 463, Springer, Berlin, 1990, pp. 347–358.CrossRefGoogle Scholar
[15]Jervell, H.R., Homogeneous Trees, Lecture Notes at the University of München, 1979.Google Scholar
[16]Schmerl, U.R., Über die schwach und die stark wachsende Hierarchie zahlentheoretischer Funktionen, Sitzungsberichte der Bayerischen Akademie der Wissenschaften. Mathematisch-Naturwissenschaftliche Klasse, (1981), pp. 1–18.Google Scholar
[17]Schmidt, D., Well-Partial Orderings and Their Maximal Order Types, Habilitationsschrift, Heidelberg, 1979.Google Scholar
[18]Schütte, K., Primitiv-rekursive Ordinalzahlfunktionen, Sitzungsberichte der Bayerischen Akademie der Wissenschaften, Mathematisch Naturwissenschaftliche Klasse, (1975), pp. 143–153 (1976).Google Scholar
[19]Schütte, K., Proof theory, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
[20]Schwichtenberg, H., Homogeneous Trees and Subrecursive Hierarchies, Lecture at the University of München, 1980.Google Scholar
[21]Veblen, O., Continuous increasing functions of finite and transfinite ordinals, Transactions of the American Mathematical Society, vol. 9 (1908), pp. 280–292.CrossRefGoogle Scholar
[22]Vogel, H., Ausgezeichnete Folgen für prädikative Ordinalzahlen und prädikativ-rekursive Funktionen, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 23 (1977), pp. 435–438.CrossRefGoogle Scholar
[23]Wainer, S.S., Ordinal recursion, and a refinement of the extended Grzegorczyk hierarchy, this Journal, vol. 37 (1972), no. 2, pp. 281–292.Google Scholar
[24]Wainer, S.S., A subrecursive hierarchy over the predicative ordinals, Conference in mathematical logic — london ’70, Springer Lecture Notes in Mathematics 255, 1972, pp. 350–351.Google Scholar
[25]Wainer, S.S., Slow growing versus fast growing, this Journal, vol. 54 (1989), no. 2, pp. 608–614.Google Scholar
[26]Weiermann, A., Ein beitrag zur theorie der subrekursiven funktionen, Habilitationsschrift, Münster, 1994.Google Scholar
[27]Weiermann, A., Termination proofs for term rewriting systems by lexicographic path orderings imply multiply recursive derivation lengths, Theoretical Computer Science, vol. 139 (1995), pp. 355–362.CrossRefGoogle Scholar
[28]Weiermann, A., Γ0 may be minimal subrecursively inaccessible, Preprint, Münster, 1999.Google Scholar
[29]Weiermann, A., What makes the slow growing hierarchy slow growing?, London Mathematical Society: Sets and Proofs (Cooper, and Truss, , editors), Cambridge University Press, 1999, pp. 403–423.CrossRefGoogle Scholar