Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-10T07:08:53.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Some local definability results on countable topological structures1

Published online by Cambridge University Press:  12 March 2014

Holger Eisenmenger
Holger Eisenmenger*
Affiliation:
Seminar für Logik und Grundlagenforschung an der Universität Bonn, Bonn, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

L denotes a fixed finitary similarity type, B, respectively P a new relation symbol, 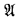an L-structure in the usual sense, and (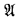, σ) a topological L-structure, where σ is a topology on A. (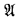, σ) is countable if 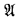is countable and σ has a countable base. The formal language for our study of topological structures is 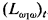. 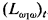is the least fragment of the (monadic) second-order, infinitary language 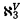closed under negation (⇁), countable disjunction (∨), countable conjunction (∧), quantification over individual variables (∃ν, ∀ν), and quantification over set variables in the form ∃V(t ∈ V → φ) [respectively ∃V(t ∈ V → φ] where t is an L-term and each free occurrence of V in φ is negative [respectively positive]. We abbreviate ∃V(t ∈ V ∧ φ) and ∀V(t ∈ V → φ) by ∃V ∈ ν φ respectively ∀V ∈ ν φ. (For detailed information on 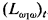we reIer to [1].)

i, j, … m, n range over ω. a, x, etc. denote finite tuples; a ∈ A means that all members of a are in A. IdA denotes the identity on A, Perm(A) the set of all permutations of A, and Aut(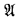) (respectively Aut(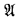, σ)) the set of all automorphisms of 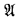(respectively (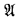σ)). Let F ⊆ Perm(A), B ⊆ Am(m ≥ 1), and μ be a system of subsets of A. B (respectively μ) is called invariant under F if for all ƒ ∈ F, ƒ(B) = B (respectively ƒ(μ) = μ). 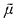denotes the least system of subsets of A which contains μ and which is closed under arbitrary union, .

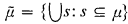For the rest of this paragraph let A be a countable nonempty set.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 3 , September 1983 , pp. 683 - 692
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The results obtained in this paper form a portion of the author's Diplomarbeit written under Professor M. Ziegler, to whom the author is indebted for his aid and encouragement.

References

REFERENCES

[1]Flum, J. and Ziegler, M., Topological model theory, Lecture Notes in Mathematics, vol. 769, Springer-Verlag, Berlin, 1980.Google Scholar
[2]Harnik, V., Game sentences, recursive saturation, definability, this Journal, vol. 45 (1980), pp. 35–46.Google Scholar
[3]Harnik, V. and Makkai, M., Applications of Vaught sentences and the covering theorem, this Journal, vol. 41 (1976), pp. 171–187.Google Scholar
[4]Kueker, D.W., Definability, automorphisms and infinitary languages, Lecture Notes in Mathematics, vol. 72, Springer-Verlag, Berlin, 1968, pp. 152–165.Google Scholar
[5]Makkai, M., Global definability theory in , Bulletin of the American Mathematical Society, vol. 79 (1973), pp. 916–921.CrossRefGoogle Scholar
[6]Reyes, G.E., Local definability theory, Annals of Mathematical Logic, vol. 1 (1970), pp. 95–137.CrossRefGoogle Scholar
[7]Scott, D., Logic with denumerably long formulas and finite strings of quantifiers, The Theory of Models, North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
[8]Ziegler, M., Definable bases of monotone systems, in: Logic Colloquium ‘77 (Macintyre, A., Pacholski, L. and Paris, J., Editors), Studies in Logic and Foundations of Mathematics, vol. 96, North-Holland, Amsterdam, 1978, pp. 296–311.Google Scholar