Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T02:51:48.159Z Has data issue: false hasContentIssue false
  • English
  • Français

Some model theory for game logics1

Published online by Cambridge University Press:  12 March 2014

Judy Green
Judy Green*
Affiliation:
Rutgers, The State University, Camden, New Jersey 08102
Get access Rights & Permissions [Opens in a new window]

Extract

Consistency properties and their model existence theorems have provided an important method of constructing models for fragments of L∞ω. In [E] Ellentuck extended this construction to Suslin logic. One of his extensions, the Borel consistency property, has its extra rule based not on the semantic interpretation of the extra symbols but rather on a theorem of Sierpinski about the classical operation 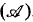. In this paper we extend that consistency property to the game logic LG and use it to show how one can extend results about 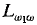and its countable fragments to LG and certain of its countable fragments. The particular formation of LG which we use will allow in the game quantifier infinite alternation of countable conjunctions and disjunctions as well as infinite alternation of quantifiers. In this way LG can be viewed as an extension of Suslin logic.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 2 , June 1979 , pp. 147 - 152
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The research for this paper was done while the author was a visitor at Howard University with financial support from the Rutgers University Faculty Academic Study Program.

References

REFERENCES

[Ba]Barwise, K. J., Absolute logics and L∞ω, Annals of Mathematical Logic, vol. 4 (1972), pp. 309–349.CrossRefGoogle Scholar
[Bu]Burgess, J. P., On the Hanf number of Souslin logic, this Journal, vol. 43 (1978), pp. 568–571.Google Scholar
[E]Ellentuck, E., The foundations of Suslin logic, this Journal, vol. 40 (1975), pp. 567–575.Google Scholar
[Ke]Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[Ku]Kurotowski, K., Topology, vol. I, Academic Press, New York, 1966.Google Scholar
[M]Moschovakis, Y. N., Elementary induction on abstract structures, North-Holland, Amsterdam, 1974.Google Scholar
[T]Takeuti, G., A determinate logic, The syntax and semantics of infinitary languages, Springer-Verlag, Berlin and New York, 1968, pp. 237–264.CrossRefGoogle Scholar
[V]Vaught, R. L., Descriptive set theory in , Cambridge Summer School in Mathematical Logic, Springer-Verlag, Berlin and New York, 1973, pp. 574–598.CrossRefGoogle Scholar
[V2]Vaught, R. L., Invariant sets in topology and logic, Fundamenta Mathematicae, vol. 82 (1974), pp. 270–294.CrossRefGoogle Scholar