Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T13:05:52.825Z Has data issue: false hasContentIssue false
  • English
  • Français

A sound and complete axiomatization for Dynamic Topological Logic

Published online by Cambridge University Press:  08 April 2017

David Fernández-Duque
David Fernández-Duque*
Affiliation:
Group for Computational Logic, Universidad de Sevilla, Ets de Ingeniería Informática, Calle Reina Mercedes S/N, 41012 Sevilla, Spain, E-mail: dfduque@us.es
Get access Rights & Permissions [Opens in a new window]

Abstract

Dynamic Topological Logic (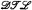) is a multimodal system for reasoning about dynamical systems. It is defined semantically and, as such, most of the work done in the field has been model-theoretic. In particular, the problem of finding a complete axiomatization for the full language of 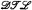over the class of all dynamical systems has proven to be quite elusive.

Here we propose to enrich the language to include a polyadic topological modality, originally introduced by Dawar and Otto in a different context. We then provide a sound axiomatization for 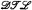over this extended language, and prove that it is complete. The polyadic modality is used in an essential way in our proof.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 3 , September 2012 , pp. 947 - 969
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Artemov, S. N., Davoren, J. M., and Nerode, A., Modal logics and topological semantics for hybrid systems, Technical Report MSI 97-05, Cornell University, 1997.CrossRefGoogle Scholar
[2]Bezhanishvili, Guram, Esakia, Leo, and Gabelaia, David, Some results on modal axiomatization and definability for topological spaces, Studia Logica, vol. 81 (2005), no. 3, pp. 325–355.CrossRefGoogle Scholar
[3]Bezhanishvili, Guram and Gehrke, Mai, Completeness of S4 with respect to the real line: revisited, Annuls of Pure and Applied Logic, vol. 131 (2005), no. 1–3, pp. 287–301.CrossRefGoogle Scholar
[4]Dawar, A. and Otto, M., Modal characterisation theorems over special classes of frames, Annals of Pure and Applied Logic, vol. 161 (2009), pp. 1–42, Extended journal version LICS 2005 paper.CrossRefGoogle Scholar
[5]Fernández-Duque, D., Non-deterministic semantics for dynamic topological logic, Annals of Pure and Applied Logic, vol. 157 (2009), no. 2–3, pp. 110–121, Kurt Gödel Centenary Research Prize Fellowships.CrossRefGoogle Scholar
[6]Fernández-Duque, D., Absolute completeness of S4u for its measure-theoretic semantics., Advances in modal logic, College Publications, 2010, pp. 100–119.Google Scholar
[7]Fernández-Duque, D., Dynamic topological logic interpreted over minimal systems, Journal of Philosophical Logic, vol. 40 (2011), no. 6, pp. 767–804.CrossRefGoogle Scholar
[8]Fernández-Duque, D., On the modal definability of simulability by finite transitive models, Studia Logica, vol. 98 (2011), no. 3, pp. 347–373.CrossRefGoogle Scholar
[9]Fernández-Duque, D., Tangledmodal logic for spatial reasoning, Proceedings of IJCAI (Walsh, T., editor), 2011, pp. 857–862.Google Scholar
[10]Fernández-Duque, D., Dynamic topological logic interpreted over metric spaces, this Journal, vol. 77 (2012), no. 1, pp. 308–328.Google Scholar
[11] Fernández-Duque, D., Tangled modal logic for topological dynamics. Annals of Pure and Applied Logic, vol. 163 (2012), no. 4, pp. 467–481.CrossRefGoogle Scholar
[12]Gabelaia, D., Kurucz, A., Wolter, F., and Zakharyaschev, M., Non-primitive recursive decidability of products of modal logics with expanding domains, Annals of Pure and Applied Logic, vol. 142 (2006), no. 1–3, pp. 245–268.CrossRefGoogle Scholar
[13]Konev, B., Kontchakov, R., Wolter, F., and Zakharyaschev, M., Dynamic topological logics over spaces with continuous functions, Advances in modal logic (Governatori, G., Hodkinson, I., and Venema, Y., editors), vol. 6, College Publications, 2006, pp. 299–318.Google Scholar
[14]Konev, B., Kontchakov, R., Wolter, F., and Zakharyaschev, M., On dynamic topological and metric logics, Studia Logica, vol. 84 (2006), pp. 129–160.CrossRefGoogle Scholar
[15]Kremer, P., Dynamic topological S5, Annals of Pure and Applied Logic, vol. 160 (2009), pp. 96–116.CrossRefGoogle Scholar
[16]Kremer, P., Strong completeness of SA wrt the real line, 2012.Google Scholar
[17]Kremer, P. and Mints, G., Dynamic topological logic, Annals of Pure and Applied Logic, vol. 131 (2005), pp. 133–158.CrossRefGoogle Scholar
[18]Kurucz, A., Wolter, F., Zakharyaschev, M., and Gabbay, Dov M., Many-dimensional modal logics: Theory and applications, 1 ed., Studies in Logic and the Foundations of Mathematics, vol. 148, North Holland, 2003.Google Scholar
[19]Lando, Tamar, Completeness of S4 for the Lebesgue measure algebra, Journal of Philosophical Logic, (2010).Google Scholar
[20]Lichtenstein, O. and Pnueli, A., Prepositional temporal logics: Decidability and completeness, Logic Journal of the IGPL, vol. 8 (2000), no. 1, pp. 55–85.CrossRefGoogle Scholar
[21]Mints, G. and Zhang, T., Prepositional logic of continuous transformations in Cantor space, Archive for Mathematical Logic, vol. 44 (2005), pp. 783–799.CrossRefGoogle Scholar
[22]Pnueli, A., The temporal logic ofprograms, Proceedings 18th IEEE symposium on the foundations of computer science, 1977, pp. 46–57.Google Scholar
[23]Prior, A., Time and modality, Oxford University Press, 1957.Google Scholar
[24]Tarski, A., Der Aussagenkalkül und die Topologie, Fundamenta Mathematica, vol. 31 (1938), pp. 103–134.CrossRefGoogle Scholar