Article contents
A special class of almost disjoint families
Published online by Cambridge University Press: 12 March 2014
Abstract
The collection of branches (maximal linearly ordered sets of nodes) of the tree <ωω (ordered by inclusion) forms an almost disjoint family (of sets of nodes). This family is not maximal — for example, any level of the tree is almost disjoint from all of the branches. How many sets must be added to the family of branches to make it maximal? This question leads to a series of definitions and results: a set of nodes is off-branch if it is almost disjoint from every branch in the tree; an off-branch family is an almost disjoint family of off-branch sets; and 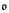 is the minimum cardinality of a maximal off-branch family.
is the minimum cardinality of a maximal off-branch family.
Results concerning 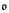 include: (in ZFC)
include: (in ZFC) 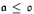 , and (consistent with ZFC)
, and (consistent with ZFC) 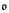 is not equal to any of the standard small cardinal invariants
is not equal to any of the standard small cardinal invariants 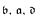 or
or 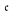 = 2ω. Most of these consistency results use standard forcing notions—for example,
= 2ω. Most of these consistency results use standard forcing notions—for example, 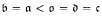 in the Cohen model.
in the Cohen model.
Many interesting open questions remain, though—for example, whether 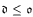 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 3
- Cited by

