Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T19:49:09.503Z Has data issue: false hasContentIssue false
  • English
  • Français

A splitting theorem for simple Π11 Sets

Published online by Cambridge University Press:  12 March 2014

James C. Owings Jr
James C. Owings Jr*
Affiliation:
University of Maryland,College Park, Maryland 20742
Get access Rights & Permissions [Opens in a new window]

Extract

As was first mentioned in [3, §5], if A is any 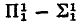– 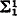set, A is the union of two disjoint 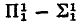– 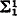sets B(0), B(1). In metarecursion theory this is proven as follows. Let ƒ be a one-to-one metarecursive function whose range is A, let R be an unbounded metarecursive set whose complement is also unbounded, and set B(0) = f(R), B(1) = f(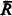). The corresponding fact of ordinary recursion theory, namely that any r.e. but not recursive set can be split into two other such sets, was proved by Friedberg [2, Theorem 1], using a clever priority argument. Sacks [7, Corollary 2] then showed that any r.e. but not recursive set is the union of two disjoint r.e. sets neither of which was recursive in the other, a much stronger result. In this paper we attempt to prove the analogous result for 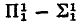– 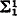sets A, but succeed only in the case A is simple; i.e., the complement of A contains no infinite 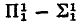subset. As a corollary we show the 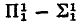metadegrees are dense, a fact already announced by Sacks [8, Corollary 1], but only proven by him for nonzero 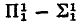metadegrees.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 3 , September 1971 , pp. 433 - 438
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Driscoll, G. C. Jr., Metarecursively enumerable sets and their metadegrees, this Journal, vol. 33 (1968), pp. 389–411.Google Scholar
[2]Friedberg, R. M., Three theorems on recursive enumeration, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[3]Kreisel, G. and Sacks, G. E., Metarecursive sets, this Journal, vol. 30 (1965), pp. 318–338.Google Scholar
[4]Owings, J. C. Jr., Topics in metacursion theory, Ph.D. thesis, Cornell University, 1966.Google Scholar
[5]Owings, J. G. Jr., Π11 sets, ω-sets, and metacompleteness, this Journal, vol. 34 (1969), pp. 194–204.Google Scholar
[6]Owings, J. C. Jr., The metarecursively enumerable sets but not the Π11 sets, can be enumerated without duplication, this Journal, vol. 35 (1970), pp. 223–229.Google Scholar
[7]Sacks, G. E., On the degrees less than O′, Annals of Mathematics, vol. 77 (1963), pp. 211–231.CrossRefGoogle Scholar
[8]Sacks, G. E., Metarecursion theory, Sets, models, and recursion theory, Leicester Symposium Volume, North-Holland, Amsterdam, 1965, pp. 243–263.Google Scholar