Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T19:00:54.331Z Has data issue: false hasContentIssue false
  • English
  • Français

SQUARES AND NARROW SYSTEMS

Published online by Cambridge University Press:  08 September 2017

CHRIS LAMBIE-HANSON
CHRIS LAMBIE-HANSON*
Affiliation:
DEPARTMENT OF MATHEMATICSBAR-ILAN UNIVERSITYRAMAT GAN 5290002, ISRAELE-mail: lambiec@macs.biu.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

A narrow system is a combinatorial object introduced by Magidor and Shelah in connection with work on the tree property at successors of singular cardinals. In analogy to the tree property, a cardinal κ satisfies the narrow system property if every narrow system of height κ has a cofinal branch. In this paper, we study connections between the narrow system property, square principles, and forcing axioms. We prove, assuming large cardinals, both that it is consistent that ℵω+1 satisfies the narrow system property and 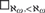$\square _{\aleph _\omega , < \aleph _\omega } $ holds and that it is consistent that every regular cardinal satisfies the narrow system property. We introduce natural strengthenings of classical square principles and show how they can be used to produce narrow systems with no cofinal branch. Finally, we show that the Proper Forcing Axiom implies that every narrow system of countable width has a cofinal branch but is consistent with the existence of a narrow system of width ω1 with no cofinal branch.

Keywords

Primary 03E35Secondary 03E0503E55tree propertynarrow systemssquare principleslarge cardinalsProper Forcing Axiom
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 3 , September 2017 , pp. 834 - 859
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Apter, A. W. and Cummings, J., A global version of a theorem of Ben-David and Magidor . Annals of Pure and Applied Logic, vol. 102 (2000), no. 3, pp. 199–222.Google Scholar
Cummings, J., Notes on singular cardinal combinatorics. Notre Dame Journal of Formal Logic, vol. 46 (2005), no. 3, pp. 251–282.Google Scholar
Cummings, J., Foreman, M., and Magidor, M., Squares, scales and stationary reflection . Journal of Mathematical Logic, vol. 1 (2001), no. 1, pp. 35–98.Google Scholar
Cummings, J. and Schimmerling, E., Indexed squares . Israel Journal of Mathematics, vol. 131 (2002), pp. 61–99.CrossRefGoogle Scholar
Eisworth, T., Successors of singular cardinals , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 1229–1350.Google Scholar
Fontanella, L. and Magidor, M., Reflection of stationary sets and the tree property at the successor of a singular cardinal, this JOURNAL, vol. 82 (2017), no. 1, pp. 272–291.Google Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Lambie-Hanson, C., Squares and covering matrices . Annals of Pure and Applied Logic, vol. 165 (2014), no. 2, pp. 673–694.Google Scholar
Laver, R., Making the supercompactness of κ indestructible under κ-directed closed forcing . Israel Journal of Mathematics, vol. 29 (1978), no. 4, pp. 385–388.CrossRefGoogle Scholar
Lévy, A. and Solovay, R. M., Measurable cardinals and the continuum hypothesis . Israel Journal of Mathematics, vol. 5 (1967), no. 4, pp. 234–248.Google Scholar
Magidor, M., Reflecting stationary sets , this JOURNAL, vol. 47 (1982), no. 4, pp. 755–771.Google Scholar
Magidor, M. and Shelah, S., The tree property at successors of singular cardinals . Archive for Mathematical Logic, vol. 35 (1996), no. 5–6, pp. 385–404.CrossRefGoogle Scholar
Neeman, I., The tree property up to ℵ ω+1, this JOURNAL, vol. 79 (2014), no. 2, pp. 429–459.Google Scholar
Shelah, S., On successors of singular cardinals , Logic Colloquium ’78 (Mons, 1978) (Boffa, M., van Dalen, D., and McAloon, K., editors), Studies in Logic and the Foundations of Mathematics, vol. 97, North-Holland, Amsterdam-New York, 1979, pp. 357–380.Google Scholar
Sinapova, D., The tree property at ℵ ω+1, this JOURNAL, vol. 77 (2012), no. 1, pp. 279–290.Google Scholar
Todorčević, S., Walks on Ordinals and their Characteristics, Progress in Mathematics, vol. 263, Birkhäuser Verlag, Basel, 2007.Google Scholar
Viale, M. and Weiss, C., On the consistency strength of the proper forcing axiom . Advances in Mathematics, vol. 228 (2011), no. 5, pp. 2672–2687.Google Scholar