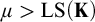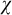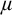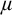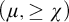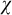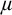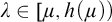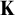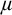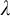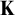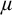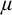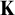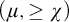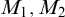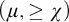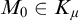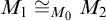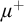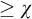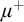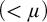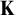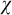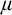1 Introduction
The notion of abstract elementary classes (AECs) was created by Shelah [Reference Shelah and Baldwin22] to encompass certain classes of models, including models of first-order theories. To develop the classification theory of AECs, notions like types, stability, and superstability were generalized to the AEC context. Superstability is a major topic in AECs because it is implied by categoricity and has good transfer properties (assuming tameness and a monster model). Early results could be found in [Reference Grossberg, VanDieren and Villaveces17, Reference Shelah23, Reference Shelah and Villaveces26–Reference VanDieren28], which were later extended by Boney, Grossberg, VanDieren, and Vasey.
Guided by the first-order case, Grossberg and Vasey [Reference Grossberg and Vasey18] provided several equivalent definitions of superstability for AECs: no long splitting chains, existence of a good frame, existence of a unique limit model, existence of a superlimit model, solvability, and that the union of an increasing chain of
![]() $\lambda $
-saturated models is
$\lambda $
-saturated models is
![]() $\lambda $
-saturated (where
$\lambda $
-saturated (where
![]() $\lambda $
is high enough). Later Vasey [Reference Vasey38, Corollary 4.24] added the (expected) criterion of stability in a tail. However, their results had two drawbacks:
$\lambda $
is high enough). Later Vasey [Reference Vasey38, Corollary 4.24] added the (expected) criterion of stability in a tail. However, their results had two drawbacks:
-
1. The cardinal threshold was high (the first Hanf number): if an AEC satisfies one of the criteria in
 $\operatorname {LS}(\mathbf {K})$
or
$\operatorname {LS}(\mathbf {K})$
or
 ${\operatorname {LS}(\mathbf {K})}^+$
, it does not necessarily imply any other criterion.
${\operatorname {LS}(\mathbf {K})}^+$
, it does not necessarily imply any other criterion. -
2. The cardinal jump was high between equivalent criteria: if an AEC satisfies one of the criteria in a (high-enough) cardinal
 $\lambda $
, it was only known that other criteria hold in a much bigger cardinal (sometimes
$\lambda $
, it was only known that other criteria hold in a much bigger cardinal (sometimes
 $\beth _\omega (\lambda )$
).
$\beth _\omega (\lambda )$
).
In this paper, we aim to refine the list of equivalent superstability criteria using known techniques in the literature. We reduce the cardinal threshold to
![]() ${\operatorname {LS}(\mathbf {K})}^+$
and the cardinal jump to a successor cardinal. The missing piece in [Reference Grossberg and Vasey18] was to show the uniqueness of limit models from no long splitting chains. The original approach used Galois-Morleyization and averages [Reference Boney and Vasey11] at the cost of a high cardinal jump. We observe that the tower approach from [Reference VanDieren and Vasey31] is cleaner and has no cardinal jump, which allows us to rewrite many results in the literature that involve the uniqueness of limit models.
${\operatorname {LS}(\mathbf {K})}^+$
and the cardinal jump to a successor cardinal. The missing piece in [Reference Grossberg and Vasey18] was to show the uniqueness of limit models from no long splitting chains. The original approach used Galois-Morleyization and averages [Reference Boney and Vasey11] at the cost of a high cardinal jump. We observe that the tower approach from [Reference VanDieren and Vasey31] is cleaner and has no cardinal jump, which allows us to rewrite many results in the literature that involve the uniqueness of limit models.
On the other hand, the equivalent criteria of superstability in first-order theories have their strictly-stable analogues. For example, when the local character of forking
![]() $\kappa (T)$
is uncountable, the union of an increasing chain of
$\kappa (T)$
is uncountable, the union of an increasing chain of
![]() $\lambda $
-saturated models is
$\lambda $
-saturated models is
![]() $\lambda $
-saturated, provided that the chain has cofinality at least
$\lambda $
-saturated, provided that the chain has cofinality at least
![]() $\kappa (T)$
. This motivates us to look for generalizations of the superstability criteria. It turns out that a key assumption is “continuity of nonsplitting,” which allows us to mimick the proofs of many superstable results. Such assumption was partially explored in [Reference Boney and VanDieren10, Reference Vasey38] but a full picture was yet to be seen. It seems that the study of stability is much more difficult without assuming continuity of nonsplitting: Vasey [Reference Vasey38] gave some eventual results of stability which were only applicable to high cardinals.
$\kappa (T)$
. This motivates us to look for generalizations of the superstability criteria. It turns out that a key assumption is “continuity of nonsplitting,” which allows us to mimick the proofs of many superstable results. Such assumption was partially explored in [Reference Boney and VanDieren10, Reference Vasey38] but a full picture was yet to be seen. It seems that the study of stability is much more difficult without assuming continuity of nonsplitting: Vasey [Reference Vasey38] gave some eventual results of stability which were only applicable to high cardinals.
In the following, we provide an overview of the upcoming sections and highlight some key theorems: Section 2 states the global assumptions and preliminaries. Section 3 studies the properties of nonsplitting, which will be used to build good frames in Section 4. The idea of good frames was developed in [Reference Shelah24, IV Theorem 4.10], assuming categoricity and non-ZFC axioms, in order to deduce nice structural properties of an AEC. Later Boney and Grossberg [Reference Boney and Grossberg6] built a good frame from coheir with the assumption of tameness and extension property of coheir in ZFC. Vasey [Reference Vasey34, Section 5] further developed on coheir and [Reference Vasey32] managed to construct a good frame at a high categoricity cardinal (categoricity can be replaced by superstability and type locality, but the initial cardinal of the good frame is still high).
Another approach to building a good frame is via nonsplitting. It is in general not clear whether uniqueness or transitivity hold for nonsplitting (where models are ordered by universal extensions). To resolve this problem, Vasey [Reference Vasey33] constructed nonforking from nonsplitting, which has nicer properties: assuming superstability in
![]() $K_{\mu }$
, tameness, and a monster model, nonforking gives rise to a good frame over the limit models in
$K_{\mu }$
, tameness, and a monster model, nonforking gives rise to a good frame over the limit models in
![]() $K_{\mu ^+}$
[Reference VanDieren and Vasey31, Corollary 6.14]. Later it was found that uniqueness of nonforking also holds for limit models in
$K_{\mu ^+}$
[Reference VanDieren and Vasey31, Corollary 6.14]. Later it was found that uniqueness of nonforking also holds for limit models in
![]() $K_{\mu }$
[Reference Vasey35].
$K_{\mu }$
[Reference Vasey35].
We will generalize the nonforking results by replacing the superstability assumption by continuity of nonsplitting. A key observation is that the extension property of nonforking still holds if we have continuity of nonsplitting and stability. This allows us to replicate extension, uniqueness, and transitivity properties. Since the assumption of continuity of nonsplitting applies to universal extensions only, we only get continuity and local character for universal extensions. Hence we can build an approximation of a good frame which is over the skeleton (see Definition 2.4) of long enough limit models ordered by universal extensions. We state the known result and our result for comparison.
Theorem 1.1. Let
![]() $\mu \geq \operatorname {LS}(\mathbf {K})$
,
$\mu \geq \operatorname {LS}(\mathbf {K})$
,
![]() $\mathbf {K}$
have a monster model, be
$\mathbf {K}$
have a monster model, be
![]() $\mu $
-tame and stable in
$\mu $
-tame and stable in
![]() $\mu $
. Let
$\mu $
. Let
![]() $\chi $
be the local character of
$\chi $
be the local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
-
1. [Reference Vasey37, Corollary 13.16] If
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-superstable, then there exists a good frame over the skeleton of limit models in
$\mu $
-superstable, then there exists a good frame over the skeleton of limit models in
 $K_{\mu }$
ordered by
$K_{\mu }$
ordered by
 $\leq _u$
, except for symmetry.
$\leq _u$
, except for symmetry. -
2. (Corollary 4.13) If
 $\mu $
is regular and
$\mu $
is regular and
 $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
 $\mu $
-nonsplitting, then there exists a good
$\mu $
-nonsplitting, then there exists a good
 $\mu $
-frame over the skeleton of
$\mu $
-frame over the skeleton of
 $(\mu ,\geq \chi )$
-limit models ordered by
$(\mu ,\geq \chi )$
-limit models ordered by
 $\leq _u$
, except for symmetry. The local character is
$\leq _u$
, except for symmetry. The local character is
 $\chi $
in place of
$\chi $
in place of
 ${\aleph _0}$
.
${\aleph _0}$
.
In Section 5, we will deduce symmetry under extra stability assumptions. In Section 6, we will generalize known superstability results using the symmetry properties. Symmetry is an important property of a good frame that connects superstability and the uniqueness of limit models. To obtain symmetry for our frame, we look into the argument in [Reference VanDieren and Vasey31]. In [Reference VanDieren29, Reference VanDieren30], VanDieren defined a stronger version of symmetry called
![]() $\mu $
-symmetry and proved its equivalence with the continuity of reduced towers. VanDieren and Vasey [Reference VanDieren and Vasey31, Lemma 4.6] noticed that a weaker version of symmetry is sufficient in one direction and deduced the weaker version of symmetry via superstability. To generalize these arguments, we replace superstability by continuity of nonsplitting and stability in a range of cardinals (the range depends on the no order property of
$\mu $
-symmetry and proved its equivalence with the continuity of reduced towers. VanDieren and Vasey [Reference VanDieren and Vasey31, Lemma 4.6] noticed that a weaker version of symmetry is sufficient in one direction and deduced the weaker version of symmetry via superstability. To generalize these arguments, we replace superstability by continuity of nonsplitting and stability in a range of cardinals (the range depends on the no order property of
![]() $\mathbf {K}$
, see Proposition 5.9). Then we can obtain a local version of
$\mathbf {K}$
, see Proposition 5.9). Then we can obtain a local version of
![]() $\mu $
-symmetry, which implies symmetry of our frame for long enough limit models.
$\mu $
-symmetry, which implies symmetry of our frame for long enough limit models.
Theorem 1.2. Let
![]() $\mu \geq \operatorname {LS}(\mathbf {K})$
,
$\mu \geq \operatorname {LS}(\mathbf {K})$
,
![]() $\mathbf {K}$
be
$\mathbf {K}$
be
![]() $\mu $
-tame and stable in
$\mu $
-tame and stable in
![]() $\mu $
. Let
$\mu $
. Let
![]() $\chi $
be the local character of
$\chi $
be the local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
-
1. [Reference VanDieren and Vasey31, Corollary 6.9] If
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-superstable, then it has
$\mu $
-superstable, then it has
 $\mu $
-symmetry.
$\mu $
-symmetry. -
2. (Corollary 5.13) If
 $\mu $
is regular and
$\mu $
is regular and
 $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
 $\mu $
-nonsplitting. There is
$\mu $
-nonsplitting. There is
 $\lambda <h(\mu )$
such that if
$\lambda <h(\mu )$
such that if
 $\mathbf {K}$
is stable in every cardinal between
$\mathbf {K}$
is stable in every cardinal between
 $\mu $
and
$\mu $
and
 $\lambda $
, then
$\lambda $
, then
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $(\mu ,\chi )$
-symmetry.
$(\mu ,\chi )$
-symmetry.
The notions of continuity of nonsplitting and of local symmetry were already exploited in [Reference Boney and VanDieren10, Theorem 20] to obtain the uniqueness of long enough limit models (see Fact 6.1). They simply assumed the local symmetry while we used the argument in [Reference VanDieren and Vasey31] to deduce it from extra stability and continuity of nonsplitting (Corollary 6.2). On the other hand, [Reference Vasey38, Section 11] used continuity of nonsplitting to deduce that a long enough chain of saturated models of the same cardinality is saturated. There he assumed saturation of limit models and managed to satisfy this assumption using his earlier result with Boney [Reference Boney and Vasey11], which has a high cardinal threshold. Since we already have local symmetry under continuity of nonsplitting and extra stability, we immediately have uniqueness of long limit models, and hence Vasey’s argument can be applied to obtain the above result of saturated models (see Proposition 6.6; a comparison table of the approaches can be found in Remark 6.8(2)).
Vasey [Reference Vasey38, Lemma 11.6] observed that a localization of VanDieren’s result [Reference VanDieren29] can give: if the union of a long enough chain of
![]() $\mu ^+$
-saturated models is
$\mu ^+$
-saturated models is
![]() $\mu ^+$
-saturated, then local symmetry is satisfied. Assuming more tameness, we use this observation to obtain converses of our results (see Main Theorem 8.1(4)
$\mu ^+$
-saturated, then local symmetry is satisfied. Assuming more tameness, we use this observation to obtain converses of our results (see Main Theorem 8.1(4)
![]() $\Rightarrow $
(3)). In particular, local symmetry will lead to uniqueness of long limit models, which implies local character of nonsplitting (Main Theorem 8.1(3)
$\Rightarrow $
(3)). In particular, local symmetry will lead to uniqueness of long limit models, which implies local character of nonsplitting (Main Theorem 8.1(3)
![]() $\Rightarrow $
(1)). Despite the important observation by Vasey, he did not derive these implications.
$\Rightarrow $
(1)). Despite the important observation by Vasey, he did not derive these implications.
Theorem 1.3. Let
![]() $\mu>\operatorname {LS}(\mathbf {K})$
,
$\mu>\operatorname {LS}(\mathbf {K})$
,
![]() $\delta \leq \mu $
be regular,
$\delta \leq \mu $
be regular,
![]() $\mathbf {K}$
have a monster model, be
$\mathbf {K}$
have a monster model, be
![]() $(<\mu )$
-tame, stable in
$(<\mu )$
-tame, stable in
![]() $\mu $
and has continuity of
$\mu $
and has continuity of
![]() $\mu $
-nonsplitting. If any increasing chain of
$\mu $
-nonsplitting. If any increasing chain of
![]() $\mu ^+$
-saturated models of cofinality
$\mu ^+$
-saturated models of cofinality
![]() $\geq \delta $
has a
$\geq \delta $
has a
![]() $\mu ^+$
-saturated union, then
$\mu ^+$
-saturated union, then
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $\delta $
-local character of
$\delta $
-local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
In the original list inside [Reference Grossberg and Vasey18],
![]() $(\lambda ,\xi )$
-solvability was considered for
$(\lambda ,\xi )$
-solvability was considered for
![]() $\lambda>\xi $
, which they showed to be an equivalent definition of superstability, with a huge jump of cardinal from no long splitting chains to solvability. Further developments in [Reference Vasey36] indicate that such solvability has downward transfer properties which seems too strong to be called superstability. We propose a variation where
$\lambda>\xi $
, which they showed to be an equivalent definition of superstability, with a huge jump of cardinal from no long splitting chains to solvability. Further developments in [Reference Vasey36] indicate that such solvability has downward transfer properties which seems too strong to be called superstability. We propose a variation where
![]() $\lambda =\xi $
and will prove its equivalence with no long splitting chains in the same cardinal above
$\lambda =\xi $
and will prove its equivalence with no long splitting chains in the same cardinal above
![]() $\mu ^+$
(under continuity of nonsplitting and stability). At
$\mu ^+$
(under continuity of nonsplitting and stability). At
![]() $K_{\mu }$
, we demand
$K_{\mu }$
, we demand
![]() $(<\mu )$
-tameness for the equivalence to hold, up to a jump to the successor cardinal.
$(<\mu )$
-tameness for the equivalence to hold, up to a jump to the successor cardinal.
Theorem 1.4. Let
![]() $\mu>\operatorname {LS}(\mathbf {K})$
,
$\mu>\operatorname {LS}(\mathbf {K})$
,
![]() $\mathbf {K}$
have a monster model, be
$\mathbf {K}$
have a monster model, be
![]() $(<\mu )$
-tame, stable in
$(<\mu )$
-tame, stable in
![]() $\mu $
.
$\mu $
.
-
1. [Reference Shelah and Villaveces26] If there is
 $\lambda>\mu $
such that
$\lambda>\mu $
such that
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(\lambda ,\mu )$
-solvable, then it is
$(\lambda ,\mu )$
-solvable, then it is
 $\mu $
-superstable.
$\mu $
-superstable. -
2. [Reference Grossberg and Vasey18, Corollary 5.5] If
 $\mu $
is high enough and
$\mu $
is high enough and
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-superstable, then there is some
$\mu $
-superstable, then there is some
 $\lambda \geq \mu $
and some
$\lambda \geq \mu $
and some
 $\lambda '<\lambda $
such that
$\lambda '<\lambda $
such that
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(\lambda ,\lambda ')$
-solvable.
$(\lambda ,\lambda ')$
-solvable. -
3. (Proposition 6.24) If
 $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
 $\mu $
-nonsplitting, then it is
$\mu $
-nonsplitting, then it is
 $\mu $
-superstable iff it is
$\mu $
-superstable iff it is
 $(\mu ^+,\mu ^+)$
-solvable.
$(\mu ^+,\mu ^+)$
-solvable.
In Section 7, we will consider two characterizations of superstability: stability in a tail and the boundedness of the U-rank. Vasey [Reference Vasey38, Corollary 4.24] showed that stability in a tail is also an equivalent definition of superstability, but the starting cardinal of superstability
![]() $(\lambda '(\mathbf {K}))^++\chi _1$
is only bounded above by the Hanf number of
$(\lambda '(\mathbf {K}))^++\chi _1$
is only bounded above by the Hanf number of
![]() $\mu $
(he also implicitly assumed continuity of nonsplitting in deriving his results). In contrast, we carry out a slightly different proof to obtain
$\mu $
(he also implicitly assumed continuity of nonsplitting in deriving his results). In contrast, we carry out a slightly different proof to obtain
![]() $\mu ^{ }$
-superstability, assuming stability in unboundedly many cardinals below
$\mu ^{ }$
-superstability, assuming stability in unboundedly many cardinals below
![]() $\mu ^{ }$
, and enough stability above
$\mu ^{ }$
, and enough stability above
![]() $\mu $
.
$\mu $
.
Theorem 1.5. Let
![]() $\mu>\operatorname {LS}(\mathbf {K})$
with cofinality
$\mu>\operatorname {LS}(\mathbf {K})$
with cofinality
![]() ${\aleph _0}$
,
${\aleph _0}$
,
![]() $\mathbf {K}$
have a monster model, have continuity of nonsplitting, be
$\mathbf {K}$
have a monster model, have continuity of nonsplitting, be
![]() $\mu $
-tame, stable in both
$\mu $
-tame, stable in both
![]() $\mu $
and unboundedly many cardinals below
$\mu $
and unboundedly many cardinals below
![]() $\mu $
.
$\mu $
.
-
1. [Reference Vasey38, Corollary 4.14] If
 $\mu \geq (\lambda '(\mathbf {K}))^++\chi _1$
, then
$\mu \geq (\lambda '(\mathbf {K}))^++\chi _1$
, then
 $ \mathbf {K}$
is
$ \mathbf {K}$
is
 $\mu $
-superstable.
$\mu $
-superstable. -
2. (Proposition 7.5) There is
 $\lambda <h(\mu )$
such that if
$\lambda <h(\mu )$
such that if
 $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
 $[\mu ,\lambda )$
, then it is
$[\mu ,\lambda )$
, then it is
 $\mu $
-superstable.
$\mu $
-superstable.
It was mentioned at the end of [Reference Grossberg and Vasey18] that the no tree property and the boundedness of a rank function could be generalized to AECs. Some partial answers were given in [Reference Grossberg and Mazari-Armida15] regarding the no tree property (assuming a simple independence relation). Here we prove that the boundedness of the U-rank (with respect to
![]() $\mu $
-nonforking for limit models in
$\mu $
-nonforking for limit models in
![]() $K_{\mu }$
ordered by universal extensions) is equivalent to
$K_{\mu }$
ordered by universal extensions) is equivalent to
![]() $\mu $
-superstability (Corollary 7.14). We will need to extend our nonforking to longer types, using results from [Reference Boney and Vasey12]. Then we can quote a lot of known results from [Reference Boney and Grossberg6, Reference Boney, Grossberg, Kolesnikov and Vasey7, Reference Grossberg and Mazari-Armida15]. Our strategy of extending frames contrasts with [Reference Vasey32] which used a complicated axiomatic framework and drew technical results from [Reference Shelah24, III]. Here we directly construct a type-full good
$\mu $
-superstability (Corollary 7.14). We will need to extend our nonforking to longer types, using results from [Reference Boney and Vasey12]. Then we can quote a lot of known results from [Reference Boney and Grossberg6, Reference Boney, Grossberg, Kolesnikov and Vasey7, Reference Grossberg and Mazari-Armida15]. Our strategy of extending frames contrasts with [Reference Vasey32] which used a complicated axiomatic framework and drew technical results from [Reference Shelah24, III]. Here we directly construct a type-full good
![]() $\mu $
-frame from nonforking and the known results apply (which are independent of the technical ones in [Reference Shelah24, Reference Vasey32]).
$\mu $
-frame from nonforking and the known results apply (which are independent of the technical ones in [Reference Shelah24, Reference Vasey32]).
Theorem 1.6. Let
![]() $\mu \geq \operatorname {LS}(\mathbf {K})$
be regular,
$\mu \geq \operatorname {LS}(\mathbf {K})$
be regular,
![]() $\mathbf {K}$
have a monster model, be
$\mathbf {K}$
have a monster model, be
![]() $\mu $
-tame, stable in
$\mu $
-tame, stable in
![]() $\mu $
and have continuity of
$\mu $
and have continuity of
![]() $\mu $
-nonsplitting. Let
$\mu $
-nonsplitting. Let
![]() $U(\cdot )$
be the U-rank induced by
$U(\cdot )$
be the U-rank induced by
![]() $\mu $
-nonforking restricted to limit models in
$\mu $
-nonforking restricted to limit models in
![]() $K_{\mu }$
ordered by
$K_{\mu }$
ordered by
![]() $\leq _u$
. The following are equivalent:
$\leq _u$
. The following are equivalent:
-
1.
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-superstable.
$\mu $
-superstable. -
2.
 $U(p)<\infty $
for all
$U(p)<\infty $
for all
 $p\in \operatorname {gS}(M)$
and limit model
$p\in \operatorname {gS}(M)$
and limit model
 $M\in K_{\mu }$
.
$M\in K_{\mu }$
.
In Section 8, we summarize all our results as two main theorems: one for the superstable case and one for the strictly stable case. We give two applications in algebra: those results were known but here we only rely on model-theoretic techniques.
2 Preliminaries
Throughout this paper, we assume the following:
Assumption 2.1.
-
1.
 $\mathbf {K}$
is an AEC with
$\mathbf {K}$
is an AEC with
 $AP$
,
$AP$
,
 $JEP,$
and
$JEP,$
and
 $NMM$
.
$NMM$
. -
2.
 $\mathbf {K}$
is stable in some
$\mathbf {K}$
is stable in some
 $\mu \geq \operatorname {LS}(\mathbf {K})$
.
$\mu \geq \operatorname {LS}(\mathbf {K})$
. -
3.
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-tame.
$\mu $
-tame. -
4.
 $\mathbf {K}$
satisfies continuity of
$\mathbf {K}$
satisfies continuity of
 $\mu $
-nonsplitting (Definition 3.5).
$\mu $
-nonsplitting (Definition 3.5). -
5.
 $\chi \leq \mu $
where
$\chi \leq \mu $
where
 $\chi $
is the minimum local character cardinal of
$\chi $
is the minimum local character cardinal of
 $\mu $
-nonsplitting (see Definition 3.10).
$\mu $
-nonsplitting (see Definition 3.10).
![]() $AP$
stands for amalgamation property,
$AP$
stands for amalgamation property,
![]() $JEP$
for joint embedding property, and
$JEP$
for joint embedding property, and
![]() $NMM$
for no maximal model. They allow the construction of a monster model. Given a model
$NMM$
for no maximal model. They allow the construction of a monster model. Given a model
![]() $M\in K$
, we write
$M\in K$
, we write
![]() $\operatorname {gS}(M)$
the set of Galois types over M (the ambient model does not matter because of
$\operatorname {gS}(M)$
the set of Galois types over M (the ambient model does not matter because of
![]() $AP$
).
$AP$
).
Definition 2.2. Let
![]() $\lambda $
be an infinite cardinal.
$\lambda $
be an infinite cardinal.
-
1.
 $\alpha \geq 2$
be an ordinal,
$\alpha \geq 2$
be an ordinal,
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(<\alpha )$
-stable in
$(<\alpha )$
-stable in
 $\lambda $
if for any
$\lambda $
if for any
 $\Vert M \Vert =\lambda $
,
$\Vert M \Vert =\lambda $
,
 $|\operatorname {gS}^{<\alpha }(M)|\leq \lambda $
. We omit
$|\operatorname {gS}^{<\alpha }(M)|\leq \lambda $
. We omit
 $\alpha $
if
$\alpha $
if
 $\alpha =2$
.
$\alpha =2$
. -
2.
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\lambda $
-tame if for any
$\lambda $
-tame if for any
 $N\in K$
, any
$N\in K$
, any
 $p\neq q\in \operatorname {gS}(N)$
, there is
$p\neq q\in \operatorname {gS}(N)$
, there is
 $M\leq N$
of size
$M\leq N$
of size
 $\lambda $
such that
$\lambda $
such that
 $p\restriction M\neq q\restriction M$
.
$p\restriction M\neq q\restriction M$
.
Definition 2.3. Let
![]() $\lambda \geq \operatorname {LS}(\mathbf {K})$
be a cardinal and
$\lambda \geq \operatorname {LS}(\mathbf {K})$
be a cardinal and
![]() $\alpha ,\beta <\lambda ^+$
be regular. Let
$\alpha ,\beta <\lambda ^+$
be regular. Let
![]() $M\leq N$
and
$M\leq N$
and
![]() $\Vert M \Vert =\lambda $
.
$\Vert M \Vert =\lambda $
.
-
1. N is universal over M (
 $M<_uN$
) if
$M<_uN$
) if
 $M<N$
and for any
$M<N$
and for any
 $\Vert N' \Vert =\Vert N \Vert $
, there is
$\Vert N' \Vert =\Vert N \Vert $
, there is
 $f:N'\xrightarrow [M]{}N$
.
$f:N'\xrightarrow [M]{}N$
. -
2. N is
 $(\lambda ,\alpha )$
-limit over M if
$(\lambda ,\alpha )$
-limit over M if
 $\Vert N \Vert =\lambda $
and there exists
$\Vert N \Vert =\lambda $
and there exists
 $\langle M_i:i\leq \alpha \rangle \subseteq K_\lambda $
increasing and continuous such that
$\langle M_i:i\leq \alpha \rangle \subseteq K_\lambda $
increasing and continuous such that
 $M_0=M$
,
$M_0=M$
,
 $M_\alpha =N$
and
$M_\alpha =N$
and
 $M_{i+1}$
is universal over
$M_{i+1}$
is universal over
 $M_i$
for
$M_i$
for
 $i<\alpha $
. We call
$i<\alpha $
. We call
 $\alpha $
the length of N.
$\alpha $
the length of N. -
3. N is
 $(\lambda ,\alpha )$
-limit if there exists
$(\lambda ,\alpha )$
-limit if there exists
 $\Vert M' \Vert =\lambda $
such that N is
$\Vert M' \Vert =\lambda $
such that N is
 $(\lambda ,\alpha )$
-limit over
$(\lambda ,\alpha )$
-limit over
 $M'$
.
$M'$
. -
4. N is
 $(\lambda ,\geq \beta )$
-limit (over M) if there exists
$(\lambda ,\geq \beta )$
-limit (over M) if there exists
 $\alpha \geq \beta $
such that (2) (resp. (3)) holds.
$\alpha \geq \beta $
such that (2) (resp. (3)) holds. -
5. N is
 $(\lambda ,\lambda ^+)$
-limit (over M) if
$(\lambda ,\lambda ^+)$
-limit (over M) if
 $\Vert N \Vert =\lambda ^+$
and we replace
$\Vert N \Vert =\lambda ^+$
and we replace
 $\alpha $
by
$\alpha $
by
 $\lambda ^+$
in (2) (resp. (3)).
$\lambda ^+$
in (2) (resp. (3)). -
6. Let
 $\lambda _1\leq \lambda _2$
, then N is
$\lambda _1\leq \lambda _2$
, then N is
 $([\lambda _1,\lambda _2],\geq \beta )$
-limit (over M) if there exists
$([\lambda _1,\lambda _2],\geq \beta )$
-limit (over M) if there exists
 $\lambda \in [\lambda _1,\lambda _2]$
such that N is
$\lambda \in [\lambda _1,\lambda _2]$
such that N is
 $(\lambda ,\geq \beta )$
-limit (over M).
$(\lambda ,\geq \beta )$
-limit (over M). -
7. If
 $\lambda>\operatorname {LS}(\mathbf {K})$
, we say M is
$\lambda>\operatorname {LS}(\mathbf {K})$
, we say M is
 $\lambda $
-saturated if for any
$\lambda $
-saturated if for any
 $M'\leq M$
,
$M'\leq M$
,
 $\Vert M' \Vert <\lambda $
,
$\Vert M' \Vert <\lambda $
,
 $M\vDash \operatorname {gS}(M')$
.
$M\vDash \operatorname {gS}(M')$
. -
8. M is saturated if it is
 $\Vert M \Vert $
-saturated.
$\Vert M \Vert $
-saturated.
In general, we do not know limit models or saturated models are closed under chains, so they do not necessary form an AEC. We adapt [Reference Vasey32, Definition 5.3] to capture such behaviours.
Definition 2.4. An abstract class
![]() $\mathbf {K}_{\mathbf {1}}$
is a
$\mathbf {K}_{\mathbf {1}}$
is a
![]() $\mu $
-skeleton of
$\mu $
-skeleton of
![]() $\mathbf {K}$
if the following is satisfied:
$\mathbf {K}$
if the following is satisfied:
-
1.
 $\mathbf {K}_{\mathbf {1}}$
is a sub-AC of
$\mathbf {K}_{\mathbf {1}}$
is a sub-AC of
 $\mathbf {K}_{\boldsymbol {\mu }}$
:
$\mathbf {K}_{\boldsymbol {\mu }}$
:
 $K_1\subseteq K_{\mu }$
and for any
$K_1\subseteq K_{\mu }$
and for any
 $M,N\in K_1$
,
$M,N\in K_1$
,
 $M\leq _{\mathbf {K}_{\mathbf {1}}} N$
implies
$M\leq _{\mathbf {K}_{\mathbf {1}}} N$
implies
 $M\leq _{\mathbf {K}} N$
.
$M\leq _{\mathbf {K}} N$
. -
2. For any
 $M\in K_{\mu }$
, there is
$M\in K_{\mu }$
, there is
 $M'\in K_1$
such that
$M'\in K_1$
such that
 $M\leq _{\mathbf {K}} M'$
.
$M\leq _{\mathbf {K}} M'$
. -
3. Let
 $\alpha $
be an ordinal and
$\alpha $
be an ordinal and
 $\langle M_i:i<\alpha \rangle $
be
$\langle M_i:i<\alpha \rangle $
be
 $\leq _{\mathbf {K}}$
-increasing in
$\leq _{\mathbf {K}}$
-increasing in
 $K_1$
. There exists
$K_1$
. There exists
 $N\in K_1$
such that for all
$N\in K_1$
such that for all
 $i<\alpha $
,
$i<\alpha $
,
 $M_i\leq _{\mathbf {K}_{\mathbf {1}}} N$
(the original definition requires strict inequality but it is immaterial under
$M_i\leq _{\mathbf {K}_{\mathbf {1}}} N$
(the original definition requires strict inequality but it is immaterial under
 $NMM$
).
$NMM$
).
We say
![]() $\mathbf {K}_{\mathbf {1}}$
is a
$\mathbf {K}_{\mathbf {1}}$
is a
![]() $(\geq \mu )$
-skeleton of
$(\geq \mu )$
-skeleton of
![]() $\mathbf {K}$
if the above items hold for
$\mathbf {K}$
if the above items hold for
![]() $K_{\geq \mu }$
in place of
$K_{\geq \mu }$
in place of
![]() $K_{\mu }$
.
$K_{\mu }$
.
By [Reference Shelah24, II Claim 1.16], limit models in
![]() $\mu $
with
$\mu $
with
![]() $\leq _{\mathbf {K}}$
form a
$\leq _{\mathbf {K}}$
form a
![]() $\mu $
-skeleton of
$\mu $
-skeleton of
![]() $\mathbf {K}$
. Similarly let
$\mathbf {K}$
. Similarly let
![]() $\alpha <\mu ^+$
be regular, then
$\alpha <\mu ^+$
be regular, then
![]() $(\geq \mu ,\geq \alpha )$
-limits form a
$(\geq \mu ,\geq \alpha )$
-limits form a
![]() $(\geq \mu )$
-skeleton of
$(\geq \mu )$
-skeleton of
![]() $\mathbf {K}$
.
$\mathbf {K}$
.
On the other hand, good frames were developed by Shelah [Reference Shelah24] for AECs in a range of cardinals. Vasey [Reference Vasey32] defined good frames over a coherent abstract class. We specialize the abstract class to a skeleton of an AEC.
Definition 2.5. Let
![]() $\mathbf {K}$
be an AEC, and let
$\mathbf {K}$
be an AEC, and let
![]() $\mathbf {K}_{\mathbf {1}}$
be a
$\mathbf {K}_{\mathbf {1}}$
be a
![]() $\mu $
-skeleton of
$\mu $
-skeleton of
![]() $\mathbf {K}$
. We say a nonforking relation is a good
$\mathbf {K}$
. We say a nonforking relation is a good
![]() $\mu $
-frame over the skeleton of
$\mu $
-frame over the skeleton of
![]() $\mathbf {K}_{\mathbf {1}}$
if the following holds:
$\mathbf {K}_{\mathbf {1}}$
if the following holds:
-
1. The nonforking relation is a binary relation between a type
 $p\in \operatorname {gS}(N)$
and a model
$p\in \operatorname {gS}(N)$
and a model
 $M\leq _{\mathbf {K}_{\mathbf {1}}}N$
. We say p does not fork over M if the relation holds between p and M. Otherwise we say p forks over M.
$M\leq _{\mathbf {K}_{\mathbf {1}}}N$
. We say p does not fork over M if the relation holds between p and M. Otherwise we say p forks over M. -
2. Invariance: if
 $f\in \operatorname {Aut}(\mathfrak {C})$
and p does not fork over M, then
$f\in \operatorname {Aut}(\mathfrak {C})$
and p does not fork over M, then
 $f(p)$
does not fork over
$f(p)$
does not fork over
 $f[M]$
.
$f[M]$
. -
3. Monotonicity: if
 $p\in \operatorname {gS}(N)$
does not fork over M and
$p\in \operatorname {gS}(N)$
does not fork over M and
 $M\leq _{\mathbf {K}_{\mathbf {1}}}M'\leq _{\mathbf {K}_{\mathbf {1}}} N$
for some
$M\leq _{\mathbf {K}_{\mathbf {1}}}M'\leq _{\mathbf {K}_{\mathbf {1}}} N$
for some
 $M'\in K_1$
, then
$M'\in K_1$
, then
 $p\restriction M'$
does not fork over M while p itself does not fork over
$p\restriction M'$
does not fork over M while p itself does not fork over
 $M'$
.
$M'$
. -
4. Existence: if
 $M\in K_1$
and
$M\in K_1$
and
 $p\in \operatorname {gS}(M)$
, then p does not fork over M.
$p\in \operatorname {gS}(M)$
, then p does not fork over M. -
5. Extension: if
 $M\leq _{\mathbf {K}_{\mathbf {1}}}N\leq _{\mathbf {K}_{\mathbf {1}}}N'$
and
$M\leq _{\mathbf {K}_{\mathbf {1}}}N\leq _{\mathbf {K}_{\mathbf {1}}}N'$
and
 $p\in \operatorname {gS}(N)$
does not fork over M, then there is
$p\in \operatorname {gS}(N)$
does not fork over M, then there is
 $q\in \operatorname {gS}(N')$
such that
$q\in \operatorname {gS}(N')$
such that
 $q\supseteq p$
and q does not fork over M.
$q\supseteq p$
and q does not fork over M. -
6. Uniqueness: if
 $p,q\in \operatorname {gS}(N)$
do not fork over M and
$p,q\in \operatorname {gS}(N)$
do not fork over M and
 $p\restriction M=q\restriction M$
, then
$p\restriction M=q\restriction M$
, then
 $p=q$
.
$p=q$
. -
7. Transitivity: if
 $M_0\leq _{\mathbf {K}_{\mathbf {1}}}M_1\leq _{\mathbf {K}_{\mathbf {1}}}M_2$
,
$M_0\leq _{\mathbf {K}_{\mathbf {1}}}M_1\leq _{\mathbf {K}_{\mathbf {1}}}M_2$
,
 $p\in \operatorname {gS}(M_2)$
does not fork over
$p\in \operatorname {gS}(M_2)$
does not fork over
 $M_1$
,
$M_1$
,
 $p\restriction M_1$
does not fork over
$p\restriction M_1$
does not fork over
 $M_0$
, then p does not fork over
$M_0$
, then p does not fork over
 $M_0$
.
$M_0$
. -
8. Local character
 ${\aleph _0}$
: if
${\aleph _0}$
: if
 $\delta $
is an ordinal of cofinality
$\delta $
is an ordinal of cofinality
 $\geq {\aleph _0}$
,
$\geq {\aleph _0}$
,
 $\langle M_i:i\leq \delta \rangle $
is
$\langle M_i:i\leq \delta \rangle $
is
 $\leq _{\mathbf {K}_{\mathbf {1}}}$
-increasing and continuous, then there is
$\leq _{\mathbf {K}_{\mathbf {1}}}$
-increasing and continuous, then there is
 $i<\delta $
such that p does not fork over
$i<\delta $
such that p does not fork over
 $M_i$
.
$M_i$
. -
9. Continuity: Let
 $\delta $
is a limit ordinal and
$\delta $
is a limit ordinal and
 $\langle M_i:i\leq \delta \rangle $
be
$\langle M_i:i\leq \delta \rangle $
be
 $\leq _{\mathbf {K}_{\mathbf {1}}}$
-increasing and continuous. If for all
$\leq _{\mathbf {K}_{\mathbf {1}}}$
-increasing and continuous. If for all
 $1\leq i<\delta $
,
$1\leq i<\delta $
,
 $p_i\in \operatorname {gS}(M_i)$
does not fork over
$p_i\in \operatorname {gS}(M_i)$
does not fork over
 $M_0$
and
$M_0$
and
 $p_{i+1}\supseteq p_i$
, then
$p_{i+1}\supseteq p_i$
, then
 $p_\delta $
does not fork over
$p_\delta $
does not fork over
 $M_0$
.
$M_0$
. -
10. Symmetry: let
 $M\leq _{\mathbf {K}_{\mathbf {1}}}N$
,
$M\leq _{\mathbf {K}_{\mathbf {1}}}N$
,
 $b\in |N|$
,
$b\in |N|$
,
 $\operatorname {gtp}(b/M)$
do not fork over M,
$\operatorname {gtp}(b/M)$
do not fork over M,
 $\operatorname {gtp}(a/N)$
do not fork over M. There is
$\operatorname {gtp}(a/N)$
do not fork over M. There is
 $N_a\geq _{\mathbf {K}_{\mathbf {1}}}M$
such that
$N_a\geq _{\mathbf {K}_{\mathbf {1}}}M$
such that
 $\operatorname {gtp}(b/N_a)$
do not fork over M.
$\operatorname {gtp}(b/N_a)$
do not fork over M.
If the above holds for a
![]() $(\geq \mu )$
-skeleton
$(\geq \mu )$
-skeleton
![]() $\mathbf {K}_{\mathbf {1}}$
, then we say the nonforking relation is a good
$\mathbf {K}_{\mathbf {1}}$
, then we say the nonforking relation is a good
![]() $(\geq \mu )$
-frame over the skeleton
$(\geq \mu )$
-frame over the skeleton
![]() $\mathbf {K}_{\mathbf {1}}$
. If
$\mathbf {K}_{\mathbf {1}}$
. If
![]() $\mathbf {K}_{\mathbf {1}}$
is itself an AEC (in
$\mathbf {K}_{\mathbf {1}}$
is itself an AEC (in
![]() $\mu $
), then we omit “skeleton.” Let
$\mu $
), then we omit “skeleton.” Let
![]() $\alpha <\mu ^+$
be regular. We say a nonforking relation has local character
$\alpha <\mu ^+$
be regular. We say a nonforking relation has local character
![]() $\alpha $
if we replace “
$\alpha $
if we replace “
![]() ${\aleph _0}$
” in item (8) by
${\aleph _0}$
” in item (8) by
![]() $\alpha $
.
$\alpha $
.
Remark 2.6.
-
1. In this paper,
 $\mathbf {K}_{\mathbf {1}}$
will be the
$\mathbf {K}_{\mathbf {1}}$
will be the
 $(\mu ,\geq \alpha )$
-limit models for some
$(\mu ,\geq \alpha )$
-limit models for some
 $\alpha <\mu ^+$
, with
$\alpha <\mu ^+$
, with
 $\leq _{\mathbf {K}_{\mathbf {1}}}=\leq _u$
(the latter is in
$\leq _{\mathbf {K}_{\mathbf {1}}}=\leq _u$
(the latter is in
 $\mathbf {K})$
.
$\mathbf {K})$
. -
2. In Fact 7.20, we will draw results of a good frame over longer types, where we allow the types in the above definition to be of arbitrary length. Extension property will have an extra clause that allows extension of a shorter type to a longer one that still does not fork over the same base.
-
3. Some of the properties of a good frame imply or simply one another. Instead of using a minimalistic formulation (for example, in [Reference Vasey37, Definition 17.1]), we keep all the properties because sometimes it is easier to deduce a certain property first.
3 Properties of nonsplitting
Let
![]() $p\in \operatorname {gS}(N)$
,
$p\in \operatorname {gS}(N)$
,
![]() $f:N\rightarrow N'$
, we write
$f:N\rightarrow N'$
, we write
![]() $f(p):=\operatorname {gtp}(f^+(d)/f(N))$
where
$f(p):=\operatorname {gtp}(f^+(d)/f(N))$
where
![]() $f^+$
extends f to include some
$f^+$
extends f to include some
![]() $d\vDash p$
in its domain.
$d\vDash p$
in its domain.
Proposition 3.1. Such
![]() $f^+$
exists by
$f^+$
exists by
![]() $AP$
and
$AP$
and
![]() $f(p)$
is independent of the choice of
$f(p)$
is independent of the choice of
![]() $f^+$
.
$f^+$
.
Proof Pick
![]() $a\in N_1\geq $
realizing p, use
$a\in N_1\geq $
realizing p, use
![]() $AP$
to obtain
$AP$
to obtain
![]() $f_1^+:a\mapsto c$
extending f (enlarge
$f_1^+:a\mapsto c$
extending f (enlarge
![]() $N_1$
if necessary so that
$N_1$
if necessary so that
![]() $f_1^+(N_1)$
contains
$f_1^+(N_1)$
contains
![]() $f(N)$
).
$f(N)$
).

Suppose
![]() $b\in N_2$
realizes p and there is
$b\in N_2$
realizes p and there is
![]() $f_2^+:b\mapsto d$
extending f. Extend
$f_2^+:b\mapsto d$
extending f. Extend
![]() $N_2$
so that
$N_2$
so that
![]() $f_2^+$
is an isomorphism. We need to find
$f_2^+$
is an isomorphism. We need to find
![]() $h:d\mapsto c$
which fixes
$h:d\mapsto c$
which fixes
![]() $f(N)$
. Since
$f(N)$
. Since
![]() $a,b\vDash p$
, by
$a,b\vDash p$
, by
![]() $AP$
there is
$AP$
there is
![]() $N_3\ni b$
and
$N_3\ni b$
and
![]() $g:N_1\xrightarrow [N]{}N_3$
that maps a to b. Extend g to an isomorphism
$g:N_1\xrightarrow [N]{}N_3$
that maps a to b. Extend g to an isomorphism
![]() $N_1'\cong _N N_3\geq N_2$
. By
$N_1'\cong _N N_3\geq N_2$
. By
![]() $AP$
again, obtain
$AP$
again, obtain
![]() $f_1^{++}$
of domain
$f_1^{++}$
of domain
![]() $N_1'$
extending
$N_1'$
extending
![]() $f_1^+$
. Therefore,
$f_1^+$
. Therefore,
![]() $d\in f(N_2^+)$
and
$d\in f(N_2^+)$
and
![]() $f_1^{++}\circ g^{-1}\circ \operatorname {id}_{N_2}\circ (f_2^+)^{-1}(d)=c$
. Hence we can take
$f_1^{++}\circ g^{-1}\circ \operatorname {id}_{N_2}\circ (f_2^+)^{-1}(d)=c$
. Hence we can take
![]() $h:= f_1^{++}\circ g^{-1}\circ \operatorname {id}_{N_2}\circ (f_2^+)^{-1}:f_2^+(N_2)\xrightarrow [f(N)]{}f_1^{++}(N_1') $
.
$h:= f_1^{++}\circ g^{-1}\circ \operatorname {id}_{N_2}\circ (f_2^+)^{-1}:f_2^+(N_2)\xrightarrow [f(N)]{}f_1^{++}(N_1') $
.
Definition 3.2. Let
![]() $M,N\in K$
,
$M,N\in K$
,
![]() $p\in \operatorname {gS}(N)$
.
$p\in \operatorname {gS}(N)$
.
![]() $p \ \mu $
-splits over M if there exists
$p \ \mu $
-splits over M if there exists
![]() $N_1,N_2$
of size
$N_1,N_2$
of size
![]() $\mu $
such that
$\mu $
such that
![]() $M\leq N_1,N_2\leq N$
and
$M\leq N_1,N_2\leq N$
and
![]() $f:N_1\xrightarrow [M]{}N_2$
such that
$f:N_1\xrightarrow [M]{}N_2$
such that
![]() $f(p)\restriction N_2\neq p\restriction N_2$
.
$f(p)\restriction N_2\neq p\restriction N_2$
.
Proposition 3.3 (Monotonicity of nonsplitting).
Let
![]() $M,N\in K_{\mu }$
,
$M,N\in K_{\mu }$
,
![]() $p\in \operatorname {gS}(N)$
do not
$p\in \operatorname {gS}(N)$
do not
![]() $\mu $
-split over M. For any
$\mu $
-split over M. For any
![]() $M_1,N_1$
with
$M_1,N_1$
with
![]() $M\leq M_1\leq N_1\leq N$
, we have
$M\leq M_1\leq N_1\leq N$
, we have
![]() $p\restriction N_1$
does not
$p\restriction N_1$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_1$
.
$M_1$
.
Proposition 3.4. Let
![]() $M,N\in K$
,
$M,N\in K$
,
![]() $M\in K_{\mu }$
and
$M\in K_{\mu }$
and
![]() $p\in \operatorname {gS}(N)$
.
$p\in \operatorname {gS}(N)$
.
![]() $p \ 5\mu $
-splits over M iff
$p \ 5\mu $
-splits over M iff
![]() $p \ (\geq \mu )$
-splits over M (the witnesses
$p \ (\geq \mu )$
-splits over M (the witnesses
![]() $N_1,N_2$
can be in
$N_1,N_2$
can be in
![]() $K_{\geq \mu }$
).
$K_{\geq \mu }$
).
Proof We sketch the backward direction: pick
![]() $N_1,N_2\in K_{\geq \mu }$
witnessing
$N_1,N_2\in K_{\geq \mu }$
witnessing
![]() $p \ (\geq \mu )$
-splits over M. By
$p \ (\geq \mu )$
-splits over M. By
![]() $\mu $
-tameness and Löwenheim–Skolem axiom, we may assume
$\mu $
-tameness and Löwenheim–Skolem axiom, we may assume
![]() $N_1,N_2\in K_{\mu }$
.
$N_1,N_2\in K_{\mu }$
.
Definition 3.5. Let
![]() $\chi $
be a regular cardinal.
$\chi $
be a regular cardinal.
-
1. A chain
 $\langle M_i:i\leq \delta \rangle $
is u-increasing if
$\langle M_i:i\leq \delta \rangle $
is u-increasing if
 $M_{i+1}>_uM_i$
for all
$M_{i+1}>_uM_i$
for all
 $i<\delta $
.
$i<\delta $
. -
2.
 $\mathbf {K}$
satisfies continuity of
$\mathbf {K}$
satisfies continuity of
 $\mu $
-nonsplitting if for any limit ordinal
$\mu $
-nonsplitting if for any limit ordinal
 $\delta $
,
$\delta $
,
 $\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$
u-increasing and continuous,
$\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$
u-increasing and continuous,
 $p\in \operatorname {gS}(M_\delta )$
,
$p\in \operatorname {gS}(M_\delta )$
,  $$ \begin{align*} p\restriction M_i \text{ does not } \mu\text{-split over } M_0 \text{ for } i < \delta \Rightarrow p \text{ does not } \mu\text{-split over } M_0. \end{align*} $$
$$ \begin{align*} p\restriction M_i \text{ does not } \mu\text{-split over } M_0 \text{ for } i < \delta \Rightarrow p \text{ does not } \mu\text{-split over } M_0. \end{align*} $$
-
3.
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\chi $
-weak local character of
$\chi $
-weak local character of
 $\mu $
-nonsplitting if for any limit ordinal
$\mu $
-nonsplitting if for any limit ordinal
 $\delta \geq \chi $
,
$\delta \geq \chi $
,
 $\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$
u-increasing and continuous,
$\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$
u-increasing and continuous,
 $p\in \operatorname {gS}(M_\delta )$
, there is
$p\in \operatorname {gS}(M_\delta )$
, there is
 $i<\delta $
such that
$i<\delta $
such that
 $p\restriction M_{i+1}$
does not
$p\restriction M_{i+1}$
does not
 $\mu $
-split over
$\mu $
-split over
 $M_i$
.
$M_i$
. -
4.
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\chi $
-local character of
$\chi $
-local character of
 $\mu $
-nonsplitting if the conclusion in (3) becomes: p does not
$\mu $
-nonsplitting if the conclusion in (3) becomes: p does not
 $\mu $
-split over
$\mu $
-split over
 $M_i$
.
$M_i$
.
We call any
![]() $\delta $
that satisfies (3) or (4) a (weak) local character cardinal.
$\delta $
that satisfies (3) or (4) a (weak) local character cardinal.
Remark 3.6. When defining the continuity of nonsplitting, we can weaken the statement by removing the assumption that p exists and replacing
![]() $p\restriction M_i$
by
$p\restriction M_i$
by
![]() $p_i$
increasing. This is because we can use [Reference Boney4, Proposition 5.2] to recover p. In details, we can use the weaker version of continuity and weak uniqueness (Proposition 3.12) to argue that the
$p_i$
increasing. This is because we can use [Reference Boney4, Proposition 5.2] to recover p. In details, we can use the weaker version of continuity and weak uniqueness (Proposition 3.12) to argue that the
![]() $p_i$
’s form a coherent sequence. p can be defined as the direct limit of the
$p_i$
’s form a coherent sequence. p can be defined as the direct limit of the
![]() $p_i$
’s.
$p_i$
’s.
The following lemma connects the three properties of
![]() $\mu $
-nonsplitting:
$\mu $
-nonsplitting:
Lemma 3.7 [Reference Boney, Grossberg, VanDieren and Vasey9, Lemma 11(1)].
If
![]() $\mu $
is regular,
$\mu $
is regular,
![]() $\mathbf {K}$
satisfies continuity of
$\mathbf {K}$
satisfies continuity of
![]() $\mu $
-nonsplitting and has
$\mu $
-nonsplitting and has
![]() $\chi $
-weak local character of
$\chi $
-weak local character of
![]() $\mu $
-nonsplitting, then it has
$\mu $
-nonsplitting, then it has
![]() $\chi $
-local character of
$\chi $
-local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
Proof Let
![]() $\delta $
be a limit ordinal of cofinality
$\delta $
be a limit ordinal of cofinality
![]() $\geq \chi $
,
$\geq \chi $
,
![]() $\langle M_i:i\leq \delta \rangle $
u-increasing and continuous. Suppose
$\langle M_i:i\leq \delta \rangle $
u-increasing and continuous. Suppose
![]() $p\in \operatorname {gS}(M_\delta )$
splits over
$p\in \operatorname {gS}(M_\delta )$
splits over
![]() $M_i$
for all
$M_i$
for all
![]() $i<\delta $
. Define
$i<\delta $
. Define
![]() $i_0:=0$
. By
$i_0:=0$
. By
![]() $\delta $
regular and continuity of
$\delta $
regular and continuity of
![]() $\mu $
-nonsplitting, build an increasing and continuous sequence of indices
$\mu $
-nonsplitting, build an increasing and continuous sequence of indices
![]() $\langle i_k:k<\delta \rangle $
such that
$\langle i_k:k<\delta \rangle $
such that
![]() $p\restriction M_{i_{k+1}} \ \mu $
-splits over
$p\restriction M_{i_{k+1}} \ \mu $
-splits over
![]() $M_{i_k}$
. Notice that
$M_{i_k}$
. Notice that
![]() $M_{i_{k+1}}>_uM_{i_k}$
. Then applying
$M_{i_{k+1}}>_uM_{i_k}$
. Then applying
![]() $\chi $
-weak local character to
$\chi $
-weak local character to
![]() $\langle M_{i_k}:k<\delta \rangle $
yields a contradiction.
$\langle M_{i_k}:k<\delta \rangle $
yields a contradiction.
From stability (even without continuity of nonsplitting), it is always possible to obtain weak local character of nonsplitting. Shelah sketched the proof and alluded to the first-order analog, so we give details here.
Lemma 3.8 [Reference Shelah23, Claim 3.3(2)].
If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $\mu $
(which is in Assumption 2.1), then for some
$\mu $
(which is in Assumption 2.1), then for some
![]() $\chi \leq \mu $
, it has weak
$\chi \leq \mu $
, it has weak
![]() $\chi $
-local character of
$\chi $
-local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
Proof Pick
![]() $\chi \leq \mu $
minimum such that
$\chi \leq \mu $
minimum such that
![]() $2^{\chi }>\mu $
. Suppose we have
$2^{\chi }>\mu $
. Suppose we have
![]() $\langle M_i:i\leq \chi \rangle $
u-increasing and continuous and
$\langle M_i:i\leq \chi \rangle $
u-increasing and continuous and
![]() $d\vDash p\in \operatorname {gS}(M_\chi )$
such that for all
$d\vDash p\in \operatorname {gS}(M_\chi )$
such that for all
![]() $i<\chi $
,
$i<\chi $
,
![]() $p\restriction M_{i+1} \ \mu $
-splits over
$p\restriction M_{i+1} \ \mu $
-splits over
![]() $p\restriction M_i$
. Then for
$p\restriction M_i$
. Then for
![]() $i<\chi $
, we have
$i<\chi $
, we have
![]() $N_i^1$
and
$N_i^1$
and
![]() $N_i^2$
of size
$N_i^2$
of size
![]() $\mu $
,
$\mu $
,
![]() $M_i\leq N_i^1,N_i^2\leq M_{i+1}$
,
$M_i\leq N_i^1,N_i^2\leq M_{i+1}$
,
![]() $f_i:N_i^1\cong _{M_i}N_i^2$
and
$f_i:N_i^1\cong _{M_i}N_i^2$
and
![]() $f_i(p)\restriction N_i^2\neq p\restriction N_i^2$
. We build
$f_i(p)\restriction N_i^2\neq p\restriction N_i^2$
. We build
![]() $\langle M_i':i\leq \chi \rangle $
and
$\langle M_i':i\leq \chi \rangle $
and
![]() $\langle h_\eta :M_{l(\eta )}\xrightarrow [M_0]{}M_{l(\eta )}'\,|\,\eta \in 2^{\leq \chi }\rangle $
both increasing and continuous with the following requirements:
$\langle h_\eta :M_{l(\eta )}\xrightarrow [M_0]{}M_{l(\eta )}'\,|\,\eta \in 2^{\leq \chi }\rangle $
both increasing and continuous with the following requirements:
-
1.
 $h_{\langle \rangle }:=\operatorname {id}_{M_0}$
and
$h_{\langle \rangle }:=\operatorname {id}_{M_0}$
and
 $M_0':= M_0$
.
$M_0':= M_0$
. -
2. For
 $\eta \in 2^{<\chi }$
,
$\eta \in 2^{<\chi }$
,
 $h_{\eta ^\frown 0}\restriction N_{l(\eta )}^2=h_{\eta ^\frown 1}\restriction N_{l(\eta )}^2$
.
$h_{\eta ^\frown 0}\restriction N_{l(\eta )}^2=h_{\eta ^\frown 1}\restriction N_{l(\eta )}^2$
.

We specify the successor step: suppose
![]() $l(\nu )=i$
and
$l(\nu )=i$
and
![]() $h_\nu $
has been constructed. By
$h_\nu $
has been constructed. By
![]() $AP$
, obtain:
$AP$
, obtain:
-
1.
 $h:N_i^2\rightarrow M^*\geq M_i'$
with
$h:N_i^2\rightarrow M^*\geq M_i'$
with
 $h\supseteq h_\nu $
.
$h\supseteq h_\nu $
. -
2.
 $h_{\nu ^\frown 0}:M_{i+1}\rightarrow M^{**}\geq M^*$
with
$h_{\nu ^\frown 0}:M_{i+1}\rightarrow M^{**}\geq M^*$
with
 $h_{\nu ^\frown 0}\supseteq h$
.
$h_{\nu ^\frown 0}\supseteq h$
. -
3.
 $g_0:M_{i+1}\rightarrow M_{hf_i}\geq M^*$
with
$g_0:M_{i+1}\rightarrow M_{hf_i}\geq M^*$
with
 $g_0\supseteq h\circ f_i$
.
$g_0\supseteq h\circ f_i$
. -
4.
 $g_1:M_{hf_i}\rightarrow M_{i+1}'\geq M^{**}$
with
$g_1:M_{hf_i}\rightarrow M_{i+1}'\geq M^{**}$
with
 $g_1\circ g_0=h_{\nu ^\frown 0}$
.
$g_1\circ g_0=h_{\nu ^\frown 0}$
.
Define
![]() $h_{\nu ^\frown 1}:= g_1\circ g_0:M_{i+1}\rightarrow M_{i+1}'$
. By diagram chasing,
$h_{\nu ^\frown 1}:= g_1\circ g_0:M_{i+1}\rightarrow M_{i+1}'$
. By diagram chasing,
![]() $h_{\nu ^\frown 1}\restriction M_i=g_1\circ g_0\restriction M_i=g_1\circ h\circ f_i\restriction M_i=g_1\circ h\restriction M_i=h\restriction M_i=h_\nu \restriction M_i$
. On the other hand,
$h_{\nu ^\frown 1}\restriction M_i=g_1\circ g_0\restriction M_i=g_1\circ h\circ f_i\restriction M_i=g_1\circ h\restriction M_i=h\restriction M_i=h_\nu \restriction M_i$
. On the other hand,
![]() $h_{\nu ^\frown 0}\restriction M_i=h\restriction M_i=h_\nu \restriction M_i$
. Therefore the maps are increasing. Now
$h_{\nu ^\frown 0}\restriction M_i=h\restriction M_i=h_\nu \restriction M_i$
. Therefore the maps are increasing. Now
![]() $h_{\nu ^\frown 1}\restriction N_i^2=g_1\circ g_0\restriction N_i^2=h_{\nu ^\frown 0}\restriction N_i^2$
by item (4) in our construction.
$h_{\nu ^\frown 1}\restriction N_i^2=g_1\circ g_0\restriction N_i^2=h_{\nu ^\frown 0}\restriction N_i^2$
by item (4) in our construction.
For
![]() $\eta \in 2^{\chi }$
, extend
$\eta \in 2^{\chi }$
, extend
![]() $h_\eta $
so that its range includes
$h_\eta $
so that its range includes
![]() $M_\chi '$
and its domain includes d. We show that
$M_\chi '$
and its domain includes d. We show that
![]() $\{\operatorname {gtp}(h_\eta (d)/M_{\chi }'):\eta \in 2^{\chi }\}$
are pairwise distinct. For any
$\{\operatorname {gtp}(h_\eta (d)/M_{\chi }'):\eta \in 2^{\chi }\}$
are pairwise distinct. For any
![]() $\eta \neq \nu \in 2^{\chi }$
, pick the minimum
$\eta \neq \nu \in 2^{\chi }$
, pick the minimum
![]() $i<\chi $
such that
$i<\chi $
such that
![]() $\eta [i]\neq \nu [i]$
. Without loss of generality, assume
$\eta [i]\neq \nu [i]$
. Without loss of generality, assume
![]() $\eta [i]=0$
,
$\eta [i]=0$
,
![]() $\nu [i]=1$
. Using the diagram above (see the comment before Proposition 3.1),
$\nu [i]=1$
. Using the diagram above (see the comment before Proposition 3.1),
 $$ \begin{align*} \operatorname{gtp}(h_\eta(d)/M_{\chi}')&\supseteq\operatorname{gtp}(h_{\eta}(d)/h(N_i^2))\\ &=h(\operatorname{gtp}(d/N_i^2))\\ &\neq h\circ f_i(\operatorname{gtp}(d/N_i^1))\\ &=g_1\circ h\circ f_i(\operatorname{gtp}(d/N_i^1))\\ &\subseteq\operatorname{gtp}(h_\nu(d)/M_{\chi}'). \end{align*} $$
$$ \begin{align*} \operatorname{gtp}(h_\eta(d)/M_{\chi}')&\supseteq\operatorname{gtp}(h_{\eta}(d)/h(N_i^2))\\ &=h(\operatorname{gtp}(d/N_i^2))\\ &\neq h\circ f_i(\operatorname{gtp}(d/N_i^1))\\ &=g_1\circ h\circ f_i(\operatorname{gtp}(d/N_i^1))\\ &\subseteq\operatorname{gtp}(h_\nu(d)/M_{\chi}'). \end{align*} $$
This contradicts the stability in
![]() $\mu $
.
$\mu $
.
Proposition 3.9. If
![]() $\mu $
is regular, then for some
$\mu $
is regular, then for some
![]() $\chi \leq \mu $
,
$\chi \leq \mu $
,
![]() $\mathbf {K}$
has the
$\mathbf {K}$
has the
![]() $\chi $
-local character of
$\chi $
-local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
Proof By Lemma 3.8 and uniqueness of limit models of the same cofinality,
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $\mu $
-weak local character of
$\mu $
-weak local character of
![]() $\mu $
-nonsplitting. By Lemma 3.7 (together with continuity of
$\mu $
-nonsplitting. By Lemma 3.7 (together with continuity of
![]() $\mu $
-nonsplitting in Assumption 2.1),
$\mu $
-nonsplitting in Assumption 2.1),
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $\mu $
-local character of
$\mu $
-local character of
![]() $\mu $
-nonsplitting. Hence
$\mu $
-nonsplitting. Hence
![]() $\chi $
exists and
$\chi $
exists and
![]() $\chi \leq \mu $
.
$\chi \leq \mu $
.
From now on, we fix the following.
Definition 3.10.
![]() $\chi $
is the minimum local character cardinal of
$\chi $
is the minimum local character cardinal of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
![]() $\chi \leq \mu $
if either
$\chi \leq \mu $
if either
![]() $\mu $
is regular (by the previous proposition), or
$\mu $
is regular (by the previous proposition), or
![]() $\mu $
is greater than some regular stability cardinal
$\mu $
is greater than some regular stability cardinal
![]() $\xi $
where
$\xi $
where
![]() $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
![]() $\xi $
-nonsplitting and is
$\xi $
-nonsplitting and is
![]() $\xi $
-tame (by Lemma 6.7).
$\xi $
-tame (by Lemma 6.7).
Remark 3.11. Without continuity of nonsplitting, it is not clear whether there can be gaps between the local character cardinals: Definition 3.5(4) might hold for
![]() $\delta =\aleph _0$
and
$\delta =\aleph _0$
and
![]() $\delta =\aleph _2$
but not
$\delta =\aleph _2$
but not
![]() $\delta =\aleph _1$
. In that case defining
$\delta =\aleph _1$
. In that case defining
![]() $\chi $
as the minimum local character cardinal might not be useful. Similar obstacles form when we only know a particular
$\chi $
as the minimum local character cardinal might not be useful. Similar obstacles form when we only know a particular
![]() $\lambda $
is a local character cardinal but not necessary those above
$\lambda $
is a local character cardinal but not necessary those above
![]() $\lambda $
.
$\lambda $
.
Meanwhile, weak local character cardinals close upwards and we can eliminate the above situation by assuming continuity of nonsplitting: if we know
![]() $\chi $
is the minimum local character cardinal, then it is also a weak local character cardinal, so are all regular cardinals between
$\chi $
is the minimum local character cardinal, then it is also a weak local character cardinal, so are all regular cardinals between
![]() $[\chi ,\mu ^+)$
. By the proof of Lemma 3.7, the regular cardinals between
$[\chi ,\mu ^+)$
. By the proof of Lemma 3.7, the regular cardinals between
![]() $[\chi ,\mu ^+)$
are all local character cardinals.
$[\chi ,\mu ^+)$
are all local character cardinals.
We now state the existence, extension, weak uniqueness, and weak transitivity properties of
![]() $\mu $
-nonsplitting. The original proof for weak uniqueness assumes
$\mu $
-nonsplitting. The original proof for weak uniqueness assumes
![]() $\Vert M \Vert =\mu $
but it is not necessary; while that for extension and for weak transitivity assume all models are in
$\Vert M \Vert =\mu $
but it is not necessary; while that for extension and for weak transitivity assume all models are in
![]() $K_{\mu }$
; but under tameness we can just require
$K_{\mu }$
; but under tameness we can just require
![]() $\Vert M \Vert =\Vert N \Vert $
.
$\Vert M \Vert =\Vert N \Vert $
.
Proposition 3.12. Let
![]() $M_0<_u M\leq N$
where
$M_0<_u M\leq N$
where
![]() $\Vert M_0 \Vert =\mu $
.
$\Vert M_0 \Vert =\mu $
.
-
1. [Reference Shelah23, Claim 3.3(1)] (Existence) If
 $p\in \operatorname {gS}(N)$
, there is
$p\in \operatorname {gS}(N)$
, there is
 $N_0\leq N$
of size
$N_0\leq N$
of size
 $\mu $
such that p does not
$\mu $
such that p does not
 $\mu $
-split over
$\mu $
-split over
 $N_0$
.
$N_0$
. -
2. [Reference Grossberg and VanDieren16, Theorem 6.2] (Weak uniqueness) If
 $p,q\in \operatorname {gS}(N)$
both do not
$p,q\in \operatorname {gS}(N)$
both do not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
, and
$M_0$
, and
 $p\restriction M=q\restriction M$
, then
$p\restriction M=q\restriction M$
, then
 $p=q$
.
$p=q$
. -
3. [Reference Grossberg and VanDieren16, Theorem 6.1] (Extension) Suppose
 $\Vert M \Vert =\Vert N \Vert $
. For any
$\Vert M \Vert =\Vert N \Vert $
. For any
 $p\in \operatorname {gS}(M)$
that does not
$p\in \operatorname {gS}(M)$
that does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
, there is
$M_0$
, there is
 $q\in \operatorname {gS}(N)$
extending p such that q does not
$q\in \operatorname {gS}(N)$
extending p such that q does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
.
$M_0$
. -
4. [Reference Vasey33, Proposition 3.7] (Weak transitivity) Suppose
 $\Vert M \Vert =\Vert N \Vert $
. Let
$\Vert M \Vert =\Vert N \Vert $
. Let
 $M^*\leq M_0$
and
$M^*\leq M_0$
and
 $p\in \operatorname {gS}(N)$
. If p does not
$p\in \operatorname {gS}(N)$
. If p does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
while
$M_0$
while
 $p\restriction M$
does not
$p\restriction M$
does not
 $\mu $
-split over
$\mu $
-split over
 $M^*$
, then p does not
$M^*$
, then p does not
 $\mu $
-split over
$\mu $
-split over
 $M^*$
.
$M^*$
.
Proof
-
1. We skip the proof, which has the same spirit as that of Lemma 3.8.
-
2. By stability in
 $\mu $
, we may assume that
$\mu $
, we may assume that
 $\Vert M \Vert =\mu $
. Suppose
$\Vert M \Vert =\mu $
. Suppose
 $p\neq q$
, by tameness in
$p\neq q$
, by tameness in
 $\mu $
we may find
$\mu $
we may find
 $M'\in K_{\mu }$
such that
$M'\in K_{\mu }$
such that
 $M\leq M'\leq N$
and
$M\leq M'\leq N$
and
 $p\restriction M'\neq q\restriction M'$
. By
$p\restriction M'\neq q\restriction M'$
. By
 $M_0<_uM$
and
$M_0<_uM$
and
 $M_0<N$
, we can find
$M_0<N$
, we can find
 $f:M'\xrightarrow [M_0]{}M$
. Using nonsplitting twice, we have
$f:M'\xrightarrow [M_0]{}M$
. Using nonsplitting twice, we have
 $p\restriction f(M')=f(p)$
and
$p\restriction f(M')=f(p)$
and
 $q\restriction M'=f(q)$
. But
$q\restriction M'=f(q)$
. But
 $f(M')\leq M$
implies
$f(M')\leq M$
implies
 $p\restriction f(M')=q\restriction f(M')$
. Hence
$p\restriction f(M')=q\restriction f(M')$
. Hence
 $f(p)=f(q)$
and
$f(p)=f(q)$
and
 $p=q$
.
$p=q$
. -
3. By universality of M, find
 $f:N\xrightarrow [M_0]{}M$
. We can set
$f:N\xrightarrow [M_0]{}M$
. We can set
 $q:= f^{-1}(p\restriction f(N))$
.
$q:= f^{-1}(p\restriction f(N))$
. -
4. Let
 $q:= p\restriction M$
. By extension, obtain
$q:= p\restriction M$
. By extension, obtain
 $q'\supseteq q$
in
$q'\supseteq q$
in
 $\operatorname {gS}(N)$
such that
$\operatorname {gS}(N)$
such that
 $q'$
does not
$q'$
does not
 $\mu $
-split over
$\mu $
-split over
 $M^*$
. Now
$M^*$
. Now
 $p\restriction M=q\restriction M=q'\restriction M$
and both
$p\restriction M=q\restriction M=q'\restriction M$
and both
 $p,q'$
do not
$p,q'$
do not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
(for
$M_0$
(for
 $q'$
use monotonicity, see Proposition 3.3). By weak uniqueness,
$q'$
use monotonicity, see Proposition 3.3). By weak uniqueness,
 $p=q'$
and the latter does not
$p=q'$
and the latter does not
 $\mu $
-split over
$\mu $
-split over
 $M^*$
.
$M^*$
.
Transitivity does not hold in general for
![]() $\mu $
-nonsplitting. The following example is sketched in [Reference Baldwin2, Example 19.3].
$\mu $
-nonsplitting. The following example is sketched in [Reference Baldwin2, Example 19.3].
Example 3.13. Let T be the first-order theory of a single equivalence relation E with infinitely many equivalence classes and each class is infinite. Let
![]() $M\leq N$
where N contains (representatives of) two more classes than M. Let d be an element. Then
$M\leq N$
where N contains (representatives of) two more classes than M. Let d be an element. Then
![]() $\operatorname {\mathrm {tp}}(d/N)$
splits over M iff
$\operatorname {\mathrm {tp}}(d/N)$
splits over M iff
![]() $dEa$
for some element
$dEa$
for some element
![]() $a\in N$
but
$a\in N$
but
![]() $\neg dEb$
for any
$\neg dEb$
for any
![]() $b\in M$
. Meanwhile, suppose
$b\in M$
. Meanwhile, suppose
![]() $M_0\leq M$
both of size
$M_0\leq M$
both of size
![]() $\mu $
, then
$\mu $
, then
![]() $M_0<_u M$
iff M contains
$M_0<_u M$
iff M contains
![]() $\mu $
-many new classes and each class extends
$\mu $
-many new classes and each class extends
![]() $\mu $
many elements. Now require
$\mu $
many elements. Now require
![]() $M_0<_u M$
while N contains only an extra class than M, say witnessed by d, then
$M_0<_u M$
while N contains only an extra class than M, say witnessed by d, then
![]() $\operatorname {\mathrm {tp}}(d/N)$
cannot split over M. Also
$\operatorname {\mathrm {tp}}(d/N)$
cannot split over M. Also
![]() $\operatorname {\mathrm {tp}}(d/M)$
does not split over
$\operatorname {\mathrm {tp}}(d/M)$
does not split over
![]() $M_0$
because d is not equivalent to any elements from M. Finally
$M_0$
because d is not equivalent to any elements from M. Finally
![]() $\operatorname {\mathrm {tp}}(d/N)$
splits over
$\operatorname {\mathrm {tp}}(d/N)$
splits over
![]() $M_0$
because it contains two more classes than
$M_0$
because it contains two more classes than
![]() $M_0$
(one must be from M).
$M_0$
(one must be from M).
The same argument does not work if also
![]() $M<_u N$
because N would contain two more classes than M and they will witness
$M<_u N$
because N would contain two more classes than M and they will witness
![]() $\operatorname {\mathrm {tp}}(d/N)$
splits over M. Baldwin originally assigned it as [Reference Baldwin2, Exercise 12.9] but later [Reference Baldwin3] retracted the claim.
$\operatorname {\mathrm {tp}}(d/N)$
splits over M. Baldwin originally assigned it as [Reference Baldwin2, Exercise 12.9] but later [Reference Baldwin3] retracted the claim.
Question 3.14. When models are ordered by
![]() $\leq _u$
:
$\leq _u$
:
-
1. Does uniqueness of
 $\mu $
-nonsplitting hold? Namely, let
$\mu $
-nonsplitting hold? Namely, let
 $M<_uN$
both in
$M<_uN$
both in
 $K_{\mu }$
,
$K_{\mu }$
,
 $p,q\in \operatorname {gS}(N)$
both do not
$p,q\in \operatorname {gS}(N)$
both do not
 $\mu $
-split over M,
$\mu $
-split over M,
 $p\restriction M=q\restriction M$
, then
$p\restriction M=q\restriction M$
, then
 $p=q$
.
$p=q$
. -
2. Does transitivity of
 $\mu $
-nonsplitting hold? Namely, let
$\mu $
-nonsplitting hold? Namely, let
 $M_0<_uM<_uN$
all in
$M_0<_uM<_uN$
all in
 $K_{\mu }$
,
$K_{\mu }$
,
 $p\in \operatorname {gS}(N)$
does not
$p\in \operatorname {gS}(N)$
does not
 $\mu $
-split over M and
$\mu $
-split over M and
 $p\restriction M$
does not
$p\restriction M$
does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
, then p does not
$M_0$
, then p does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
.
$M_0$
.
In Assumption 2.1, we assumed continuity of
![]() $\mu $
-nonsplitting. One way to obtain it is to assume superstability which is stronger. Another way is to assume
$\mu $
-nonsplitting. One way to obtain it is to assume superstability which is stronger. Another way is to assume
![]() $\omega $
-type locality.
$\omega $
-type locality.
Definition 3.15.
-
1. [Reference Grossberg and Zhang14, Definition 7.12] Let
 $\lambda \geq \operatorname {LS}(\mathbf {K})$
,
$\lambda \geq \operatorname {LS}(\mathbf {K})$
,
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\lambda $
-superstable if it is stable in
$\lambda $
-superstable if it is stable in
 $\lambda $
and has
$\lambda $
and has
 ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
 $\lambda $
-nonsplitting.
$\lambda $
-nonsplitting. -
2. [Reference Baldwin2, Definition 11.4] Types in
 $\mathbf {K}$
are
$\mathbf {K}$
are
 $\omega $
-local if: for any limit ordinal
$\omega $
-local if: for any limit ordinal
 $\alpha $
,
$\alpha $
,
 $\langle M_i:i\leq \alpha \rangle $
increasing and continuous,
$\langle M_i:i\leq \alpha \rangle $
increasing and continuous,
 $p,q\in \operatorname {gS}(M)$
and
$p,q\in \operatorname {gS}(M)$
and
 $p\restriction M_i=q\restriction M_i$
for all
$p\restriction M_i=q\restriction M_i$
for all
 $i<\alpha $
, then
$i<\alpha $
, then
 $p=q$
.
$p=q$
.
Proposition 3.16. Let
![]() $\mathbf {K}$
satisfy Assumption 2.1 except for the continuity of
$\mathbf {K}$
satisfy Assumption 2.1 except for the continuity of
![]() $\mu $
-nonsplitting. It will satisfy the continuity of
$\mu $
-nonsplitting. It will satisfy the continuity of
![]() $\mu $
-nonsplitting if either:
$\mu $
-nonsplitting if either:
-
1.
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-superstable; or
$\mu $
-superstable; or -
2. types in
 $\mathbf {K}$
are
$\mathbf {K}$
are
 $\omega $
-local.
$\omega $
-local.
Proof For (1), it suffices to prove that for any regular
![]() $\lambda \geq {\aleph _0}$
,
$\lambda \geq {\aleph _0}$
,
![]() $\lambda $
-local character implies continuity of
$\lambda $
-local character implies continuity of
![]() $\mu $
-nonsplitting over chains of cofinality
$\mu $
-nonsplitting over chains of cofinality
![]() $\geq \lambda $
. Let
$\geq \lambda $
. Let
![]() $\langle M_i:i\leq \lambda \rangle $
be u-increasing and continuous. Suppose
$\langle M_i:i\leq \lambda \rangle $
be u-increasing and continuous. Suppose
![]() $p\in \operatorname {gS}(M_\lambda )$
satisfies
$p\in \operatorname {gS}(M_\lambda )$
satisfies
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
for all
$M_0$
for all
![]() $i<\lambda $
. By
$i<\lambda $
. By
![]() $\lambda $
-local character, p does not
$\lambda $
-local character, p does not
![]() $\mu $
-split over some
$\mu $
-split over some
![]() $M_i$
. If
$M_i$
. If
![]() $i=0$
we are done. Otherwise, we have
$i=0$
we are done. Otherwise, we have
![]() $M_0<_uM_i<_uM_{i+1}<_uM_\lambda $
. By assumption,
$M_0<_uM_i<_uM_{i+1}<_uM_\lambda $
. By assumption,
![]() $p\restriction M_{i+1}$
does not
$p\restriction M_{i+1}$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. By weak transitivity (Proposition 3.12), p does not
$M_0$
. By weak transitivity (Proposition 3.12), p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
as desired.
$M_0$
as desired.
For (2), let
![]() $\langle M_i:i\leq \lambda \rangle $
and p as above. By assumption
$\langle M_i:i\leq \lambda \rangle $
and p as above. By assumption
![]() $p\restriction M_1$
does not
$p\restriction M_1$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
and
$M_0$
and
![]() $M_1>_uM_0$
. By extension (Proposition 3.12), there is
$M_1>_uM_0$
. By extension (Proposition 3.12), there is
![]() $q\supseteq p\restriction M_1$
in
$q\supseteq p\restriction M_1$
in
![]() $\operatorname {gS}(M_\lambda )$
such that q does not
$\operatorname {gS}(M_\lambda )$
such that q does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. By monotonicity, for
$M_0$
. By monotonicity, for
![]() $2\leq i<\lambda $
,
$2\leq i<\lambda $
,
![]() $q\restriction M_i$
does not
$q\restriction M_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. Now
$M_0$
. Now
![]() $(q\restriction M_i)\restriction M_1=p\restriction M_1=(p\restriction M_i)\restriction M_1$
, we can use weak uniqueness (Proposition 3.12) to inductively show that
$(q\restriction M_i)\restriction M_1=p\restriction M_1=(p\restriction M_i)\restriction M_1$
, we can use weak uniqueness (Proposition 3.12) to inductively show that
![]() $q\restriction M_i=p\restriction M_i$
for all
$q\restriction M_i=p\restriction M_i$
for all
![]() $i<\lambda $
. By
$i<\lambda $
. By
![]() $\omega $
-locality,
$\omega $
-locality,
![]() $p=q$
and the latter does not
$p=q$
and the latter does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
as desired.
$M_0$
as desired.
Once we have continuity of
![]() $\mu $
-nonsplitting in
$\mu $
-nonsplitting in
![]() $K_{\mu }$
, it automatically works for
$K_{\mu }$
, it automatically works for
![]() $K_{\geq \mu }$
.
$K_{\geq \mu }$
.
Proposition 3.17. Let
![]() $\delta $
be a limit ordinal,
$\delta $
be a limit ordinal,
![]() $\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$
be u-increasing and continuous,
$\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$
be u-increasing and continuous,
![]() $p\in \operatorname {gS}(M_\delta )$
. If for all
$p\in \operatorname {gS}(M_\delta )$
. If for all
![]() $i<\delta $
,
$i<\delta $
,
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
, then p also does not
$M_0$
, then p also does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
.
$M_0$
.
Proof The statement is vacuous when
![]() $M_0\in K_{>\mu }$
so we assume
$M_0\in K_{>\mu }$
so we assume
![]() $M_0\in K_{\mu }$
. By cofinality argument we may also assume
$M_0\in K_{\mu }$
. By cofinality argument we may also assume
![]() $\operatorname {cf}(\delta )\leq \mu $
. Suppose
$\operatorname {cf}(\delta )\leq \mu $
. Suppose
![]() $p \ \mu $
-splits over
$p \ \mu $
-splits over
![]() $M_0$
and pick witnesses
$M_0$
and pick witnesses
![]() $N^a$
and
$N^a$
and
![]() $N^b$
of size
$N^b$
of size
![]() $\mu $
. Using stability, define another u-increasing and continuous chain
$\mu $
. Using stability, define another u-increasing and continuous chain
![]() $\langle N_i:i\leq \delta \rangle \subseteq K_{\mu }$
such that:
$\langle N_i:i\leq \delta \rangle \subseteq K_{\mu }$
such that:
-
1. For
 $i\leq \delta $
,
$i\leq \delta $
,
 $N_i\leq M_i$
.
$N_i\leq M_i$
. -
2.
 $N_\delta $
contains
$N_\delta $
contains
 $N^a$
and
$N^a$
and
 $N^b$
.
$N^b$
. -
3.
 $N_0:= M_0$
.
$N_0:= M_0$
. -
4. For
 $i\leq \delta $
,
$i\leq \delta $
,
 $|N_i|\supseteq |M_i|\cap (|N^a|\cup |N^b|)$
.
$|N_i|\supseteq |M_i|\cap (|N^a|\cup |N^b|)$
.
By assumption each
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
, so by monotonicity
$M_0$
, so by monotonicity
![]() $p\restriction N_i$
does not
$p\restriction N_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_0=M_0$
. By continuity of
$N_0=M_0$
. By continuity of
![]() $\mu $
-nonsplitting,
$\mu $
-nonsplitting,
![]() $p\restriction N_\delta $
does not
$p\restriction N_\delta $
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_0$
, contradicting item (2) above.
$N_0$
, contradicting item (2) above.
4 Good frame over
 $(\geq \chi )$
-limit models except symmetry
$(\geq \chi )$
-limit models except symmetry
As seen in Proposition 3.12,
![]() $\mu $
-nonsplitting only satisfies weak transitivity but not transitivity, which is a key property of a good frame. We will adapt [Reference Vasey33, Definitions 3.8 and 4.2] to define nonforking from nonsplitting to solve this problem.
$\mu $
-nonsplitting only satisfies weak transitivity but not transitivity, which is a key property of a good frame. We will adapt [Reference Vasey33, Definitions 3.8 and 4.2] to define nonforking from nonsplitting to solve this problem.
Definition 4.1. Let
![]() $M\leq N$
in
$M\leq N$
in
![]() $K_{\geq \mu }$
and
$K_{\geq \mu }$
and
![]() $p\in \operatorname {gS}(N)$
.
$p\in \operatorname {gS}(N)$
.
-
1. p (explicitly) does not
 $\mu $
-fork over
$\mu $
-fork over
 $(M_0,M)$
if
$(M_0,M)$
if
 $M_0\in K_{\mu }$
,
$M_0\in K_{\mu }$
,
 $M_0<_uM$
and p does not
$M_0<_uM$
and p does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
.
$M_0$
. -
2. p does not
 $\mu $
-fork over M if there exists
$\mu $
-fork over M if there exists
 $M_0$
satisfying (1).
$M_0$
satisfying (1).
We call
![]() $M_0$
the witness to
$M_0$
the witness to
![]() $\mu $
-nonforking over M.
$\mu $
-nonforking over M.
The main difficulty of the above definition is that different
![]() $\mu $
-nonforkings over M may have different witnesses. For extension, the original approach in [Reference Vasey33] was to work in
$\mu $
-nonforkings over M may have different witnesses. For extension, the original approach in [Reference Vasey33] was to work in
![]() $\mu ^+$
-saturated models. Later [Reference VanDieren and Vasey31, Proposition 5.1] replaced it by superstability in an interval, which works for
$\mu ^+$
-saturated models. Later [Reference VanDieren and Vasey31, Proposition 5.1] replaced it by superstability in an interval, which works for
![]() $K_{\geq \mu }$
. We weaken the assumption to stability in an interval and continuity of
$K_{\geq \mu }$
. We weaken the assumption to stability in an interval and continuity of
![]() $\mu $
-nonsplitting, and use a direct limit argument similar to that of [Reference Boney4, Theorem 5.3].
$\mu $
-nonsplitting, and use a direct limit argument similar to that of [Reference Boney4, Theorem 5.3].
Proposition 4.2 (Extension).
Let
![]() $M\leq N\leq N'$
in
$M\leq N\leq N'$
in
![]() $K_{\geq \mu }$
. If
$K_{\geq \mu }$
. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\Vert N \Vert ,\Vert N' \Vert ]$
and
$[\Vert N \Vert ,\Vert N' \Vert ]$
and
![]() $p\in \operatorname {gS}(N)$
does not
$p\in \operatorname {gS}(N)$
does not
![]() $\mu $
-fork over M, then there is
$\mu $
-fork over M, then there is
![]() $q\supseteq p$
in
$q\supseteq p$
in
![]() $\operatorname {gS}(N')$
such that q does not
$\operatorname {gS}(N')$
such that q does not
![]() $\mu $
-fork over M.
$\mu $
-fork over M.
Proof Since p does not
![]() $\mu $
-fork over M, we can find witness
$\mu $
-fork over M, we can find witness
![]() $M_0\in K_{\mu }$
such that
$M_0\in K_{\mu }$
such that
![]() $M_0<_uM$
and p does not
$M_0<_uM$
and p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. If
$M_0$
. If
![]() $\Vert N \Vert =\Vert N' \Vert $
, we can use extension of nonsplitting (Proposition 3.12) to obtain (the unique)
$\Vert N \Vert =\Vert N' \Vert $
, we can use extension of nonsplitting (Proposition 3.12) to obtain (the unique)
![]() $q\in \operatorname {gS}(N')$
extending p which does not
$q\in \operatorname {gS}(N')$
extending p which does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. By definition q does not
$M_0$
. By definition q does not
![]() $\mu $
-fork over M.
$\mu $
-fork over M.
If
![]() $\Vert N \Vert {\kern-1.5pt}<{\kern-1.5pt}\Vert N' \Vert $
, first we assume
$\Vert N \Vert {\kern-1.5pt}<{\kern-1.5pt}\Vert N' \Vert $
, first we assume
![]() $N<_uN'$
and resolve
$N<_uN'$
and resolve
![]() $N'{\kern-1.5pt}={\kern-1.5pt}\bigcup \{N_i:i{\kern-1.5pt}\leq{\kern-1.5pt} \alpha +1\}$
u-increasing and continuous where
$N'{\kern-1.5pt}={\kern-1.5pt}\bigcup \{N_i:i{\kern-1.5pt}\leq{\kern-1.5pt} \alpha +1\}$
u-increasing and continuous where
![]() $N_0=N$
,
$N_0=N$
,
![]() $\Vert N_{\alpha } \Vert =\Vert N' \Vert $
,
$\Vert N_{\alpha } \Vert =\Vert N' \Vert $
,
![]() $N_{\alpha +1}=N'$
. The construction is possible by stability in
$N_{\alpha +1}=N'$
. The construction is possible by stability in
![]() $[\Vert N \Vert ,\Vert N' \Vert ]$
. We will define a coherent sequence
$[\Vert N \Vert ,\Vert N' \Vert ]$
. We will define a coherent sequence
![]() $\langle p_i:i\leq \alpha \rangle $
such that
$\langle p_i:i\leq \alpha \rangle $
such that
![]() $p_i$
is a nonsplitting extension of p in
$p_i$
is a nonsplitting extension of p in
![]() $\operatorname {gS}(N_i)$
. The first paragraph gives the successor step. For limit step
$\operatorname {gS}(N_i)$
. The first paragraph gives the successor step. For limit step
![]() $\delta \leq \alpha $
, we take the direct limit to obtain an extension
$\delta \leq \alpha $
, we take the direct limit to obtain an extension
![]() $p_\delta $
of
$p_\delta $
of
![]() $\langle p_i:i<\delta \rangle $
. Since all previous
$\langle p_i:i<\delta \rangle $
. Since all previous
![]() $p_i$
does not
$p_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
, by Proposition 3.17,
$M_0$
, by Proposition 3.17,
![]() $p_\delta $
also does not
$p_\delta $
also does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. After the construction has finished, we obtain
$M_0$
. After the construction has finished, we obtain
![]() $q:= p_{\alpha }$
a nonsplitting extension of p in
$q:= p_{\alpha }$
a nonsplitting extension of p in
![]() $\operatorname {gS}(N')$
. Since
$\operatorname {gS}(N')$
. Since
![]() $M_0<_uM\leq N'$
, we still have q does not
$M_0<_uM\leq N'$
, we still have q does not
![]() $\mu $
-fork over M.
$\mu $
-fork over M.
In the general case where
![]() $N\leq N'$
, extend
$N\leq N'$
, extend
![]() $N'<_u N"$
with
$N'<_u N"$
with
![]() $\Vert N" \Vert =\Vert N' \Vert $
. Then we can extend p to a nonforking
$\Vert N" \Vert =\Vert N' \Vert $
. Then we can extend p to a nonforking
![]() $q"\in \operatorname {gS}(N")$
and use monotonicity to obtain the desired q.
$q"\in \operatorname {gS}(N")$
and use monotonicity to obtain the desired q.
Corollary 4.3. Let
![]() $M_0<_u M\leq N'$
with
$M_0<_u M\leq N'$
with
![]() $M_0\in K_{\mu }$
. If
$M_0\in K_{\mu }$
. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\Vert M \Vert ,\Vert N' \Vert ]$
and
$[\Vert M \Vert ,\Vert N' \Vert ]$
and
![]() $p\in \operatorname {gS}(M)$
does not
$p\in \operatorname {gS}(M)$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
, then there is
$M_0$
, then there is
![]() $q\supseteq p$
in
$q\supseteq p$
in
![]() $\operatorname {gS}(N')$
such that q does not
$\operatorname {gS}(N')$
such that q does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
.
$M_0$
.
Proof Run through the exact same proof as in Proposition 4.2, where
![]() $M=N$
and
$M=N$
and
![]() $M_0$
is given in the hypothesis.
$M_0$
is given in the hypothesis.
For continuity, the original approach in [Reference Vasey33, Lemma 4.12] was to deduce it from superstability (which we do not assume) and transitivity. Transitivity there was obtained from extension and uniqueness, and uniqueness was proved in [Reference Vasey33, Lemma 5.3] for
![]() $\mu ^+$
-saturated models only (or assuming superstability in [Reference Vasey35, Lemma 2.12]). Our new argument uses weak transitivity and continuity of
$\mu ^+$
-saturated models only (or assuming superstability in [Reference Vasey35, Lemma 2.12]). Our new argument uses weak transitivity and continuity of
![]() $\mu $
-nonsplitting to show that continuity of
$\mu $
-nonsplitting to show that continuity of
![]() $\mu $
-nonforking holds for a universally increasing chain in
$\mu $
-nonforking holds for a universally increasing chain in
![]() $K_{\mu }$
. The case in
$K_{\mu }$
. The case in
![]() $K_{\geq \mu }$
will be proved after we have developed transitivity and local character of nonforking.
$K_{\geq \mu }$
will be proved after we have developed transitivity and local character of nonforking.
Proposition 4.4 (Continuity 1).
Let
![]() $\delta <\mu ^+$
be a limit ordinal and
$\delta <\mu ^+$
be a limit ordinal and
![]() $\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$
be u-increasing and continuous. Let
$\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$
be u-increasing and continuous. Let
![]() $p\in \operatorname {gS}(M_\delta )$
satisfy
$p\in \operatorname {gS}(M_\delta )$
satisfy
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
for all
$M_0$
for all
![]() $1\leq i<\delta $
. Then p also does not
$1\leq i<\delta $
. Then p also does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
.
$M_0$
.
Proof For
![]() $1\leq i<\delta $
, since
$1\leq i<\delta $
, since
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
, we can find
$M_0$
, we can find
![]() $M^i<_uM_0$
of size
$M^i<_uM_0$
of size
![]() $\mu $
such that
$\mu $
such that
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M^i$
. By monotonicity of nonsplitting,
$M^i$
. By monotonicity of nonsplitting,
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. By continuity of
$M_0$
. By continuity of
![]() $\mu $
-nonsplitting, p does not
$\mu $
-nonsplitting, p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. Since
$M_0$
. Since
![]() $M^1<_u M_0<_u M_1<_u M_\delta $
, by weak transitivity (Proposition 3.12) p does not
$M^1<_u M_0<_u M_1<_u M_\delta $
, by weak transitivity (Proposition 3.12) p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M^1$
. (By a similar argument, it does not
$M^1$
. (By a similar argument, it does not
![]() $\mu $
-split over other
$\mu $
-split over other
![]() $M^i$
.) By definition p does not
$M^i$
.) By definition p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
.
$M_0$
.
We now show uniqueness of nonforking in
![]() $K_{\mu }$
, by generalizing the argument in [Reference Vasey35]. Instead of superstability, we stick to our Assumption 2.1. Fact 2.9 in that paper will be replaced by our Proposition 4.2. The requirement that
$K_{\mu }$
, by generalizing the argument in [Reference Vasey35]. Instead of superstability, we stick to our Assumption 2.1. Fact 2.9 in that paper will be replaced by our Proposition 4.2. The requirement that
![]() $M_0,M_1$
be limit models is removed.
$M_0,M_1$
be limit models is removed.
Proposition 4.5 (Uniqueness 1).
Let
![]() $M_0\leq M_1$
in
$M_0\leq M_1$
in
![]() $K_{\mu }$
and
$K_{\mu }$
and
![]() $p_0\neq p_1\in \operatorname {gS}(M_1)$
both do not
$p_0\neq p_1\in \operatorname {gS}(M_1)$
both do not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
. If in addition
$M_0$
. If in addition
![]() $p_{\langle \rangle }:= p_0\restriction M_0=p_1\restriction M_0$
, then
$p_{\langle \rangle }:= p_0\restriction M_0=p_1\restriction M_0$
, then
![]() $p_0=p_1$
.
$p_0=p_1$
.
Proof Suppose the proposition is false. Let
![]() $N_0<_u M_0$
and
$N_0<_u M_0$
and
![]() $N_1<_uM_0$
such that
$N_1<_uM_0$
such that
![]() $p_0$
does not
$p_0$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_0$
while
$N_0$
while
![]() $p_1$
does not
$p_1$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_1$
(necessarily
$N_1$
(necessarily
![]() $N_0\neq N_1$
by weak uniqueness of nonsplitting). We will build a u-increasing and continuous
$N_0\neq N_1$
by weak uniqueness of nonsplitting). We will build a u-increasing and continuous
![]() $\langle M_i:i\leq \mu \rangle \subseteq K_{\mu }$
and a coherent
$\langle M_i:i\leq \mu \rangle \subseteq K_{\mu }$
and a coherent
![]() $\langle p_\eta \in \operatorname {gS}(M_{l(\eta )}):\eta \in 2^{\leq \mu }\rangle $
such that for all
$\langle p_\eta \in \operatorname {gS}(M_{l(\eta )}):\eta \in 2^{\leq \mu }\rangle $
such that for all
![]() $\nu \in 2^{<\mu }$
,
$\nu \in 2^{<\mu }$
,
![]() $p_{\nu ^\frown 0}$
and
$p_{\nu ^\frown 0}$
and
![]() $p_{\nu ^\frown 1}$
are distinct nonforking extensions of
$p_{\nu ^\frown 1}$
are distinct nonforking extensions of
![]() $p_{\nu }$
. If done
$p_{\nu }$
. If done
![]() $\{p_\eta :\eta \in 2^\mu \}$
will contradict stability in
$\{p_\eta :\eta \in 2^\mu \}$
will contradict stability in
![]() $\mu $
.
$\mu $
.
The base case is given by the assumption. For successor case, suppose
![]() $M_i$
and
$M_i$
and
![]() $\{p_\eta :\eta \in 2^i\}$
have been constructed for some
$\{p_\eta :\eta \in 2^i\}$
have been constructed for some
![]() $1\leq i<\mu $
. Define
$1\leq i<\mu $
. Define
![]() $M_{i+1}'$
to be a
$M_{i+1}'$
to be a
![]() $(\mu ,\omega )$
-limit over
$(\mu ,\omega )$
-limit over
![]() $M_i$
. Fix
$M_i$
. Fix
![]() $\eta \in 2^i$
, we will define
$\eta \in 2^i$
, we will define
![]() $p_{\eta ^\frown 0},p_{\eta ^\frown 1}\in \operatorname {gS}(M_{i+1}')$
nonforking extensions of
$p_{\eta ^\frown 0},p_{\eta ^\frown 1}\in \operatorname {gS}(M_{i+1}')$
nonforking extensions of
![]() $p_\eta $
(nonsplitting will be witnessed by different models; otherwise weak uniqueness of nonsplitting applies). Since
$p_\eta $
(nonsplitting will be witnessed by different models; otherwise weak uniqueness of nonsplitting applies). Since
![]() $p_\eta $
does not
$p_\eta $
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
, we can find
$M_0$
, we can find
![]() $N_{\eta }<_uM_0$
such that
$N_{\eta }<_uM_0$
such that
![]() $p_\eta $
does not
$p_\eta $
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_\eta $
. Pick
$N_\eta $
. Pick
![]() $p_\eta ^+\in \operatorname {gS}(M_{i+1}')$
a nonsplitting extension of
$p_\eta ^+\in \operatorname {gS}(M_{i+1}')$
a nonsplitting extension of
![]() $p_\eta $
. On the other hand, obtain
$p_\eta $
. On the other hand, obtain
![]() $N_\eta '<_uN^*<_uM_0$
such that
$N_\eta '<_uN^*<_uM_0$
such that
![]() $N^*$
is a
$N^*$
is a
![]() $(\mu ,\omega )$
-limit over
$(\mu ,\omega )$
-limit over
![]() $N_\eta '$
and
$N_\eta '$
and
![]() $N_\eta '>_uN_\eta $
. By uniqueness of limit models over
$N_\eta '>_uN_\eta $
. By uniqueness of limit models over
![]() $N_\eta $
of the same length, there is
$N_\eta $
of the same length, there is
![]() $f:M_{i+1}'\cong _{N_\eta '}N^*$
.
$f:M_{i+1}'\cong _{N_\eta '}N^*$
.

By invariance of nonsplitting,
![]() $f(p_\eta ^+)$
does not
$f(p_\eta ^+)$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_\eta $
. By monotonicity of nonsplitting,
$N_\eta $
. By monotonicity of nonsplitting,
![]() $p_\eta $
, and hence
$p_\eta $
, and hence
![]() $p_\eta \restriction N^*$
does not
$p_\eta \restriction N^*$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_\eta $
.
$N_\eta $
.
![]() $f(p_\eta ^+)\restriction N_\eta '=p_\eta ^+\restriction N_\eta '=(p_\eta \restriction N^*)\restriction N_\eta '$
. By weak uniqueness of
$f(p_\eta ^+)\restriction N_\eta '=p_\eta ^+\restriction N_\eta '=(p_\eta \restriction N^*)\restriction N_\eta '$
. By weak uniqueness of
![]() $\mu $
-nonsplitting,
$\mu $
-nonsplitting,
![]() $f(p_\eta ^+)=p_\eta \restriction N^*$
. Since
$f(p_\eta ^+)=p_\eta \restriction N^*$
. Since
![]() $p_\eta \restriction N^*$
has two nonforking extensions
$p_\eta \restriction N^*$
has two nonforking extensions
![]() $p_0\neq p_1\in \operatorname {gS}(M_1)$
where
$p_0\neq p_1\in \operatorname {gS}(M_1)$
where
![]() $M_1>_uN^*$
, we can obtain their isomorphic copies
$M_1>_uN^*$
, we can obtain their isomorphic copies
![]() $p_{\eta ^\frown 0}\neq p_{\eta ^\frown 1}\in \operatorname {gS}(M_{i+1})$
for some
$p_{\eta ^\frown 0}\neq p_{\eta ^\frown 1}\in \operatorname {gS}(M_{i+1})$
for some
![]() $M_{i+1}>_uM_{i+1}'$
. They still do not
$M_{i+1}>_uM_{i+1}'$
. They still do not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
because
$M_0$
because
![]() $M_0$
is fixed (actually
$M_0$
is fixed (actually
![]() $p_{\eta ^\frown i}$
does not
$p_{\eta ^\frown i}$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_i<_uM_0$
). Ensure coherence at the end.
$N_i<_uM_0$
). Ensure coherence at the end.
For limit case, let
![]() $\eta \in 2^\delta $
for some limit ordinal
$\eta \in 2^\delta $
for some limit ordinal
![]() $\delta \leq \mu $
. Define
$\delta \leq \mu $
. Define
![]() $p_\eta \in \operatorname {gS}(M_\delta )$
to be the direct limit of
$p_\eta \in \operatorname {gS}(M_\delta )$
to be the direct limit of
![]() $\langle p_{\eta \restriction i}:i<\delta \rangle $
. By Proposition 4.4,
$\langle p_{\eta \restriction i}:i<\delta \rangle $
. By Proposition 4.4,
![]() $p_\eta $
does not
$p_\eta $
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
.
$M_0$
.
Corollary 4.6 (Uniqueness 2).
Let
![]() $M\leq N$
in
$M\leq N$
in
![]() $K_{\geq \mu }$
and
$K_{\geq \mu }$
and
![]() $p,q\in \operatorname {gS}(N)$
both do not
$p,q\in \operatorname {gS}(N)$
both do not
![]() $\mu $
-fork over M. If in addition
$\mu $
-fork over M. If in addition
![]() $p\restriction M=q\restriction M$
, then
$p\restriction M=q\restriction M$
, then
![]() $p=q$
.
$p=q$
.
Proof Proposition 4.5 takes care of the case
![]() $M,N\in K_{\mu }$
. Suppose the corollary is false, then
$M,N\in K_{\mu }$
. Suppose the corollary is false, then
![]() $p\neq q$
and there exist
$p\neq q$
and there exist
![]() $N^p,N^q<_uM$
such that p does not
$N^p,N^q<_uM$
such that p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $N^p$
and q does not
$N^p$
and q does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $N^q$
. We have two cases:
$N^q$
. We have two cases:
-
1. Suppose
 $M\in K_{\mu }$
but
$M\in K_{\mu }$
but
 $N\in K_{>\mu }$
. By tameness obtain
$N\in K_{>\mu }$
. By tameness obtain
 $N'\in K_{\mu }$
such that
$N'\in K_{\mu }$
such that
 $M\leq N'\leq N$
and
$M\leq N'\leq N$
and
 $p\restriction N'\neq q\restriction N'$
. Together with
$p\restriction N'\neq q\restriction N'$
. Together with
 $p\restriction M=q\restriction M$
, it contradicts Proposition 4.5.
$p\restriction M=q\restriction M$
, it contradicts Proposition 4.5. -
2. Suppose
 $M\in K_{>\mu }$
. Obtain
$M\in K_{>\mu }$
. Obtain
 $M^p,M^q\leq M$
of size
$M^p,M^q\leq M$
of size
 $\mu $
that are universal over
$\mu $
that are universal over
 $N^p$
and
$N^p$
and
 $N^q$
, respectively. By Löwenheim–Skolem axiom, pick
$N^q$
, respectively. By Löwenheim–Skolem axiom, pick
 $M'\leq M$
of size
$M'\leq M$
of size
 $\mu $
containing
$\mu $
containing
 $M^p$
and
$M^p$
and
 $M^q$
. Thus
$M^q$
. Thus
 $M'$
is universal over both
$M'$
is universal over both
 $N^p$
and
$N^p$
and
 $N^q$
, and
$N^q$
, and
 $p\restriction M'=q\restriction M'$
. Since
$p\restriction M'=q\restriction M'$
. Since
 $p\neq q$
, tameness gives some
$p\neq q$
, tameness gives some
 $N'\in K_{\mu }$
,
$N'\in K_{\mu }$
,
 $M'\leq N'\leq N$
such that
$M'\leq N'\leq N$
such that
 $p\restriction N'\neq q\restriction N'$
, which contradicts Proposition 4.5.
$p\restriction N'\neq q\restriction N'$
, which contradicts Proposition 4.5.
Remark 4.7. The strategy of case (2) cannot be applied to Proposition 4.5 because
![]() $M'$
might coincide with M and we do not have enough room to invoke weak uniqueness of nonsplitting. This calls for a specific proof in Proposition 4.5. Similarly, we cannot simply invoke weak uniqueness of nonsplitting to prove case (2) because we do not know if M is also universal over
$M'$
might coincide with M and we do not have enough room to invoke weak uniqueness of nonsplitting. This calls for a specific proof in Proposition 4.5. Similarly, we cannot simply invoke weak uniqueness of nonsplitting to prove case (2) because we do not know if M is also universal over
![]() $M'$
.
$M'$
.
Corollary 4.8 (Transitivity).
Let
![]() $M_0\leq M_1\leq M_2$
be in
$M_0\leq M_1\leq M_2$
be in
![]() $K_{\geq \mu }$
,
$K_{\geq \mu }$
,
![]() $p\in \operatorname {gS}(M_2)$
. If
$p\in \operatorname {gS}(M_2)$
. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\Vert M_1 \Vert ,\Vert M_2 \Vert ]$
, p does not
$[\Vert M_1 \Vert ,\Vert M_2 \Vert ]$
, p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_1$
and
$M_1$
and
![]() $p\restriction M_1$
does not
$p\restriction M_1$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
, then p does not
$M_0$
, then p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
.
$M_0$
.
Proof By Proposition 4.2, obtain
![]() $q\supseteq p\restriction M_1$
a nonforking extension in
$q\supseteq p\restriction M_1$
a nonforking extension in
![]() $\operatorname {gS}(M_2)$
. Both q and p do not fork over
$\operatorname {gS}(M_2)$
. Both q and p do not fork over
![]() $M_1$
and
$M_1$
and
![]() $q\restriction M_1=p\restriction M_1$
. By Corollary 4.6,
$q\restriction M_1=p\restriction M_1$
. By Corollary 4.6,
![]() $p=q$
, but q does not
$p=q$
, but q does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
.
$M_0$
.
For local character, we imitate [Reference Vasey33, Lemma 4.11] which handled the case of
![]() $\mu ^+$
-saturated models ordered by
$\mu ^+$
-saturated models ordered by
![]() $\leq _{\mathbf {K}}$
instead of
$\leq _{\mathbf {K}}$
instead of
![]() $<_u$
. That proof originates from [Reference Shelah24, II Claim 2.11(5)].
$<_u$
. That proof originates from [Reference Shelah24, II Claim 2.11(5)].
Proposition 4.9 (Local character).
Let
![]() $\delta \geq \chi $
be regular,
$\delta \geq \chi $
be regular,
![]() $\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$
u-increasing and continuous,
$\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$
u-increasing and continuous,
![]() $p\in \operatorname {gS}(M_\delta )$
. There is
$p\in \operatorname {gS}(M_\delta )$
. There is
![]() $i<\delta $
such that p does not
$i<\delta $
such that p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_i$
.
$M_i$
.
Proof If
![]() $\delta \geq \mu ^+$
, then by existence of nonsplitting (Proposition 3.12) and monotonicity, there is
$\delta \geq \mu ^+$
, then by existence of nonsplitting (Proposition 3.12) and monotonicity, there is
![]() $j<\delta $
such that p does not
$j<\delta $
such that p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_j$
. As
$M_j$
. As
![]() $M_{j+1}$
is universal over
$M_{j+1}$
is universal over
![]() $M_j$
, p does not
$M_j$
, p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_{j+1}$
.
$M_{j+1}$
.
If
![]() $\chi \leq \delta \leq \mu $
and suppose the conclusion fails, then we can build:
$\chi \leq \delta \leq \mu $
and suppose the conclusion fails, then we can build:
-
1.
 $\langle N_i:i\leq \delta \rangle \subseteq K_{\mu }$
u-increasing and continuous.
$\langle N_i:i\leq \delta \rangle \subseteq K_{\mu }$
u-increasing and continuous. -
2.
 $\langle N_i':i\leq \delta \rangle \subseteq K_{\mu }$
increasing and continuous.
$\langle N_i':i\leq \delta \rangle \subseteq K_{\mu }$
increasing and continuous. -
3.
 $N_0=N_0'\leq M_0$
be any model in
$N_0=N_0'\leq M_0$
be any model in
 $K_{\mu }$
.
$K_{\mu }$
. -
4. For all
 $i<\delta $
,
$i<\delta $
,
 $N_i\leq M_i$
and
$N_i\leq M_i$
and
 $N_i\leq N_i'\leq M_\delta $
.
$N_i\leq N_i'\leq M_\delta $
. -
5. For all
 $i<\delta $
,
$i<\delta $
,
 $\bigcup _{j\leq i}(|N_j'|\cap |M_{i+1}|)\subseteq |N_{i+1}|.$
$\bigcup _{j\leq i}(|N_j'|\cap |M_{i+1}|)\subseteq |N_{i+1}|.$
-
6. For all
 $j<\delta $
,
$j<\delta $
,
 $p\restriction N_{j+1}' \ \mu $
-splits over
$p\restriction N_{j+1}' \ \mu $
-splits over
 $N_j$
.
$N_j$
.
We specify the successor step of
![]() $N_i'$
: suppose
$N_i'$
: suppose
![]() $N_i$
has been constructed. Since
$N_i$
has been constructed. Since
![]() $p \mu $
-forks over
$p \mu $
-forks over
![]() $M_i$
, hence over
$M_i$
, hence over
![]() $N_i$
. Thus
$N_i$
. Thus
![]() $(N_{i-1},N_i)$
cannot witness nonforking, so there is
$(N_{i-1},N_i)$
cannot witness nonforking, so there is
![]() $N_i'\in K_{\mu }$
with
$N_i'\in K_{\mu }$
with
![]() $N_i\leq N_i'\leq M_\delta $
such that
$N_i\leq N_i'\leq M_\delta $
such that
![]() $p\restriction N_i' \ \mu $
-splits over
$p\restriction N_i' \ \mu $
-splits over
![]() $N_{i-1}$
. After the construction, by monotonicity
$N_{i-1}$
. After the construction, by monotonicity
![]() $p\restriction N_\delta \supseteq p\restriction N_i' \ \mu $
-splits over
$p\restriction N_\delta \supseteq p\restriction N_i' \ \mu $
-splits over
![]() $N_{i-1}$
for each successor i, contradicting
$N_{i-1}$
for each successor i, contradicting
![]() $\chi $
-local character of
$\chi $
-local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
In Section 6, we will need the original form of [Reference Vasey33, Lemma 4.11], whose proof is similar to Proposition 4.9. We write the statement here for comparison.
Fact 4.10. Let
![]() $\delta \geq \chi $
be regular,
$\delta \geq \chi $
be regular,
![]() $\langle M_i:i\leq \delta \rangle $
be an increasing and continuous chain of
$\langle M_i:i\leq \delta \rangle $
be an increasing and continuous chain of
![]() $\mu ^+$
-saturated models,
$\mu ^+$
-saturated models,
![]() $p\in \operatorname {gS}(M_\delta )$
. There is
$p\in \operatorname {gS}(M_\delta )$
. There is
![]() $i<\delta $
such that p does not
$i<\delta $
such that p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_i$
.
$M_i$
.
We now show the promised continuity of nonforking. In [Reference Vasey33, Lemma 4.12], the chain must be of length
![]() $\geq \chi $
. We do not have the restriction here because we have continuity of nonsplitting in Assumption 2.1.
$\geq \chi $
. We do not have the restriction here because we have continuity of nonsplitting in Assumption 2.1.
Proposition 4.11 (Continuity 2).
Let
![]() $\delta <\mu ^+$
be regular,
$\delta <\mu ^+$
be regular,
![]() $\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$
u-increasing and continuous, and
$\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$
u-increasing and continuous, and
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\Vert M_1 \Vert ,\Vert M_\delta \Vert )$
. Let
$[\Vert M_1 \Vert ,\Vert M_\delta \Vert )$
. Let
![]() $p\in \operatorname {gS}(M_\delta )$
satisfy
$p\in \operatorname {gS}(M_\delta )$
satisfy
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
for all
$M_0$
for all
![]() $1\leq i<\delta $
. Then p also does not
$1\leq i<\delta $
. Then p also does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
.
$M_0$
.
Proof If
![]() $\delta \geq \chi $
, by Proposition 4.9 there is
$\delta \geq \chi $
, by Proposition 4.9 there is
![]() $i<\delta $
such that p does not
$i<\delta $
such that p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_i$
. By Corollary 4.8, p does not
$M_i$
. By Corollary 4.8, p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
.
$M_0$
.
If
![]() $\delta <\chi \leq \mu $
, we have two cases: (1)
$\delta <\chi \leq \mu $
, we have two cases: (1)
![]() $M_0\in K_{\mu }$
: then for
$M_0\in K_{\mu }$
: then for
![]() $1\leq i<\delta $
,
$1\leq i<\delta $
,
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
. By Proposition 3.17, p does not
$M_0$
. By Proposition 3.17, p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_0$
, so p does not
$M_0$
, so p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_1$
. By Corollary 4.8, p does not
$M_1$
. By Corollary 4.8, p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
. (2)
$M_0$
. (2)
![]() $M_0\in K_{>\mu }$
: for
$M_0\in K_{>\mu }$
: for
![]() $1\leq i<\delta $
, let
$1\leq i<\delta $
, let
![]() $N_i<_u M_0$
witness
$N_i<_u M_0$
witness
![]() $p\restriction M_i$
does not
$p\restriction M_i$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
. By Löwenheim–Skolem axiom, there is
$M_0$
. By Löwenheim–Skolem axiom, there is
![]() $N\in K_{\mu }$
(here we need
$N\in K_{\mu }$
(here we need
![]() $\delta \leq \mu $
) such that
$\delta \leq \mu $
) such that
![]() $N_i<_uN\leq M_0$
for all i. Apply case (1) with N replacing
$N_i<_uN\leq M_0$
for all i. Apply case (1) with N replacing
![]() $M_0$
.
$M_0$
.
Existence is more tricky because nonforking requires the base to be universal over the witness of nonsplitting. The second part of the proof is based on [Reference Vasey33, Lemma 4.9].
Proposition 4.12 (Existence).
Let M be a
![]() $(\geq \mu ,\geq \chi )$
-limit model,
$(\geq \mu ,\geq \chi )$
-limit model,
![]() $p\in \operatorname {gS}(M)$
. Then p does not
$p\in \operatorname {gS}(M)$
. Then p does not
![]() $\mu $
-fork over M. Alternatively M can be a
$\mu $
-fork over M. Alternatively M can be a
![]() $\mu ^+$
-saturated model.
$\mu ^+$
-saturated model.
Proof The first part is immediate from Proposition 4.9. For the second part, apply existence of nonsplitting Proposition 3.12 to obtain
![]() $N\in K_{\mu }$
,
$N\in K_{\mu }$
,
![]() $N\leq M$
such that p does not
$N\leq M$
such that p does not
![]() $\mu $
-split over N. By model-homogeneity, M is universal over N, hence p does not
$\mu $
-split over N. By model-homogeneity, M is universal over N, hence p does not
![]() $\mu $
-fork over M.
$\mu $
-fork over M.
Corollary 4.13. There exists a good
![]() $\mu $
-frame over the
$\mu $
-frame over the
![]() $\mu $
-skeleton of
$\mu $
-skeleton of
![]() $(\mu ,\geq \chi )$
-limit models ordered by
$(\mu ,\geq \chi )$
-limit models ordered by
![]() $\leq _u$
, except for symmetry and local character
$\leq _u$
, except for symmetry and local character
![]() $\chi $
in place of
$\chi $
in place of
![]() ${\aleph _0}$
.
${\aleph _0}$
.
Proof Define nonforking as in Definition 4.1(2). Invariance and monotonicity are immediate. Existence is by Proposition 4.12,
![]() $\chi $
-local character is by Proposition 4.9, extension is by Proposition 4.2, uniqueness is by Proposition 4.5, and continuity is by Proposition 4.4.
$\chi $
-local character is by Proposition 4.9, extension is by Proposition 4.2, uniqueness is by Proposition 4.5, and continuity is by Proposition 4.4.
Remark 4.14.
-
1. We do not expect
 $\aleph _0$
-local character because there are strictly stable AECs. For the same reason we restrict models to be
$\aleph _0$
-local character because there are strictly stable AECs. For the same reason we restrict models to be
 $(\mu ,\geq \chi )$
-limit to guarantee existence property.
$(\mu ,\geq \chi )$
-limit to guarantee existence property. -
2. Let
 $\lambda \geq \mu $
. Our frame extends to
$\lambda \geq \mu $
. Our frame extends to
 $([\mu ,\lambda ],\geq \chi )$
-limit models if we assume stability in
$([\mu ,\lambda ],\geq \chi )$
-limit models if we assume stability in
 $[\mu ,\lambda ]$
. However [Reference Vasey33] has already developed
$[\mu ,\lambda ]$
. However [Reference Vasey33] has already developed
 $\mu $
-nonforking for
$\mu $
-nonforking for
 $\mu ^+$
-saturated models ordered by
$\mu ^+$
-saturated models ordered by
 $\leq $
, and we will see in Corollary 6.2(2) that under extra stability assumptions,
$\leq $
, and we will see in Corollary 6.2(2) that under extra stability assumptions,
 $(>\mu ,\geq \chi )$
-limit models are automatically
$(>\mu ,\geq \chi )$
-limit models are automatically
 $\mu ^+$
-saturated, so the interesting part is
$\mu ^+$
-saturated, so the interesting part is
 $K_{\mu }$
here.
$K_{\mu }$
here. -
3. We will see in Corollary 5.13(2) that symmetry also holds if we have enough stability.
Since we have built an approximation of a good frame in Corollary 4.13, one might ask if it is canonical. We first observe the following fact (Assumption 2.1 is not needed):
Fact 4.15 [Reference Vasey37, Theorem 14.1].
Let
![]() $\lambda \geq \operatorname {LS}(\mathbf {K})$
. Suppose
$\lambda \geq \operatorname {LS}(\mathbf {K})$
. Suppose
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\lambda $
-superstable and there is an independence relation over the limit models (ordered by
$\lambda $
-superstable and there is an independence relation over the limit models (ordered by
![]() $\leq $
) in
$\leq $
) in
![]() $K_\lambda $
, satisfying invariance, monotonicity, universal local character, uniqueness, and extension. Let
$K_\lambda $
, satisfying invariance, monotonicity, universal local character, uniqueness, and extension. Let
![]() $M\leq N$
be limit models in
$M\leq N$
be limit models in
![]() $K_\lambda $
and
$K_\lambda $
and
![]() $p\in \operatorname {gS}(N)$
. Then p is independent over M iff p does not
$p\in \operatorname {gS}(N)$
. Then p is independent over M iff p does not
![]() $\lambda $
-fork over M.
$\lambda $
-fork over M.
Its proof has the advantage that it does not require the independence relation to be for longer types as in [Reference Boney, Grossberg, Kolesnikov and Vasey7, Corollary 5.19]. However, it still uses the following lemma from [Reference Boney, Grossberg, Kolesnikov and Vasey7, Lemma 4.2]:
Lemma 4.16. Suppose there is an independence relation over models in
![]() $K_{\mu }$
ordered by
$K_{\mu }$
ordered by
![]() $\leq $
. If it satisfies invariance, monotonicity, and uniqueness, then the relation is extended by
$\leq $
. If it satisfies invariance, monotonicity, and uniqueness, then the relation is extended by
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
Proof Suppose
![]() $M\leq N$
in
$M\leq N$
in
![]() $K_{\mu }$
,
$K_{\mu }$
,
![]() $p\in \operatorname {gS}(N)$
is independent over M. For any
$p\in \operatorname {gS}(N)$
is independent over M. For any
![]() $N_1,N_2\in K_{\mu }$
with
$N_1,N_2\in K_{\mu }$
with
![]() $M\leq N_1,N_2\leq N$
, and any
$M\leq N_1,N_2\leq N$
, and any
![]() $f:N_1\cong _MN_2$
. We need to show that
$f:N_1\cong _MN_2$
. We need to show that
![]() $f(p)\restriction N_2=p\restriction N_2$
. By monotonicity,
$f(p)\restriction N_2=p\restriction N_2$
. By monotonicity,
![]() $p\restriction N_1$
and
$p\restriction N_1$
and
![]() $p\restriction N_2$
do not depend on M. By invariance,
$p\restriction N_2$
do not depend on M. By invariance,
![]() $f(p)\restriction N_2$
is independent over M. By uniqueness and the fact that f fixes M, we have
$f(p)\restriction N_2$
is independent over M. By uniqueness and the fact that f fixes M, we have
![]() $f(p)\restriction N_2=p\restriction N_2$
.
$f(p)\restriction N_2=p\restriction N_2$
.
In the above proof, it utilizes the assumption that the independence relation is for models ordered by
![]() $\leq $
, so it makes sense to talk about
$\leq $
, so it makes sense to talk about
![]() $p\restriction N_i$
is independent over M for
$p\restriction N_i$
is independent over M for
![]() $i=1,2$
. To generalize Fact 4.15 to our frame in Corollary 4.13, one way is to assume the independence relation to be for models ordered by
$i=1,2$
. To generalize Fact 4.15 to our frame in Corollary 4.13, one way is to assume the independence relation to be for models ordered by
![]() $\leq $
, and with universal local character
$\leq $
, and with universal local character
![]() $\chi $
. But since we defined our frame to be for models ordered by
$\chi $
. But since we defined our frame to be for models ordered by
![]() $\leq _u$
, we want to keep the weaker assumption that the arbitrary independence relation is also for models ordered by
$\leq _u$
, we want to keep the weaker assumption that the arbitrary independence relation is also for models ordered by
![]() $\leq _u$
. Thus we cannot directly invoke Lemma 4.16, where the
$\leq _u$
. Thus we cannot directly invoke Lemma 4.16, where the
![]() $N_i$
’s are not necessarily universal over M. To circumvent this, we adapt the lemma by allowing more room:
$N_i$
’s are not necessarily universal over M. To circumvent this, we adapt the lemma by allowing more room:
Lemma 4.17. Let
![]() $M<_uN<_uN'$
all in
$M<_uN<_uN'$
all in
![]() $K_{\mu }$
,
$K_{\mu }$
,
![]() $p\in \operatorname {gS}(N')$
. If
$p\in \operatorname {gS}(N')$
. If
![]() $p\restriction N \ \mu $
-splits over M, then p also
$p\restriction N \ \mu $
-splits over M, then p also
![]() $\mu $
-splits over M with witnesses universal over M. Namely, there are
$\mu $
-splits over M with witnesses universal over M. Namely, there are
![]() $N_1',N_2'\leq N'$
such that
$N_1',N_2'\leq N'$
such that
![]() $N_1'>_uM$
,
$N_1'>_uM$
,
![]() $N_2'>_uM$
and there is
$N_2'>_uM$
and there is
![]() $f':N_1'\cong _MN_2'$
with
$f':N_1'\cong _MN_2'$
with
![]() $f(p)\restriction N_2'\neq p\restriction N_2'$
.
$f(p)\restriction N_2'\neq p\restriction N_2'$
.
Proof By assumption, there are
![]() $N_1,N_2\in K_{\mu }$
such that
$N_1,N_2\in K_{\mu }$
such that
![]() $M\leq N_1,N_2\leq N$
and there is
$M\leq N_1,N_2\leq N$
and there is
![]() $f:N_1\cong _MN_2$
such that
$f:N_1\cong _MN_2$
such that
![]() $f(p\restriction N)\restriction N_2\neq p\restriction N_2$
. Extend f to an isomorphism
$f(p\restriction N)\restriction N_2\neq p\restriction N_2$
. Extend f to an isomorphism
![]() $\tilde {f}$
of codomain N, and let
$\tilde {f}$
of codomain N, and let
![]() $N^*\geq N_1$
be the domain of
$N^*\geq N_1$
be the domain of
![]() $\tilde {f}$
. Since
$\tilde {f}$
. Since
![]() $N>_uM$
, by invariance
$N>_uM$
, by invariance
![]() $N^*>_uM$
. On the other hand,
$N^*>_uM$
. On the other hand,
![]() $N'>_uN$
, then
$N'>_uN$
, then
![]() $N'>_uN_1$
and there is
$N'>_uN_1$
and there is
![]() $g:N^*\xrightarrow [N_1]{}N'$
. Let the image of g be
$g:N^*\xrightarrow [N_1]{}N'$
. Let the image of g be
![]() $N^{**}.$
$N^{**}.$
In the diagram below, we use dashed arrows to indicate isomorphisms. Solid arrows indicate
![]() $\leq $
.
$\leq $
.

Since
![]() $\tilde {f}\circ g^{-1}:N^{**}\cong _{M}N$
and
$\tilde {f}\circ g^{-1}:N^{**}\cong _{M}N$
and
![]() $M<_u N^{**},N\leq N'$
, we consider
$M<_u N^{**},N\leq N'$
, we consider
![]() $\tilde {f}\circ g^{-1}(p)\restriction N$
and
$\tilde {f}\circ g^{-1}(p)\restriction N$
and
![]() $p\restriction N$
.
$p\restriction N$
.
 $$ \begin{align*} \tilde{f}\circ g^{-1}(p)\restriction N&\geq[\tilde{f}\circ g^{-1}(p)]\restriction N_2\\ &=\tilde{f}([g^{-1}(p)]\restriction N_1)\restriction N_2\quad\text{as } \tilde{f}^{-1}[N_2]=N_1\\ &=\tilde{f}(p\restriction N_1)\restriction N_2\quad\text{as } g \text{ fixes } N_1\\ &=f(p\restriction N_1)\restriction N_2\quad\text{as } \tilde{f} \text{ extends } f\\ &=f(p\restriction N)\restriction N_2\quad\text{as } f^{-1}[N_2]=N_1\leq N\\ p\restriction N&\geq p\restriction N_2. \end{align*} $$
$$ \begin{align*} \tilde{f}\circ g^{-1}(p)\restriction N&\geq[\tilde{f}\circ g^{-1}(p)]\restriction N_2\\ &=\tilde{f}([g^{-1}(p)]\restriction N_1)\restriction N_2\quad\text{as } \tilde{f}^{-1}[N_2]=N_1\\ &=\tilde{f}(p\restriction N_1)\restriction N_2\quad\text{as } g \text{ fixes } N_1\\ &=f(p\restriction N_1)\restriction N_2\quad\text{as } \tilde{f} \text{ extends } f\\ &=f(p\restriction N)\restriction N_2\quad\text{as } f^{-1}[N_2]=N_1\leq N\\ p\restriction N&\geq p\restriction N_2. \end{align*} $$
Since
![]() $f(p\restriction N)\restriction N_2\neq p\restriction N_2$
,
$f(p\restriction N)\restriction N_2\neq p\restriction N_2$
,
![]() $\tilde {f}\circ g^{-1}(p)\restriction N\neq p\restriction N$
and we can take
$\tilde {f}\circ g^{-1}(p)\restriction N\neq p\restriction N$
and we can take
![]() $N_1':= N^{**}$
,
$N_1':= N^{**}$
,
![]() $N_2':= N$
,
$N_2':= N$
,
![]() $f':=\tilde {f}\circ g^{-1}$
in the statement of the lemma.
$f':=\tilde {f}\circ g^{-1}$
in the statement of the lemma.
Now we can prove a canonicity result for our frame. In order to apply Lemma 4.17, we will need to enlarge N to a universal extension in order to have more room. This procedure is absent in the original forward direction of Fact 4.15 but is similar to the backward direction (to get q below).
Proposition 4.18. Suppose there is an independence relation over the
![]() $(\mu ,\geq \chi )$
-limit models ordered by
$(\mu ,\geq \chi )$
-limit models ordered by
![]() $\leq _u$
satisfying invariance, monotonicity, local character
$\leq _u$
satisfying invariance, monotonicity, local character
![]() $\chi $
, uniqueness, and extension. Let
$\chi $
, uniqueness, and extension. Let
![]() $M<_u N$
be
$M<_u N$
be
![]() $(\mu ,\geq \chi )$
-limit models and
$(\mu ,\geq \chi )$
-limit models and
![]() $p\in \operatorname {gS}(N)$
. Then p is independent over M iff p does not
$p\in \operatorname {gS}(N)$
. Then p is independent over M iff p does not
![]() $\mu $
-fork over M.
$\mu $
-fork over M.
Proof Suppose p is independent over M. By assumption M is a
![]() $(\mu ,\delta )$
-limit for some regular
$(\mu ,\delta )$
-limit for some regular
![]() $\delta \in [\chi ,\mu ^+)$
. Resolve
$\delta \in [\chi ,\mu ^+)$
. Resolve
![]() $M=\bigcup _{i<\delta }M_i$
such that all
$M=\bigcup _{i<\delta }M_i$
such that all
![]() $M_i$
are also
$M_i$
are also
![]() $(\mu ,\delta )$
-limit. By local character,
$(\mu ,\delta )$
-limit. By local character,
![]() $p\restriction M$
is independent over
$p\restriction M$
is independent over
![]() $M_i$
for some
$M_i$
for some
![]() $i<\delta $
. Since the independence relation satisfies uniqueness and extension, by the proof of Corollary 4.8 it also satisfies transitivity. Therefore p is independent over
$i<\delta $
. Since the independence relation satisfies uniqueness and extension, by the proof of Corollary 4.8 it also satisfies transitivity. Therefore p is independent over
![]() $M_i$
. Let
$M_i$
. Let
![]() $N'>_uN$
. By extension, there is
$N'>_uN$
. By extension, there is
![]() $p'\in \operatorname {gS}(N')$
independent over
$p'\in \operatorname {gS}(N')$
independent over
![]() $M_i$
and
$M_i$
and
![]() $p'\supseteq p$
. Now suppose
$p'\supseteq p$
. Now suppose
![]() $p \ \mu $
-splits over
$p \ \mu $
-splits over
![]() $M_i$
, by Lemma 4.17
$M_i$
, by Lemma 4.17
![]() $p' \ \mu $
-splits over
$p' \ \mu $
-splits over
![]() $M_i$
with universal witnesses, contradicting Lemma 4.16 (where
$M_i$
with universal witnesses, contradicting Lemma 4.16 (where
![]() $\leq $
is replaced by
$\leq $
is replaced by
![]() $<_u$
where). As a result, p does not
$<_u$
where). As a result, p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_i$
. Since
$M_i$
. Since
![]() $M_i<_u M$
, p does not
$M_i<_u M$
, p does not
![]() $\mu $
-fork over M.
$\mu $
-fork over M.
Conversely suppose p does not
![]() $\mu $
-fork over M. By local character and monotonicity,
$\mu $
-fork over M. By local character and monotonicity,
![]() $p\restriction M$
is independent over M. By extension, obtain
$p\restriction M$
is independent over M. By extension, obtain
![]() $q\in \operatorname {gS}(N)$
independent over M and
$q\in \operatorname {gS}(N)$
independent over M and
![]() $q\supseteq p$
. From the forward direction, q does not
$q\supseteq p$
. From the forward direction, q does not
![]() $\mu $
-fork over M. By Proposition 4.5,
$\mu $
-fork over M. By Proposition 4.5,
![]() $p=q$
so invariance gives q independent over M.
$p=q$
so invariance gives q independent over M.
To conclude this section, we show that the existence of a frame similar to Corollary 4.13 is sufficient to obtain local character of nonsplitting. Continuity of
![]() $\mu $
-nonsplitting and
$\mu $
-nonsplitting and
![]() $\mu $
-tameness in Assumption 2.1 are not needed.
$\mu $
-tameness in Assumption 2.1 are not needed.
Proposition 4.19. Let
![]() $\delta <\mu ^+$
be regular. Suppose there is an independence relation over the
$\delta <\mu ^+$
be regular. Suppose there is an independence relation over the
![]() $(\mu ,\geq \delta )$
-limit models ordered by
$(\mu ,\geq \delta )$
-limit models ordered by
![]() $\leq _u$
satisfying invariance, monotonicity, local character
$\leq _u$
satisfying invariance, monotonicity, local character
![]() $\delta $
, uniqueness, and extension. Then
$\delta $
, uniqueness, and extension. Then
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $\delta $
-local character of
$\delta $
-local character of
![]() $\mu $
-nonsplitting.
$\mu $
-nonsplitting.
Proof Let
![]() $\langle M_i:i\leq \delta \rangle $
be u-increasing and continuous,
$\langle M_i:i\leq \delta \rangle $
be u-increasing and continuous,
![]() $p\in \operatorname {gS}(M_\delta )$
. There is
$p\in \operatorname {gS}(M_\delta )$
. There is
![]() $i<\delta $
such that p is independent over
$i<\delta $
such that p is independent over
![]() $M_i$
. By the forward direction of Proposition 4.18 (local character of nonsplitting is not used), p does not
$M_i$
. By the forward direction of Proposition 4.18 (local character of nonsplitting is not used), p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M_i$
.
$M_i$
.
5 Local symmetry
Tower analysis was used in [Reference VanDieren29, Theorem 3] to connect a notion of
![]() $\mu $
-symmetry and reduced towers. Combining with [Reference Grossberg, VanDieren and Villaveces17], superstability and
$\mu $
-symmetry and reduced towers. Combining with [Reference Grossberg, VanDieren and Villaveces17], superstability and
![]() $\mu $
-symmetry imply the uniqueness of limit models. VanDieren and Vasey [Reference VanDieren and Vasey31, Lemma 4.6] observed that a weaker form of
$\mu $
-symmetry imply the uniqueness of limit models. VanDieren and Vasey [Reference VanDieren and Vasey31, Lemma 4.6] observed that a weaker form of
![]() $\mu $
-symmetry is sufficient to deduce one direction of [Reference VanDieren29, Theorem 3], and enough superstability implies the weaker form of
$\mu $
-symmetry is sufficient to deduce one direction of [Reference VanDieren29, Theorem 3], and enough superstability implies the weaker form of
![]() $\mu $
-symmetry. Therefore enough superstability already implies the uniqueness of limit models [Reference VanDieren and Vasey31, Corollary 1.4]. Meanwhile, [Reference Boney and VanDieren10] localized the notion of
$\mu $
-symmetry. Therefore enough superstability already implies the uniqueness of limit models [Reference VanDieren and Vasey31, Corollary 1.4]. Meanwhile, [Reference Boney and VanDieren10] localized the notion of
![]() $\mu $
-symmetry and deduced the uniqueness of limit models of length
$\mu $
-symmetry and deduced the uniqueness of limit models of length
![]() $\geq \chi $
. We will imitate the above argument and replace the hypothesis of local symmetry by sufficient stability. As a corollary we will obtain symmetry property of nonforking. The uniqueness of limit models will be discussed in the next section.
$\geq \chi $
. We will imitate the above argument and replace the hypothesis of local symmetry by sufficient stability. As a corollary we will obtain symmetry property of nonforking. The uniqueness of limit models will be discussed in the next section.
The following is based on [Reference Boney and VanDieren10, Definition 10]. They restricted
![]() $M_0$
to be exactly
$M_0$
to be exactly
![]() $(\mu ,\delta )$
-limit over N but they should mean
$(\mu ,\delta )$
-limit over N but they should mean
![]() $(\mu ,\geq \delta )$
for the proofs to go through. We will use
$(\mu ,\geq \delta )$
for the proofs to go through. We will use
![]() $\delta :=\chi $
in this paper.
$\delta :=\chi $
in this paper.
Definition 5.1. Let
![]() $\delta <\mu ^+$
be a limit ordinal.
$\delta <\mu ^+$
be a limit ordinal.
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $(\mu ,\delta )$
-symmetry for
$(\mu ,\delta )$
-symmetry for
![]() $\mu $
-nonsplitting if for any
$\mu $
-nonsplitting if for any
![]() $M,M_0,N\in K_{\mu }$
, elements
$M,M_0,N\in K_{\mu }$
, elements
![]() $a,b$
with:
$a,b$
with:
-
1.
 $a\in M-M_0$
;
$a\in M-M_0$
; -
2.
 $M_0<_uM$
and
$M_0<_uM$
and
 $M_0$
is
$M_0$
is
 $(\mu ,\geq \delta )$
-limit over N;
$(\mu ,\geq \delta )$
-limit over N; -
3.
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-split over N;
$\mu $
-split over N; -
4.
 $\operatorname {gtp}(b/M)$
does not
$\operatorname {gtp}(b/M)$
does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
,
$M_0$
,
then there is
![]() $M^b\in K_{\mu }$
universal over
$M^b\in K_{\mu }$
universal over
![]() $M_0$
and containing b such that
$M_0$
and containing b such that
![]() $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
![]() $\mu $
-split over N. We will abbreviate
$\mu $
-split over N. We will abbreviate
![]() $(\mu ,\delta )$
-symmetry for
$(\mu ,\delta )$
-symmetry for
![]() $\mu $
-nonsplitting as
$\mu $
-nonsplitting as
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
Now we localize the hierarchy of symmetry properties in [Reference VanDieren and Vasey31, Definition 4.3]. The first two items will be important in our improvement of [Reference Boney and VanDieren10].
Definition 5.2. Let
![]() $\delta <\mu ^+$
be a limit ordinal. In the following items, we always let
$\delta <\mu ^+$
be a limit ordinal. In the following items, we always let
![]() $a\in M-M_0$
,
$a\in M-M_0$
,
![]() $M_0<_uM$
,
$M_0<_uM$
,
![]() $M_0$
be
$M_0$
be
![]() $(\mu ,\geq \delta )$
-limit over N and b be an element. In the conclusion,
$(\mu ,\geq \delta )$
-limit over N and b be an element. In the conclusion,
![]() $M^b\in K_{\mu }$
universal over
$M^b\in K_{\mu }$
universal over
![]() $M_0$
and containing b is guaranteed to exist.
$M_0$
and containing b is guaranteed to exist.
-
1.
 $\mathbf {K}$
has uniform
$\mathbf {K}$
has uniform
 $(\mu ,\delta )$
-symmetry: If
$(\mu ,\delta )$
-symmetry: If
 $\operatorname {gtp}(b/M)$
does not
$\operatorname {gtp}(b/M)$
does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
,
$M_0$
,
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
, then
$(N,M_0)$
, then
 $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
.
$(N,M_0)$
. -
2.
 $\mathbf {K}$
has weak uniform
$\mathbf {K}$
has weak uniform
 $(\mu ,\delta )$
-symmetry: If
$(\mu ,\delta )$
-symmetry: If
 $\operatorname {gtp}(b/M)$
does not
$\operatorname {gtp}(b/M)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
,
$M_0$
,
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
, then
$(N,M_0)$
, then
 $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
.
$(N,M_0)$
. -
3.
 $\mathbf {K}$
has nonuniform
$\mathbf {K}$
has nonuniform
 $(\mu ,\delta )$
-symmetry: If
$(\mu ,\delta )$
-symmetry: If
 $\operatorname {gtp}(b/M)$
does not
$\operatorname {gtp}(b/M)$
does not
 $\mu $
-split over
$\mu $
-split over
 $M_0$
,
$M_0$
,
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
, then
$M_0$
, then
 $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
.
$M_0$
. -
4.
 $\mathbf {K}$
has weak nonuniform
$\mathbf {K}$
has weak nonuniform
 $(\mu ,\delta )$
-symmetry: If
$(\mu ,\delta )$
-symmetry: If
 $\operatorname {gtp}(b/M)$
does not
$\operatorname {gtp}(b/M)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
,
$M_0$
,
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
, then
$M_0$
, then
 $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
.
$M_0$
.
The following results generalize [Reference VanDieren and Vasey31, Section 4] which assumes superstability and works with full symmetry properties.
Proposition 5.3. Let
![]() $\delta <\mu ^+$
be a limit ordinal.
$\delta <\mu ^+$
be a limit ordinal.
![]() $(\mu ,\delta )$
-symmetry is equivalent to uniform
$(\mu ,\delta )$
-symmetry is equivalent to uniform
![]() $(\mu ,\delta )$
-symmetry. Both imply nonuniform
$(\mu ,\delta )$
-symmetry. Both imply nonuniform
![]() $(\mu ,\delta )$
-symmetry and weak uniform
$(\mu ,\delta )$
-symmetry and weak uniform
![]() $(\mu ,\delta )$
-symmetry. Nonuniform
$(\mu ,\delta )$
-symmetry. Nonuniform
![]() $(\mu ,\delta )$
-symmetry implies weak nonuniform
$(\mu ,\delta )$
-symmetry implies weak nonuniform
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
Proof In the definition of the symmetry properties, we always have
![]() $N<_uM_0$
, so the following are equivalent:
$N<_uM_0$
, so the following are equivalent:
-
•
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
;
$(N,M_0)$
; -
•
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-split over N.
$\mu $
-split over N.
Similarly, the following are equivalent:
-
•
 $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
;
$(N,M_0)$
; -
•
 $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
 $\mu $
-split over N.
$\mu $
-split over N.
Therefore,
![]() $(\mu ,\delta )$
-symmetry is equivalent to uniform
$(\mu ,\delta )$
-symmetry is equivalent to uniform
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
Uniform
![]() $(\mu ,\delta )$
-symmetry implies weak uniform
$(\mu ,\delta )$
-symmetry implies weak uniform
![]() $(\mu ,\delta )$
-symmetry because nonforking over
$(\mu ,\delta )$
-symmetry because nonforking over
![]() $M_0$
is a stronger assumption than nonsplitting over
$M_0$
is a stronger assumption than nonsplitting over
![]() $M_0$
. Uniform
$M_0$
. Uniform
![]() $(\mu ,\delta )$
-symmetry implies nonuniform
$(\mu ,\delta )$
-symmetry implies nonuniform
![]() $(\mu ,\delta )$
-symmetry because the latter does not require the witness to nonforking be the same, so its conclusion is weaker. Nonuniform
$(\mu ,\delta )$
-symmetry because the latter does not require the witness to nonforking be the same, so its conclusion is weaker. Nonuniform
![]() $(\mu ,\delta )$
-symmetry implies weak nonuniform
$(\mu ,\delta )$
-symmetry implies weak nonuniform
![]() $(\mu ,\delta )$
-symmetry because nonforking over
$(\mu ,\delta )$
-symmetry because nonforking over
![]() $M_0$
is a stronger assumption than nonsplitting over
$M_0$
is a stronger assumption than nonsplitting over
![]() $M_0$
.
$M_0$
.
The following result modifies the proof of [Reference Boney and VanDieren10] which involves a lot of tower analysis. We will only mention the modifications and refer the readers to the original proof.
Proposition 5.4. Let
![]() $\delta <\mu ^+$
be a limit ordinal. If
$\delta <\mu ^+$
be a limit ordinal. If
![]() $\delta \geq \chi $
, then weak uniform
$\delta \geq \chi $
, then weak uniform
![]() $(\mu ,\delta )$
-symmetry implies uniform
$(\mu ,\delta )$
-symmetry implies uniform
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
Proof sketch
[Reference Boney and VanDieren10, Theorem 18 and Proposition 19] establish that
![]() $(\mu ,\delta )$
-symmetry is equivalent to continuity of reduced towers at
$(\mu ,\delta )$
-symmetry is equivalent to continuity of reduced towers at
![]() $\geq \delta $
. We will show that the backward direction only requires weak uniform
$\geq \delta $
. We will show that the backward direction only requires weak uniform
![]() $(\mu ,\delta )$
-symmetry. Then using the equivalence twice we deduce that weak uniform
$(\mu ,\delta )$
-symmetry. Then using the equivalence twice we deduce that weak uniform
![]() $(\mu ,\delta )$
-symmetry implies
$(\mu ,\delta )$
-symmetry implies
![]() $(\mu ,\delta )$
-symmetry. By the previous proposition, it is equivalent to uniform
$(\mu ,\delta )$
-symmetry. By the previous proposition, it is equivalent to uniform
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
There are three places in [Reference Boney and VanDieren10, Theorem 18] which use
![]() $(\mu ,\delta )$
-symmetry. In the first two paragraphs of page 11:
$(\mu ,\delta )$
-symmetry. In the first two paragraphs of page 11:
-
1. By
 $\chi $
-local character, there is a successor
$\chi $
-local character, there is a successor
 $i^*<\delta $
such that
$i^*<\delta $
such that
 $\operatorname {gtp}(b/M_\delta ^\delta )$
does not
$\operatorname {gtp}(b/M_\delta ^\delta )$
does not
 $\mu $
-split over
$\mu $
-split over
 $M_{i^*}^{i^*}$
.
$M_{i^*}^{i^*}$
. -
2. For any
 $j<\delta $
,
$j<\delta $
,
 $M_\delta ^\delta $
is universal over
$M_\delta ^\delta $
is universal over
 $M_{j}^{j}$
.
$M_{j}^{j}$
. -
3. For any
 $j<\delta $
,
$j<\delta $
,
 $\operatorname {gtp}(a_{j}/M_{j}^{j})$
does not
$\operatorname {gtp}(a_{j}/M_{j}^{j})$
does not
 $\mu $
-split over
$\mu $
-split over
 $N_{j}$
.
$N_{j}$
. -
4. For any successor
 $j<\delta $
,
$j<\delta $
,
 $M_j^j$
is
$M_j^j$
is
 $(\mu ,\geq \delta )$
-limit over
$(\mu ,\geq \delta )$
-limit over
 $M_{j-1}^{j-1}$
and over
$M_{j-1}^{j-1}$
and over
 $N_j$
.
$N_j$
.
Let
![]() $j^*:= i^*+1$
which is still a successor ordinal less than
$j^*:= i^*+1$
which is still a successor ordinal less than
![]() $\delta $
. Combining (1) and (4), we have
$\delta $
. Combining (1) and (4), we have
![]() $\operatorname {gtp}(b/M_\delta ^\delta )$
does not
$\operatorname {gtp}(b/M_\delta ^\delta )$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_{j^*}^{j^*}$
. Combining (3) and (4),
$M_{j^*}^{j^*}$
. Combining (3) and (4),
![]() $\operatorname {gtp}(a_{j^*}/M_{j^*}^{j^*})$
does not
$\operatorname {gtp}(a_{j^*}/M_{j^*}^{j^*})$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_{j^*}^{j^*})$
. Moreover, (2) gives
$M_{j^*}^{j^*})$
. Moreover, (2) gives
![]() $M_\delta ^\delta $
is universal over
$M_\delta ^\delta $
is universal over
![]() $M_{j^*}^{j^*}$
. Together with (4) and weak uniform
$M_{j^*}^{j^*}$
. Together with (4) and weak uniform
![]() $(\mu ,\delta )$
-symmetry, we can find
$(\mu ,\delta )$
-symmetry, we can find
![]() $M^b \ (\mu ,\geq \delta )$
-limit over
$M^b \ (\mu ,\geq \delta )$
-limit over
![]() $M_{j^*}^{j^*}$
and containing b such that
$M_{j^*}^{j^*}$
and containing b such that
![]() $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N_{j^*},M_{j^*}^{j^*})$
. In other words,
$(N_{j^*},M_{j^*}^{j^*})$
. In other words,
![]() $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N_{j^*}$
and so the original argument goes through with
$N_{j^*}$
and so the original argument goes through with
![]() $i^*$
replaced by
$i^*$
replaced by
![]() $j^*$
.
$j^*$
.
In “Case 2” on page 12:
-
a.
 $\operatorname {gtp}(b/\bigcup _{l<\alpha }M_l^l)$
does not
$\operatorname {gtp}(b/\bigcup _{l<\alpha }M_l^l)$
does not
 $\mu $
-split over
$\mu $
-split over
 $M_{i^*}^{i^*}$
.
$M_{i^*}^{i^*}$
. -
b.
 $i^*+2\leq k<\alpha $
and
$i^*+2\leq k<\alpha $
and
 $\operatorname {gtp}(a_k/M_k^{k+1})$
does not
$\operatorname {gtp}(a_k/M_k^{k+1})$
does not
 $\mu $
-split over
$\mu $
-split over
 $N_k$
.
$N_k$
. -
c.
 $M_k^{k+1}$
is universal over
$M_k^{k+1}$
is universal over
 $M_{i^*}^{i^*}$
.
$M_{i^*}^{i^*}$
. -
d.
 $\bigcup _{l<\alpha }M_l^l$
is universal over
$\bigcup _{l<\alpha }M_l^l$
is universal over
 $M_k^{k+1}$
.
$M_k^{k+1}$
.
 $M_k^{k+1}$
is
$M_k^{k+1}$
is
 $(\mu ,\geq \delta )$
-limit over
$(\mu ,\geq \delta )$
-limit over
 $N_k$
.
$N_k$
.
Combining (a) and (c),
![]() $\operatorname {gtp}(b/\bigcup _{l<\alpha }M_l^l)$
does not
$\operatorname {gtp}(b/\bigcup _{l<\alpha }M_l^l)$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_k^{k+1}$
. (b) gives
$M_k^{k+1}$
. (b) gives
![]() $\operatorname {gtp}(a_k/M_k^{k+1})$
does not
$\operatorname {gtp}(a_k/M_k^{k+1})$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N_k,M_k^{k+1})$
. Together with (d) and weak uniform
$(N_k,M_k^{k+1})$
. Together with (d) and weak uniform
![]() $(\mu ,\delta )$
-symmetry, we can find
$(\mu ,\delta )$
-symmetry, we can find
![]() $M^b_k \ (\mu ,\geq \delta )$
-limit over
$M^b_k \ (\mu ,\geq \delta )$
-limit over
![]() $M_{k}^{k+1}$
and containing b such that
$M_{k}^{k+1}$
and containing b such that
![]() $\operatorname {gtp}(a_k/M^b_k)$
does not
$\operatorname {gtp}(a_k/M^b_k)$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N_{k},M_{k}^{k+1})$
so the proof goes through (we do not change index this time).
$(N_{k},M_{k}^{k+1})$
so the proof goes through (we do not change index this time).
Before “Case 1” on page 11, they refer the successor case to the original proof of [Reference VanDieren29, Theorem 3] which also uses
![]() $(\mu ,\delta )$
-symmetry. But the idea from the previous case applies equally.
$(\mu ,\delta )$
-symmetry. But the idea from the previous case applies equally.
In [Reference Vasey35, Corollary 2.18], it was shown that under superstability, weak nonuniform
![]() $\mu $
-symmetry implies weak uniform
$\mu $
-symmetry implies weak uniform
![]() $\mu $
-symmetry. We generalize this as the following.
$\mu $
-symmetry. We generalize this as the following.
Proposition 5.5. Let
![]() $\delta <\mu ^+$
be a limit ordinal. Weak nonuniform
$\delta <\mu ^+$
be a limit ordinal. Weak nonuniform
![]() $(\mu ,\delta )$
-symmetry implies weak uniform
$(\mu ,\delta )$
-symmetry implies weak uniform
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
Proof Using the notation in Definition 5.2, we assume
![]() $\operatorname {gtp}(b/M)$
does not
$\operatorname {gtp}(b/M)$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
and
$M_0$
and
![]() $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N,M_0)$
. By weak nonuniform
$(N,M_0)$
. By weak nonuniform
![]() $(\mu ,\delta )$
-symmetry, we can find
$(\mu ,\delta )$
-symmetry, we can find
![]() $M^b$
such that
$M^b$
such that
![]() $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
. Since
$M_0$
. Since
![]() $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N,M_0)$
, by extension of nonsplitting (Proposition 3.12), there is
$(N,M_0)$
, by extension of nonsplitting (Proposition 3.12), there is
![]() $a'$
such that
$a'$
such that
![]() $\operatorname {gtp}(a/M_0)=\operatorname {gtp}(a'/M_0)$
and
$\operatorname {gtp}(a/M_0)=\operatorname {gtp}(a'/M_0)$
and
![]() $\operatorname {gtp}(a'/M^b)$
does not
$\operatorname {gtp}(a'/M^b)$
does not
![]() $\mu $
-split over N. Now both
$\mu $
-split over N. Now both
![]() $\operatorname {gtp}(a/M^b)$
and
$\operatorname {gtp}(a/M^b)$
and
![]() $\operatorname {gtp}(a'/M^b)$
do not
$\operatorname {gtp}(a'/M^b)$
do not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
and they agree on the restriction of
$M_0$
and they agree on the restriction of
![]() $M_0$
. By uniqueness of nonforking (Proposition 4.5),
$M_0$
. By uniqueness of nonforking (Proposition 4.5),
![]() $\operatorname {gtp}(a/M^b)=\operatorname {gtp}(a'/M^b)$
and hence
$\operatorname {gtp}(a/M^b)=\operatorname {gtp}(a'/M^b)$
and hence
![]() $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
![]() $\mu $
-split over N. In other words, it does not
$\mu $
-split over N. In other words, it does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N,M_0)$
as desired.
$(N,M_0)$
as desired.
Corollary 5.6. The following are equivalent:
-
0.
 $(\mu ,\chi )$
-symmetry for
$(\mu ,\chi )$
-symmetry for
 $\mu $
-nonsplitting.
$\mu $
-nonsplitting. -
1. Uniform
 $(\mu ,\chi )$
-symmetry.
$(\mu ,\chi )$
-symmetry. -
2. Weak uniform
 $(\mu ,\chi )$
-symmetry.
$(\mu ,\chi )$
-symmetry. -
3. Nonuniform
 $(\mu ,\chi )$
-symmetry.
$(\mu ,\chi )$
-symmetry. -
4. Weak nonuniform
 $(\mu ,\chi )$
-symmetry.
$(\mu ,\chi )$
-symmetry.
Proof By Proposition 5.3, (0) and (1) are equivalent, (1) implies (2) and (3) while (3) implies (4). By Proposition 5.4 (this is where we need
![]() $\chi $
instead of a general
$\chi $
instead of a general
![]() $\delta $
), (2) implies (1). By Proposition 5.5, (4) implies (2).
$\delta $
), (2) implies (1). By Proposition 5.5, (4) implies (2).
The following adapts [Reference VanDieren and Vasey31, Lemma 5.6] and fills in some gaps. In particular we need
![]() $\mu $
-tameness (in Assumption 2.1) and stability in
$\mu $
-tameness (in Assumption 2.1) and stability in
![]() $\Vert N_\alpha \Vert $
for the proof to go through. It is not clear how to remove
$\Vert N_\alpha \Vert $
for the proof to go through. It is not clear how to remove
![]() $\mu $
-tameness which they do not assume.
$\mu $
-tameness which they do not assume.
Lemma 5.7. Let
![]() $M_0\in K_{\mu }$
,
$M_0\in K_{\mu }$
,
![]() $N_\alpha \in K_{\geq \mu }$
with
$N_\alpha \in K_{\geq \mu }$
with
![]() $M_0\leq N_\alpha $
,
$M_0\leq N_\alpha $
,
![]() $b,b_\beta \in |N_\alpha |$
,
$b,b_\beta \in |N_\alpha |$
,
![]() $a_\alpha $
be an element. If
$a_\alpha $
be an element. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $\Vert N_\alpha \Vert $
,
$\Vert N_\alpha \Vert $
,
![]() $\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
$\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
and
$M_0$
and
![]() $\operatorname {gtp}(b/M_0)=\operatorname {gtp}(b_\beta /M_0)$
, then
$\operatorname {gtp}(b/M_0)=\operatorname {gtp}(b_\beta /M_0)$
, then
![]() $\operatorname {gtp}(a_\alpha b/M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$
.
$\operatorname {gtp}(a_\alpha b/M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$
.
Proof Let
![]() $M^*<_u M_0$
witness that
$M^*<_u M_0$
witness that
![]() $\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
$\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(M^*,M_0)$
. By stability, extend
$(M^*,M_0)$
. By stability, extend
![]() $N_\alpha $
to
$N_\alpha $
to
![]() $N^*>_u N_\alpha $
such that
$N^*>_u N_\alpha $
such that
![]() $\operatorname {gtp}(a_\alpha /N^*)$
does not
$\operatorname {gtp}(a_\alpha /N^*)$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M^*$
. As
$M^*$
. As
![]() $\operatorname {gtp}(b/M_0)=\operatorname {gtp}(b_\beta /M_0)$
, there is
$\operatorname {gtp}(b/M_0)=\operatorname {gtp}(b_\beta /M_0)$
, there is
![]() $f:N_\alpha \xrightarrow [M_0]{N^*}$
such that
$f:N_\alpha \xrightarrow [M_0]{N^*}$
such that
![]() $f(b)=b_\beta $
. As
$f(b)=b_\beta $
. As
![]() $\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
$\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $M^*$
, by Proposition 3.4
$M^*$
, by Proposition 3.4
![]() $\operatorname {gtp}(f(a_\alpha )/f(N_\alpha ))=\operatorname {gtp}(a_\alpha /f(N_\alpha ))$
. Hence there is
$\operatorname {gtp}(f(a_\alpha )/f(N_\alpha ))=\operatorname {gtp}(a_\alpha /f(N_\alpha ))$
. Hence there is
![]() $g\in \operatorname {Aut}_{f(N_\alpha )}\mathfrak {C}$
such that
$g\in \operatorname {Aut}_{f(N_\alpha )}\mathfrak {C}$
such that
![]() $g(f(a_\alpha ))=a_\alpha $
. Then
$g(f(a_\alpha ))=a_\alpha $
. Then
Remark 5.8. By swapping the dummy variables, we have the following formulation: Let
![]() $M_0\in K_{\mu }$
,
$M_0\in K_{\mu }$
,
![]() $N_\beta '\in K_{\geq \mu }$
with
$N_\beta '\in K_{\geq \mu }$
with
![]() $M_0\leq N_\beta '$
,
$M_0\leq N_\beta '$
,
![]() $a,a_\alpha \in |N_\beta '|$
,
$a,a_\alpha \in |N_\beta '|$
,
![]() $b_\beta $
be an element. If
$b_\beta $
be an element. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $\Vert N_\beta ' \Vert $
,
$\Vert N_\beta ' \Vert $
,
![]() $\operatorname {gtp}(b_\beta /N_\beta ')$
does not
$\operatorname {gtp}(b_\beta /N_\beta ')$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
and
$M_0$
and
![]() $\operatorname {gtp}(a/M_0)=\operatorname {gtp}(a_\alpha /M_0)$
, then
$\operatorname {gtp}(a/M_0)=\operatorname {gtp}(a_\alpha /M_0)$
, then
![]() $\operatorname {gtp}(ab_\beta /M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$
.
$\operatorname {gtp}(ab_\beta /M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$
.
The following adapts [Reference VanDieren and Vasey31, Lemma 5.7] which assumes superstability in
![]() $[\mu ,\lambda )$
. When we write the
$[\mu ,\lambda )$
. When we write the
![]() $\mu $
-order property, we mean tuples that witness order property have length
$\mu $
-order property, we mean tuples that witness order property have length
![]() $\mu $
.
$\mu $
.
Proposition 5.9. Let
![]() $\lambda \geq \mu $
be a cardinal. If
$\lambda \geq \mu $
be a cardinal. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda )$
and fails
$[\mu ,\lambda )$
and fails
![]() $(\mu ,\chi )$
-symmetry, then it has the
$(\mu ,\chi )$
-symmetry, then it has the
![]() $\mu $
-order property of length
$\mu $
-order property of length
![]() $\lambda $
.
$\lambda $
.
Proof By Corollary 5.6(2)
![]() $\Rightarrow $
(0),
$\Rightarrow $
(0),
![]() $\mathbf {K}$
fails weak uniform
$\mathbf {K}$
fails weak uniform
![]() $(\mu ,\chi )$
-symmetry. So there are
$(\mu ,\chi )$
-symmetry. So there are
![]() $N,M_0,M\in K_{\mu }$
and elements
$N,M_0,M\in K_{\mu }$
and elements
![]() $a,b$
such that:
$a,b$
such that:
-
•
 $a\in M-M_0$
,
$a\in M-M_0$
,
 $M_0<_uM$
and
$M_0<_uM$
and
 $M_0$
is
$M_0$
is
 $(\mu ,\geq \chi )$
-limit over N.
$(\mu ,\geq \chi )$
-limit over N. -
•
 $\operatorname {gtp}(b/M)$
does not
$\operatorname {gtp}(b/M)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
.
$M_0$
. -
•
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
.
$(N,M_0)$
. -
• There is no
 $M^b\in K_{\mu }$
universal over
$M^b\in K_{\mu }$
universal over
 $M_0$
containing b such that
$M_0$
containing b such that
 $\operatorname {gtp}(a/M^b)$
does not
$\operatorname {gtp}(a/M^b)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
.
$(N,M_0)$
.
Build
![]() $\langle a_\alpha ,b_\alpha ,N_\alpha ,N_\alpha '\rangle $
increasing and continuous such that for
$\langle a_\alpha ,b_\alpha ,N_\alpha ,N_\alpha '\rangle $
increasing and continuous such that for
![]() $\alpha <\lambda $
:
$\alpha <\lambda $
:
-
1.
 $N_\alpha ,N_\alpha '\in K_{\mu +|\alpha |}$
;
$N_\alpha ,N_\alpha '\in K_{\mu +|\alpha |}$
; -
2.
 $b\in |N_0|$
and
$b\in |N_0|$
and
 $N_0$
is universal over M;
$N_0$
is universal over M; -
3.
 $N_\alpha <_u N_\alpha '<_uN_{\alpha +1}$
;
$N_\alpha <_u N_\alpha '<_uN_{\alpha +1}$
; -
4.
 $a_\alpha \in |N_\alpha '|$
and
$a_\alpha \in |N_\alpha '|$
and
 $\operatorname {gtp}(a_\alpha /M_0)=\operatorname {gtp}(a/M_0)$
;
$\operatorname {gtp}(a_\alpha /M_0)=\operatorname {gtp}(a/M_0)$
; -
5.
 $b_\alpha \in |N_{\alpha +1}|$
and
$b_\alpha \in |N_{\alpha +1}|$
and
 $\operatorname {gtp}(b_\alpha /M)=\operatorname {gtp}(b/M)$
;
$\operatorname {gtp}(b_\alpha /M)=\operatorname {gtp}(b/M)$
; -
6.
 $\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
$\operatorname {gtp}(a_\alpha /N_\alpha )$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $(N,M_0)$
;
$(N,M_0)$
; -
7.
 $\operatorname {gtp}(b_\alpha /N_\alpha ')$
does not
$\operatorname {gtp}(b_\alpha /N_\alpha ')$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
.
$M_0$
.
![]() $N_0$
is specified in (2). We specify the successor step: suppose
$N_0$
is specified in (2). We specify the successor step: suppose
![]() $N_\alpha $
has been constructed, by Corollary 4.3 there is
$N_\alpha $
has been constructed, by Corollary 4.3 there is
![]() $a_\alpha $
such that
$a_\alpha $
such that
![]() $\operatorname {gtp}(a_\alpha /N_\alpha )$
extends
$\operatorname {gtp}(a_\alpha /N_\alpha )$
extends
![]() $\operatorname {gtp}(a/M_0)$
and does not
$\operatorname {gtp}(a/M_0)$
and does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N,M_0)$
. Build any
$(N,M_0)$
. Build any
![]() $N_\alpha '$
universal over
$N_\alpha '$
universal over
![]() $N_\alpha $
containing
$N_\alpha $
containing
![]() $a_\alpha $
. By Proposition 4.2 again, there is
$a_\alpha $
. By Proposition 4.2 again, there is
![]() $b_\alpha $
such that
$b_\alpha $
such that
![]() $\operatorname {gtp}(b_\alpha /N_\alpha ')$
extends
$\operatorname {gtp}(b_\alpha /N_\alpha ')$
extends
![]() $\operatorname {gtp}(b/M)$
and does not
$\operatorname {gtp}(b/M)$
and does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_0$
. Build
$M_0$
. Build
![]() $N_{\alpha +1}$
universal over
$N_{\alpha +1}$
universal over
![]() $N_\alpha '$
containing
$N_\alpha '$
containing
![]() $b_\alpha $
. Notice that stability is used to guarantee the existence of
$b_\alpha $
. Notice that stability is used to guarantee the existence of
![]() $N_\alpha ,N_\alpha '$
and the extension of types.
$N_\alpha ,N_\alpha '$
and the extension of types.
After the construction, we have the following properties for
![]() $\alpha ,\beta <\lambda $
:
$\alpha ,\beta <\lambda $
:
-
a.
 $\operatorname {gtp}(a_\alpha b/M_0)\neq \operatorname {gtp}(ab/M_0)$
;
$\operatorname {gtp}(a_\alpha b/M_0)\neq \operatorname {gtp}(ab/M_0)$
; -
b.
 $\operatorname {gtp}(ab_\beta /M_0)=\operatorname {gtp}(ab/M_0)$
;
$\operatorname {gtp}(ab_\beta /M_0)=\operatorname {gtp}(ab/M_0)$
; -
c. If
 $\beta <\alpha $
,
$\beta <\alpha $
,
 $\operatorname {gtp}(ab/M_0)\neq \operatorname {gtp}(a_\alpha b_\beta /M_0)$
;
$\operatorname {gtp}(ab/M_0)\neq \operatorname {gtp}(a_\alpha b_\beta /M_0)$
; -
d. If
 $\beta \geq \alpha $
,
$\beta \geq \alpha $
,
 $\operatorname {gtp}(ab/M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$
.
$\operatorname {gtp}(ab/M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$
.
Suppose (a) is false. By invariance and the choice of
![]() $a,b,M_0,N$
there is no
$a,b,M_0,N$
there is no
![]() $M'\in K_{\mu }$
universal over
$M'\in K_{\mu }$
universal over
![]() $M_0$
containing b such that
$M_0$
containing b such that
![]() $\operatorname {gtp}(a_\alpha /M')$
does not
$\operatorname {gtp}(a_\alpha /M')$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $(N,M_0)$
. This contradicts
$(N,M_0)$
. This contradicts
![]() $M':= N_\alpha $
and item (6) in the construction. (b) is true because of item (5) of the construction and
$M':= N_\alpha $
and item (6) in the construction. (b) is true because of item (5) of the construction and
![]() $a\in |M|$
. For (c), items (5), (6) and Lemma 5.7 (with the exact same notations) imply
$a\in |M|$
. For (c), items (5), (6) and Lemma 5.7 (with the exact same notations) imply
![]() $\operatorname {gtp}(a_\alpha b_\beta /M_0)=\operatorname {gtp}(a_\alpha b/M_0)$
which is not equal to
$\operatorname {gtp}(a_\alpha b_\beta /M_0)=\operatorname {gtp}(a_\alpha b/M_0)$
which is not equal to
![]() $\operatorname {gtp}(ab/M_0)$
by (a). For (d), items (4), (7) and Remark 5.8 imply
$\operatorname {gtp}(ab/M_0)$
by (a). For (d), items (4), (7) and Remark 5.8 imply
![]() $\operatorname {gtp}(a_\alpha b_\beta /M_0)=\operatorname {gtp}(ab_\beta /M_0)$
which is equal to
$\operatorname {gtp}(a_\alpha b_\beta /M_0)=\operatorname {gtp}(ab_\beta /M_0)$
which is equal to
![]() $\operatorname {gtp}(ab/M_0)$
by (b).
$\operatorname {gtp}(ab/M_0)$
by (b).
To finish the proof, let d enumerate
![]() $M_0$
, and for
$M_0$
, and for
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $c_\alpha := a_\alpha b_\alpha d$
. By (c) and (d) above,
$c_\alpha := a_\alpha b_\alpha d$
. By (c) and (d) above,
![]() $\langle c_\alpha :\alpha <\lambda \rangle $
witnesses the
$\langle c_\alpha :\alpha <\lambda \rangle $
witnesses the
![]() $\mu $
-order property of length
$\mu $
-order property of length
![]() $\lambda $
.
$\lambda $
.
Remark 5.10. When proving (d), we used Remark 5.8 which requires
![]() $\operatorname {gtp}(b_\beta /N_\beta ')$
nonforking over
$\operatorname {gtp}(b_\beta /N_\beta ')$
nonforking over
![]() $M_0$
, and this is from extending
$M_0$
, and this is from extending
![]() $\operatorname {gtp}(b/M)$
nonforking over
$\operatorname {gtp}(b/M)$
nonforking over
![]() $M_0$
. This called for the failure of weak uniform
$M_0$
. This called for the failure of weak uniform
![]() $(\mu ,\chi )$
-symmetry instead of just
$(\mu ,\chi )$
-symmetry instead of just
![]() $(\mu ,\chi )$
-symmetry. (In the original proof, they claimed the same for (c) in place of (d), which should be a typo.)
$(\mu ,\chi )$
-symmetry. (In the original proof, they claimed the same for (c) in place of (d), which should be a typo.)
Question 5.11. Is it possible to weaken the stability assumption in Proposition 5.9?
Fact 5.12. For any infinite cardinal
![]() $\lambda $
,
$\lambda $
,
![]() $h(\lambda ):=\beth _{(2^{\lambda })^+}$
. When we write the
$h(\lambda ):=\beth _{(2^{\lambda })^+}$
. When we write the
![]() $\mu $
-stable, we mean stability of tuples of length
$\mu $
-stable, we mean stability of tuples of length
![]() $\mu $
.
$\mu $
.
-
1. [Reference Shelah23, Claim 4.6] If
 $\mathbf {K}$
does not have the
$\mathbf {K}$
does not have the
 $\mu $
-order property, then there is
$\mu $
-order property, then there is
 $\lambda <h(\mu )$
such that
$\lambda <h(\mu )$
such that
 $\mathbf {K}$
does not have the
$\mathbf {K}$
does not have the
 $\mu $
-order property of length
$\mu $
-order property of length
 $\lambda $
.
$\lambda $
. -
2. [Reference Boney, Grossberg, Kolesnikov and Vasey7, Fact 5.13] If
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-stable (in some cardinal
$\mu $
-stable (in some cardinal
 $\geq \mu $
), then it does not have the
$\geq \mu $
), then it does not have the
 $\mu $
-order property.
$\mu $
-order property. -
3. If
 $\mathbf {K}$
is stable in some
$\mathbf {K}$
is stable in some
 $\lambda =\lambda ^\mu $
, then
$\lambda =\lambda ^\mu $
, then
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\mu $
-stable in
$\mu $
-stable in
 $\lambda $
.
$\lambda $
. -
4. [Reference Grossberg and VanDieren16, Corollary 6.4] If
 $\mathbf {K}$
is stable and tame in
$\mathbf {K}$
is stable and tame in
 $\mu $
(these are in Assumption 2.1), then it is stable in all
$\mu $
(these are in Assumption 2.1), then it is stable in all
 $\lambda =\lambda ^\mu $
. In particular it is stable in
$\lambda =\lambda ^\mu $
. In particular it is stable in
 $2^\mu $
.
$2^\mu $
. -
5. For some
 $\lambda <h(\mu )$
,
$\lambda <h(\mu )$
,
 $\mathbf {K}$
does not have the
$\mathbf {K}$
does not have the
 $\mu $
-order property of length
$\mu $
-order property of length
 $\lambda $
.
$\lambda $
.
Proof For (1) and (2), see also [Reference Leung20, Proposition 3.4] for a proof sketch. (3) is an immediate corollary of [Reference Boney5, Theorem 3.1], see [Reference Leung20, Theorem 2.1] for a proof. We show (5): by (4)
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $2^\mu $
. By (3) it is
$2^\mu $
. By (3) it is
![]() $\mu $
-stable in
$\mu $
-stable in
![]() $2^\mu $
. Combining with (2) and (1) gives the conclusion.
$2^\mu $
. Combining with (2) and (1) gives the conclusion.
Corollary 5.13. There is
![]() $\lambda <h(\mu )$
such that if
$\lambda <h(\mu )$
such that if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda )$
, then:
$[\mu ,\lambda )$
, then:
-
1.
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $(\mu ,\chi )$
-symmetry;
$(\mu ,\chi )$
-symmetry; -
2. the frame in Corollary 4.13 satisfies symmetry.
Proof
-
1. By Fact 5.12(5), there is
 $\lambda <h(\mu )$
such that
$\lambda <h(\mu )$
such that
 $\mathbf {K}$
does not have the
$\mathbf {K}$
does not have the
 $\mu $
-order property of length
$\mu $
-order property of length
 $\lambda $
. By the contrapositive of Proposition 5.9,
$\lambda $
. By the contrapositive of Proposition 5.9,
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $(\mu ,\chi )$
-symmetry.
$(\mu ,\chi )$
-symmetry. -
2. By (1) and Proposition 5.3,
 $\mathbf {K}$
has weak nonuniform
$\mathbf {K}$
has weak nonuniform
 $(\mu ,\chi )$
-symmetry. Compared to symmetry in a good frame, weak nonuniform
$(\mu ,\chi )$
-symmetry. Compared to symmetry in a good frame, weak nonuniform
 $(\mu ,\chi )$
-symmetry has the extra assumption that
$(\mu ,\chi )$
-symmetry has the extra assumption that
 $\operatorname {gtp}(a/M_0)$
does not
$\operatorname {gtp}(a/M_0)$
does not
 $\mu $
-fork over
$\mu $
-fork over
 $M_0$
, but this is always true by Proposition 4.12.
$M_0$
, but this is always true by Proposition 4.12.
6 Symmetry and saturated models
As mentioned in the previous section, [Reference VanDieren and Vasey31, Corollary 1.4] deduced symmetry from superstability and obtained the uniqueness of limit models. It is natural to localize such argument, which was partially done in the following.
Fact 6.1 [Reference Boney and VanDieren10, Theorem 20].
Assume
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $(\mu ,\chi )$
-symmetry (together with Assumption 2.1). Then it has the uniqueness of
$(\mu ,\chi )$
-symmetry (together with Assumption 2.1). Then it has the uniqueness of
![]() $(\mu ,\geq \chi )$
-limit models: let
$(\mu ,\geq \chi )$
-limit models: let
![]() $M_0,M_1,M_2\in K_{\mu }$
. If both
$M_0,M_1,M_2\in K_{\mu }$
. If both
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are
$M_2$
are
![]() $(\mu ,\geq \chi )$
-limit over
$(\mu ,\geq \chi )$
-limit over
![]() $M_0$
, then
$M_0$
, then
![]() $M_1\cong _{M_0}M_2$
.
$M_1\cong _{M_0}M_2$
.
In the original proof of the above fact, they did not assume tameness. However, we will need tameness when we remove the symmetry assumption (see also the discussion before Lemma 5.7).
Corollary 6.2. There is
![]() $\lambda <h(\mu )$
such that if
$\lambda <h(\mu )$
such that if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda )$
, then:
$[\mu ,\lambda )$
, then:
-
1.
 $\mathbf {K}$
has the uniqueness of
$\mathbf {K}$
has the uniqueness of
 $(\mu ,\geq \chi )$
-limit models.
$(\mu ,\geq \chi )$
-limit models. -
2. If also
 $\mu>\operatorname {LS}(\mathbf {K})$
, any
$\mu>\operatorname {LS}(\mathbf {K})$
, any
 $(\mu ,\geq \chi )$
-limit model is saturated.
$(\mu ,\geq \chi )$
-limit model is saturated.
Proof
-
1. By Corollary 5.13(1),
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $(\mu ,\chi )$
-symmetry. Apply Fact 6.1.
$(\mu ,\chi )$
-symmetry. Apply Fact 6.1. -
2. Suppose
 $\mu $
is regular. Since
$\mu $
is regular. Since
 $\chi \leq \mu $
, any
$\chi \leq \mu $
, any
 $(\mu ,\geq \chi )$
-limit is isomorphic to a
$(\mu ,\geq \chi )$
-limit is isomorphic to a
 $(\mu ,\mu )$
-limit, which is saturated. Suppose
$(\mu ,\mu )$
-limit, which is saturated. Suppose
 $\mu $
is singular. Let M be a
$\mu $
is singular. Let M be a
 $(\mu ,\geq \chi )$
-limit model. We show that it is
$(\mu ,\geq \chi )$
-limit model. We show that it is
 $\delta $
-saturated for any regular
$\delta $
-saturated for any regular
 $\delta <\mu $
. Since
$\delta <\mu $
. Since
 $\delta +\chi $
is a regular cardinal in
$\delta +\chi $
is a regular cardinal in
 $[\chi ,\mu ^+)$
, M is also
$[\chi ,\mu ^+)$
, M is also
 $(\mu , \delta +\chi )$
-limit, which implies it is
$(\mu , \delta +\chi )$
-limit, which implies it is
 $(\delta +\chi )$
-saturated.
$(\delta +\chi )$
-saturated.
Before stating a remark, we quote a fact in order to compare Vasey’s results with ours (but we will not use that fact in our paper). Continuity of
![]() $\mu $
-nonsplitting in Assumption 2.1 is not needed.
$\mu $
-nonsplitting in Assumption 2.1 is not needed.
Fact 6.3 [Reference Boney and Vasey11, Theorem 5.15].
Let
![]() $\chi _0\geq 2^\mu $
be such that
$\chi _0\geq 2^\mu $
be such that
![]() $\mathbf {K}$
does not have the
$\mathbf {K}$
does not have the
![]() $\mu $
-order property of length
$\mu $
-order property of length
![]() $\chi _0^+$
, define
$\chi _0^+$
, define
![]() $\chi _1:=(2^{2^{\chi _0}})^{+3}$
, and let
$\chi _1:=(2^{2^{\chi _0}})^{+3}$
, and let
![]() $\xi \geq \chi _1$
. If
$\xi \geq \chi _1$
. If
![]() $\mathbf {K}$
is stable in unboundedly many cardinals
$\mathbf {K}$
is stable in unboundedly many cardinals
![]() $<\xi $
, then any increasing chain of
$<\xi $
, then any increasing chain of
![]() $\xi $
-saturated models of length
$\xi $
-saturated models of length
![]() $\geq \chi $
is
$\geq \chi $
is
![]() $\xi $
-saturated.
$\xi $
-saturated.
Remark 6.4. We assumed enough stability to get a local result: the same
![]() $\mu $
was considered throughout. In contrast, [Reference Vasey38, Theorems 6.3 and 11.7] are eventual: Fact 6.3 was heavily used. Some of the hypotheses there require unboundedly many (
$\mu $
was considered throughout. In contrast, [Reference Vasey38, Theorems 6.3 and 11.7] are eventual: Fact 6.3 was heavily used. Some of the hypotheses there require unboundedly many (
![]() $H_1$
-closed) stability cardinals.
$H_1$
-closed) stability cardinals.
Now we turn to an AEC version of Harnik’s Theorem. [Reference Vasey38, Lemma 11.9] improved [Reference VanDieren30, Theorem 1] and showed that the following.
Fact 6.5. Let
![]() $\mathbf {K}$
be
$\mathbf {K}$
be
![]() $\mu $
-tame with a monster model. Let
$\mu $
-tame with a monster model. Let
![]() $\xi \geq \mu ^+$
. Suppose:
$\xi \geq \mu ^+$
. Suppose:
-
1.
 $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
 $\mu $
and
$\mu $
and
 $\xi $
;
$\xi $
; -
2.
 $\langle M_i:i<\delta \rangle $
is an increasing chain of
$\langle M_i:i<\delta \rangle $
is an increasing chain of
 $\xi $
-saturated models;
$\xi $
-saturated models; -
3.
 $\operatorname {cf}(\delta )\geq \chi $
;
$\operatorname {cf}(\delta )\geq \chi $
; -
4.
 $(\xi ,\delta )$
-limit models are saturated,
$(\xi ,\delta )$
-limit models are saturated,
then
![]() $\bigcup _{i<\delta }M_i$
is
$\bigcup _{i<\delta }M_i$
is
![]() $\xi $
-saturated.
$\xi $
-saturated.
We remove the assumption of (4) by assuming more stability and continuity of nonsplitting. Our proof is based on [Reference Vasey38, Lemma 11.9] which have some omissions. For comparison, we write down all the assumptions.
Proposition 6.6. Let
![]() $\mathbf {K}$
be
$\mathbf {K}$
be
![]() $\mu $
-tame with a monster model. Let
$\mu $
-tame with a monster model. Let
![]() $\xi \geq \mu ^+$
. There is
$\xi \geq \mu ^+$
. There is
![]() $\lambda <h(\xi )$
such that if:
$\lambda <h(\xi )$
such that if:
-
1.
 $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
 $\mu $
and
$\mu $
and
 $[\xi ,\lambda )$
,
$[\xi ,\lambda )$
, -
2.
 $\langle M_i:i<\delta \rangle $
is an increasing chain of
$\langle M_i:i<\delta \rangle $
is an increasing chain of
 $\xi $
-saturated models;
$\xi $
-saturated models; -
3.
 $\operatorname {cf}(\delta )\geq \chi $
;
$\operatorname {cf}(\delta )\geq \chi $
; -
4. continuity of
 $\mu $
-nonsplitting and of
$\mu $
-nonsplitting and of
 $\xi $
-nonsplitting holds,
$\xi $
-nonsplitting holds,
then
![]() $\bigcup _{i<\delta }M_i$
is
$\bigcup _{i<\delta }M_i$
is
![]() $\xi $
-saturated.
$\xi $
-saturated.
Before proving the proposition, we need to justify that the local character
![]() $\chi $
(Definition 3.10), which was defined for
$\chi $
(Definition 3.10), which was defined for
![]() $K_{\mu }$
, also applies to
$K_{\mu }$
, also applies to
![]() $K_\xi $
. In other words, we need to show that
$K_\xi $
. In other words, we need to show that
![]() $K_\xi $
has local character of nonsplitting (at most)
$K_\xi $
has local character of nonsplitting (at most)
![]() $\chi $
. (Vasey usually cited this fact as [Reference Vasey33, Section 4], by which he should mean an adaptation of [Reference Vasey33, Lemma 4.11].)
$\chi $
. (Vasey usually cited this fact as [Reference Vasey33, Section 4], by which he should mean an adaptation of [Reference Vasey33, Lemma 4.11].)
Lemma 6.7 (Local character transfer).
If
![]() $\mathbf {K}$
is stable in some
$\mathbf {K}$
is stable in some
![]() $\xi \geq \mu $
, then it has
$\xi \geq \mu $
, then it has
![]() $\chi $
-local character of
$\chi $
-local character of
![]() $\xi $
-nonsplitting.
$\xi $
-nonsplitting.
Proof Let
![]() $\langle M_i:i\leq \delta \rangle $
be u-increasing and continuous in
$\langle M_i:i\leq \delta \rangle $
be u-increasing and continuous in
![]() $K_\xi $
,
$K_\xi $
,
![]() $p\in \operatorname {gS}(M_\delta )$
. By Proposition 4.9, there is
$p\in \operatorname {gS}(M_\delta )$
. By Proposition 4.9, there is
![]() $i<\delta $
such that p does not
$i<\delta $
such that p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_{i}$
. By definition of nonforking, there is
$M_{i}$
. By definition of nonforking, there is
![]() $N<_uM_i$
of size
$N<_uM_i$
of size
![]() $\mu $
such that p does not
$\mu $
such that p does not
![]() $\mu $
-split over N. Suppose
$\mu $
-split over N. Suppose
![]() $p \ \xi $
-splits over
$p \ \xi $
-splits over
![]() $M_{i}$
then it also
$M_{i}$
then it also
![]() $\xi $
-splits over N. By
$\xi $
-splits over N. By
![]() $\mu $
-tameness, it
$\mu $
-tameness, it
![]() $\mu $
-splits over N, contradiction.
$\mu $
-splits over N, contradiction.
Proof of Proposition 6.6
Let
![]() $\delta \geq \chi $
be regular. If
$\delta \geq \chi $
be regular. If
![]() $\delta \geq \xi $
we can use a cofinality argument. So we assume
$\delta \geq \xi $
we can use a cofinality argument. So we assume
![]() $\delta <\xi $
. Let
$\delta <\xi $
. Let
![]() $M_\delta :=\bigcup _{i<\delta }M_i$
and
$M_\delta :=\bigcup _{i<\delta }M_i$
and
![]() $N\in K_\xi $
,
$N\in K_\xi $
,
![]() $N\leq M_\delta $
. Without loss of generality, we may assume for
$N\leq M_\delta $
. Without loss of generality, we may assume for
![]() $i\leq \delta $
,
$i\leq \delta $
,
![]() $M_i\in K_\xi $
: Given a saturated
$M_i\in K_\xi $
: Given a saturated
![]() $M^*\in K_{\geq \xi ^+}$
and some
$M^*\in K_{\geq \xi ^+}$
and some
![]() $N\leq M^*$
of size
$N\leq M^*$
of size
![]() $\leq \xi $
, we can close N into a
$\leq \xi $
, we can close N into a
![]() $(\xi ,\chi )$
-limit
$(\xi ,\chi )$
-limit
![]() $N^*$
. By
$N^*$
. By
![]() $\xi $
-model-homogeneity of
$\xi $
-model-homogeneity of
![]() $M^*$
, we may assume
$M^*$
, we may assume
![]() $N^*\leq M^*$
. By Lemma 6.7 and Corollary 6.2(2), any
$N^*\leq M^*$
. By Lemma 6.7 and Corollary 6.2(2), any
![]() $(\xi ,\geq \chi )$
-limits are saturated, so
$(\xi ,\geq \chi )$
-limits are saturated, so
![]() $N^*$
is saturated. Therefore we can recursively shrink each
$N^*$
is saturated. Therefore we can recursively shrink each
![]() $M_i$
to a saturated model in
$M_i$
to a saturated model in
![]() $K_\xi $
while still containing the same intersection with N.
$K_\xi $
while still containing the same intersection with N.
Extend p to a type in
![]() $\operatorname {gS}(M_\delta )$
. By Fact 4.10, there is
$\operatorname {gS}(M_\delta )$
. By Fact 4.10, there is
![]() $i<\delta $
such that p does not
$i<\delta $
such that p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $M_i$
. By reindexing assume
$M_i$
. By reindexing assume
![]() $i=0$
and let
$i=0$
and let
![]() $M_0^0\in K_{\mu }$
witness the nonforking. Obtain
$M_0^0\in K_{\mu }$
witness the nonforking. Obtain
![]() $N_0\in K_{\mu }$
such that
$N_0\in K_{\mu }$
such that
![]() $M_0^0<_uN_0\leq M_0$
in
$M_0^0<_uN_0\leq M_0$
in
![]() $K_{\mu }$
. Define
$K_{\mu }$
. Define
![]() $\mu ':=\mu +\delta $
, we build
$\mu ':=\mu +\delta $
, we build
![]() $\langle N_i:1\leq i\leq \delta \rangle $
increasing and continuous in
$\langle N_i:1\leq i\leq \delta \rangle $
increasing and continuous in
![]() $K_{\mu '}$
such that
$K_{\mu '}$
such that
![]() $N_0\leq N_1\leq N\leq N_\delta $
and for
$N_0\leq N_1\leq N\leq N_\delta $
and for
![]() $i\leq \delta $
,
$i\leq \delta $
,
![]() $N_i\leq M_i$
. Now we construct:
$N_i\leq M_i$
. Now we construct:
-
1.
 $\langle M_i^*,f_{i,j}:i\leq j<\delta \rangle $
an increasing and continuous directed system.
$\langle M_i^*,f_{i,j}:i\leq j<\delta \rangle $
an increasing and continuous directed system. -
2. For
 $i<\delta $
,
$i<\delta $
,
 $M_i^*\in K_\xi $
,
$M_i^*\in K_\xi $
,
 $N_i\leq M_i^*\leq M_i$
.
$N_i\leq M_i^*\leq M_i$
. -
3. For
 $i<\delta $
,
$i<\delta $
,
 $f_{i,i+1}:M_i^*\xrightarrow [N_i]{}M_{i+1}^*$
.
$f_{i,i+1}:M_i^*\xrightarrow [N_i]{}M_{i+1}^*$
. -
4.
 $M_0^*:= M_0$
. For
$M_0^*:= M_0$
. For
 $i<\delta $
,
$i<\delta $
,
 $M_i^*<_uM_{i+1}^*$
.
$M_i^*<_uM_{i+1}^*$
.

At limit stage
![]() $i<\delta $
, take direct limit
$i<\delta $
, take direct limit
![]() $M_i^*$
which contains
$M_i^*$
which contains
![]() $N_i$
. Since
$N_i$
. Since
![]() $\Vert N_i \Vert <\xi $
and
$\Vert N_i \Vert <\xi $
and
![]() $M_i$
is model-homogeneous, we may assume
$M_i$
is model-homogeneous, we may assume
![]() $M_i^*$
is inside
$M_i^*$
is inside
![]() $M_i$
. Suppose
$M_i$
. Suppose
![]() $M_i^*$
is constructed for some
$M_i^*$
is constructed for some
![]() $i<\delta $
, obtain the amalgam
$i<\delta $
, obtain the amalgam
![]() $M_{i+1}^{**}$
of
$M_{i+1}^{**}$
of
![]() $M_i^*$
and
$M_i^*$
and
![]() $N_{i+1}$
over
$N_{i+1}$
over
![]() $N_i$
. Since
$N_i$
. Since
![]() $\Vert N_{i+1} \Vert <\xi $
and
$\Vert N_{i+1} \Vert <\xi $
and
![]() $M_{i+1}$
is model-homogeneous, we may embed the amalgam into
$M_{i+1}$
is model-homogeneous, we may embed the amalgam into
![]() $M_{i+1}$
. Call the image of the amalgam
$M_{i+1}$
. Call the image of the amalgam
![]() $M_{i+1}^*$
. After the construction, take one more direct limit to obtain
$M_{i+1}^*$
. After the construction, take one more direct limit to obtain
![]() $(M_\delta ^*,f_{i,\delta })_{i<\delta }$
(but this time we do not know if
$(M_\delta ^*,f_{i,\delta })_{i<\delta }$
(but this time we do not know if
![]() $M_\delta ^*\leq M_\delta $
). By item (4) above, we have that
$M_\delta ^*\leq M_\delta $
). By item (4) above, we have that
![]() $M_\delta ^*$
is a
$M_\delta ^*$
is a
![]() $(\xi ,\delta )$
-limit, hence saturated.
$(\xi ,\delta )$
-limit, hence saturated.
We will work in a local monster model, namely we find a saturated
![]() $\tilde {M}\in K_\xi $
such that:
$\tilde {M}\in K_\xi $
such that:
-
a.
 $\tilde {M}$
contains
$\tilde {M}$
contains
 $M_\delta $
and
$M_\delta $
and
 $M_\delta ^*$
.
$M_\delta ^*$
. -
b. For
 $i<\delta $
,
$i<\delta $
,
 $f_{i,\delta }$
can be extended to
$f_{i,\delta }$
can be extended to
 $f_{i,\delta }^*\in \operatorname {Aut}(\tilde {M})$
.
$f_{i,\delta }^*\in \operatorname {Aut}(\tilde {M})$
. -
c. For
 $i<\delta $
,
$i<\delta $
,
 $f_{i,\delta }^*[N_\delta ]\leq M_\delta ^*$
.
$f_{i,\delta }^*[N_\delta ]\leq M_\delta ^*$
.
(c) is possible because
![]() $M_\delta ^*$
is universal over
$M_\delta ^*$
is universal over
![]() $f_{i,\delta }[M_i^*]$
. Finally, we define
$f_{i,\delta }[M_i^*]$
. Finally, we define
![]() $N^*\leq M_\delta ^*$
of size
$N^*\leq M_\delta ^*$
of size
![]() $\mu '$
containing
$\mu '$
containing
![]() $\bigcup _{i<\delta }f_{i,\delta }^*[N_\delta ]$
. By model-homogeneity of
$\bigcup _{i<\delta }f_{i,\delta }^*[N_\delta ]$
. By model-homogeneity of
![]() $M_\delta ^*$
, we build
$M_\delta ^*$
, we build
![]() $M^{**}\in K_\xi $
saturated such that
$M^{**}\in K_\xi $
saturated such that
![]() $N^*\leq M^{**}<_uM_\delta ^*$
.
$N^*\leq M^{**}<_uM_\delta ^*$
.
By Proposition 4.2, extend p to
![]() $q\in \operatorname {gS}(\tilde {M})$
nonforking over
$q\in \operatorname {gS}(\tilde {M})$
nonforking over
![]() $N_0$
(here we need
$N_0$
(here we need
![]() $N_0\in K_{\mu }$
or else we have to assume more stability). Since
$N_0\in K_{\mu }$
or else we have to assume more stability). Since
![]() $M_\delta ^*>_uM^{**}$
, we can find
$M_\delta ^*>_uM^{**}$
, we can find
![]() $b_\delta \in M_\delta ^*$
such that
$b_\delta \in M_\delta ^*$
such that
![]() $b_\delta \vDash q\restriction M^{**}$
. Since
$b_\delta \vDash q\restriction M^{**}$
. Since
![]() $M_\delta ^*$
is a direct limit of the
$M_\delta ^*$
is a direct limit of the
![]() $M_i^*$
’s, there is
$M_i^*$
’s, there is
![]() $i<\delta $
such that
$i<\delta $
such that
![]() $f_{i,\delta }(b)=b_\delta $
. As
$f_{i,\delta }(b)=b_\delta $
. As
![]() $b\in M_i^*\subseteq M_i\leq M_\delta $
, it suffices to show that
$b\in M_i^*\subseteq M_i\leq M_\delta $
, it suffices to show that
![]() $b\vDash q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]$
, because
$b\vDash q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]$
, because
![]() $N\leq N_\delta \leq (f_{i,\delta }^*)^{-1}[N^*]\leq (f_{i,\delta }^*)^{-1}[M^{**}]$
. In the following diagram, dotted arrows refer to
$N\leq N_\delta \leq (f_{i,\delta }^*)^{-1}[N^*]\leq (f_{i,\delta }^*)^{-1}[M^{**}]$
. In the following diagram, dotted arrows refer to
![]() $\leq $
or
$\leq $
or
![]() $<_u$
between models, while the dashed equal sign is our goal.
$<_u$
between models, while the dashed equal sign is our goal.

Since
![]() $q\restriction M^{**}=\operatorname {gtp}(b_\delta /M^{**})$
does not
$q\restriction M^{**}=\operatorname {gtp}(b_\delta /M^{**})$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $N_0$
and
$N_0$
and
![]() $f_{i,\delta }^*$
fixes
$f_{i,\delta }^*$
fixes
![]() $N_i\geq N_0$
, by invariance
$N_i\geq N_0$
, by invariance
![]() $\operatorname {gtp}(b/(f_{i,\delta }^*)^{-1}[M^{**}])$
does not
$\operatorname {gtp}(b/(f_{i,\delta }^*)^{-1}[M^{**}])$
does not
![]() $\mu $
-fork
$\mu $
-fork
![]() $N_0$
. By monotonicity, q and hence
$N_0$
. By monotonicity, q and hence
![]() $q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]$
does not
$q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]$
does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $N_0$
. By invariance again,
$N_0$
. By invariance again,
![]() $\operatorname {gtp}(b/N_0)=\operatorname {gtp}(b_\delta /N_0)=q\restriction N_0$
. By Corollary 4.6,
$\operatorname {gtp}(b/N_0)=\operatorname {gtp}(b_\delta /N_0)=q\restriction N_0$
. By Corollary 4.6,
![]() $q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]=\operatorname {gtp}(b/(f_{i,\delta }^*)^{-1}[M^{**}])$
as desired.
$q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]=\operatorname {gtp}(b/(f_{i,\delta }^*)^{-1}[M^{**}])$
as desired.
Remark 6.8.
-
1. In Proposition 6.6, the assumption of stability in
 $[\xi ,\lambda )$
is to guarantee local symmetry from no
$[\xi ,\lambda )$
is to guarantee local symmetry from no
 $\xi $
-order property of length
$\xi $
-order property of length
 $\lambda $
. We can relax the stability assumption if we have the stronger assumption of no
$\lambda $
. We can relax the stability assumption if we have the stronger assumption of no
 $\xi $
-order property. Namely, if
$\xi $
-order property. Namely, if
 $\mathbf {K}$
does not have
$\mathbf {K}$
does not have
 $\xi $
-order property of length
$\xi $
-order property of length
 $\zeta $
where
$\zeta $
where
 $\zeta>\xi $
, then we can simply assume stability in
$\zeta>\xi $
, then we can simply assume stability in
 $[\xi ,\zeta )$
.
$[\xi ,\zeta )$
. -
2. We compare our approach with Vasey’s. To satisfy hypothesis (4) in Fact 6.5, he used Fact 6.1 which requires
 $(\xi ,\chi )$
-symmetry and continuity of nonsplitting [Reference Vasey38, Theorem 11.11(1)]. Meanwhile he obtained the equivalence of
$(\xi ,\chi )$
-symmetry and continuity of nonsplitting [Reference Vasey38, Theorem 11.11(1)]. Meanwhile he obtained the equivalence of
 $(\xi ,\chi )$
-symmetry
$(\xi ,\chi )$
-symmetry
 $\Leftrightarrow $
the increasing union of saturated models of length
$\Leftrightarrow $
the increasing union of saturated models of length
 $\geq \chi $
in
$\geq \chi $
in
 $K_{\xi ^+}$
is saturated (see Fact 6.15). By Fact 6.3, the latter is true for large enough
$K_{\xi ^+}$
is saturated (see Fact 6.15). By Fact 6.3, the latter is true for large enough
 $\xi $
. In short, he raised the cardinal threshold while we assumed more stability. More curiously, both our stability assumption and his cardinal threshold are linked to no order property.
$\xi $
. In short, he raised the cardinal threshold while we assumed more stability. More curiously, both our stability assumption and his cardinal threshold are linked to no order property.A comparison table can be found below. For
 $\xi \geq \mu $
, we abbreviate the increasing union of saturated models of length
$\xi \geq \mu $
, we abbreviate the increasing union of saturated models of length
 $\geq \chi $
in
$\geq \chi $
in
 $K_{\xi }$
is saturated by “Union(
$K_{\xi }$
is saturated by “Union(
 $\xi $
).”
$\xi $
).”

Observation 6.9. The
![]() $[\xi ,\lambda )$
stability assumption in Proposition 6.6 can be replaced by
$[\xi ,\lambda )$
stability assumption in Proposition 6.6 can be replaced by
![]() $(\xi ,\chi )$
-symmetry, because we can directly apply Fact 6.1 instead of using extra stability to invoke Corollary 6.2. This applies to other results in the paper.
$(\xi ,\chi )$
-symmetry, because we can directly apply Fact 6.1 instead of using extra stability to invoke Corollary 6.2. This applies to other results in the paper.
We now recover two known results with different proofs. The original proof for [Reference Vasey32, Proposition 10.10] is extremely abstract so we supplement a direct argument. (Here we already assumed a monster model which implies no maximal models everywhere. Alternatively, one can adapt the proof of [Reference Boney4, Theorem 7.1] without using symmetry to transfer no maximal models upward.) On the other hand, since we have generalized the arguments in [Reference VanDieren and Vasey31], we can specialize them to
![]() $\chi ={\aleph _0}$
and recover [Reference VanDieren and Vasey31, Corollary 6.10] (see below). In their approach, [Reference VanDieren30, Theorem 22] was cited for the successor case of
$\chi ={\aleph _0}$
and recover [Reference VanDieren and Vasey31, Corollary 6.10] (see below). In their approach, [Reference VanDieren30, Theorem 22] was cited for the successor case of
![]() $\lambda $
and the limit case was proven by inductive hypothesis. Here we show each case of
$\lambda $
and the limit case was proven by inductive hypothesis. Here we show each case of
![]() $\lambda $
separately in Corollary 6.11(2). They also glossed over the computation of the Löwenheim–Skolem number so we add details.
$\lambda $
separately in Corollary 6.11(2). They also glossed over the computation of the Löwenheim–Skolem number so we add details.
The following facts do not require continuity of nonsplitting.
Fact 6.10.
-
1. [Reference Baldwin, Kueker and VanDieren1, Theorem 1] Let
 $\xi \geq \mu $
. If
$\xi \geq \mu $
. If
 $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
 $\xi $
, then it is also stable in
$\xi $
, then it is also stable in
 $\xi ^{+n}$
for all
$\xi ^{+n}$
for all
 $n<\omega $
.
$n<\omega $
. -
2. [Reference Vasey33, Theorem 5.5] Let
 $\xi \geq \mu $
,
$\xi \geq \mu $
,
 $\delta $
be regular,
$\delta $
be regular,
 $\langle \xi _i:i<\delta \rangle $
be strictly increasing stability cardinals and
$\langle \xi _i:i<\delta \rangle $
be strictly increasing stability cardinals and
 $\xi _0=\xi $
. If
$\xi _0=\xi $
. If
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\delta $
-local character of
$\delta $
-local character of
 $\xi $
-nonsplitting, then
$\xi $
-nonsplitting, then
 $\sup _{i<\delta }\xi _i$
is also a stability cardinal. In particular, if
$\sup _{i<\delta }\xi _i$
is also a stability cardinal. In particular, if
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\xi $
-superstable, then it is stable in all
$\xi $
-superstable, then it is stable in all
 $\lambda \geq \xi $
.
$\lambda \geq \xi $
.
Corollary 6.11.
-
1. [Reference Vasey32, Proposition 10.10] Let
 $\xi \geq \mu $
. If
$\xi \geq \mu $
. If
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\xi $
-superstable, then it is superstable in all
$\xi $
-superstable, then it is superstable in all
 $\zeta \geq \xi $
.
$\zeta \geq \xi $
. -
2. Let
 $\xi \geq \mu ^+$
. If
$\xi \geq \mu ^+$
. If
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\xi $
-superstable, then
$\xi $
-superstable, then
 $\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$
the class of
$\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$
the class of
 $\xi $
-saturated models in
$\xi $
-saturated models in
 $\mathbf {K}$
forms an AEC with Löwenheim–Skolem number
$\mathbf {K}$
forms an AEC with Löwenheim–Skolem number
 $\xi $
.
$\xi $
. -
3. [Reference VanDieren and Vasey31, Corollary 6.10] Let
 $\xi \geq \mu ^+$
. If
$\xi \geq \mu ^+$
. If
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\xi $
-superstable, then for
$\xi $
-superstable, then for
 $\lambda \geq \xi $
,
$\lambda \geq \xi $
,
 $\mathbf {K}^{\boldsymbol {\lambda \text {-}sat}}$
the class of
$\mathbf {K}^{\boldsymbol {\lambda \text {-}sat}}$
the class of
 $\lambda $
-saturated models in
$\lambda $
-saturated models in
 $\mathbf {K}$
forms an AEC with Löwenheim–Skolem number
$\mathbf {K}$
forms an AEC with Löwenheim–Skolem number
 $\lambda $
.
$\lambda $
.
Proof
-
2. By (1) and Proposition 3.16, we have continuity of
 $\xi $
-nonsplitting and stability in
$\xi $
-nonsplitting and stability in
 $[\xi ,\infty )$
. By Proposition 6.6,
$[\xi ,\infty )$
. By Proposition 6.6,
 $\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$
is closed under chains. Given a
$\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$
is closed under chains. Given a
 $\xi $
-saturated model M and
$\xi $
-saturated model M and
 $A\subseteq |M|$
, we need to find
$A\subseteq |M|$
, we need to find
 $N\leq M$
containing A such that
$N\leq M$
containing A such that
 $\Vert N \Vert \leq |A|+\xi $
. We prove this by induction on
$\Vert N \Vert \leq |A|+\xi $
. We prove this by induction on
 $|A|$
. The first paragraph of the proof of Proposition 6.6 shows how to handle the case
$|A|$
. The first paragraph of the proof of Proposition 6.6 shows how to handle the case
 $|{A}|\leq \xi $
. Suppose
$|{A}|\leq \xi $
. Suppose
 $|{A}|>\xi $
, then resolve
$|{A}|>\xi $
, then resolve
 $A=\bigcup _{i<|A|}{A_i}$
where
$A=\bigcup _{i<|A|}{A_i}$
where
 $A_i$
are increasing and of size
$A_i$
are increasing and of size
 $<|A|$
. For each
$<|A|$
. For each
 $i<|A|$
, use the inductive hypothesis and close each
$i<|A|$
, use the inductive hypothesis and close each
 $A_i$
into a
$A_i$
into a
 $\xi $
-saturated
$\xi $
-saturated
 $N_i\leq M$
of size
$N_i\leq M$
of size
 $|A_i|+\xi $
with
$|A_i|+\xi $
with
 $N_i\geq N_j$
for
$N_i\geq N_j$
for
 $j<i$
. As
$j<i$
. As
 $\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$
is closed under chains,
$\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$
is closed under chains,
 $\bigcup _{i<|A|}N_i$
is
$\bigcup _{i<|A|}N_i$
is
 $\xi $
-saturated, of size
$\xi $
-saturated, of size
 $|A|$
and contains A.
$|A|$
and contains A. -
3. Combine (1) and (2).
It is natural to ask if there are converses to our results. In particular what are the sufficient conditions to
![]() $\mathbf {K}$
having the
$\mathbf {K}$
having the
![]() $\chi $
-local character in
$\chi $
-local character in
![]() $K_\xi $
for some
$K_\xi $
for some
![]() $\xi \geq \mu $
. Vasey [Reference Vasey38, Lemma 4.12] gave one useful criterion which we adapt below. The original statement did not cover the case
$\xi \geq \mu $
. Vasey [Reference Vasey38, Lemma 4.12] gave one useful criterion which we adapt below. The original statement did not cover the case
![]() $\delta =\xi $
below and such omission affects the rest of his results. In particular [Reference Vasey38, Theorem 4.11] should only apply to singular
$\delta =\xi $
below and such omission affects the rest of his results. In particular [Reference Vasey38, Theorem 4.11] should only apply to singular
![]() $\mu $
there. Our result covers regular cardinals because we assume stability and continuity of nonsplitting. Only in [Reference Vasey38, Section 11] did he start to assume continuity of nonsplitting and in [Reference Vasey38, Theorem 12.1] did he take care of the regular case by under extra assumptions.
$\mu $
there. Our result covers regular cardinals because we assume stability and continuity of nonsplitting. Only in [Reference Vasey38, Section 11] did he start to assume continuity of nonsplitting and in [Reference Vasey38, Theorem 12.1] did he take care of the regular case by under extra assumptions.
We state the full assumptions in the following proposition.
Proposition 6.12. Let
![]() $\mu \geq \operatorname {LS}(\mathbf {K})$
. Suppose
$\mu \geq \operatorname {LS}(\mathbf {K})$
. Suppose
![]() $\mathbf {K}$
has a monster model, is
$\mathbf {K}$
has a monster model, is
![]() $\mu $
-tame and stable in some
$\mu $
-tame and stable in some
![]() $\xi \geq \mu ^+$
. Let
$\xi \geq \mu ^+$
. Let
![]() $\delta <\xi ^+$
be regular,
$\delta <\xi ^+$
be regular,
![]() $\langle M_i:i\leq \delta \rangle $
be u-increasing and continuous in
$\langle M_i:i\leq \delta \rangle $
be u-increasing and continuous in
![]() $K_\xi $
,
$K_\xi $
,
![]() $M_\delta $
is
$M_\delta $
is
![]() $(\mu +\delta )^+$
-saturated and
$(\mu +\delta )^+$
-saturated and
![]() $p\in \operatorname {gS}(M_\delta )$
. There is
$p\in \operatorname {gS}(M_\delta )$
. There is
![]() $i<\delta $
such that p does not
$i<\delta $
such that p does not
![]() $\xi $
-split over
$\xi $
-split over
![]() $M_i$
if one of the following holds:
$M_i$
if one of the following holds:
-
1.
 $\delta =\xi $
(so
$\delta =\xi $
(so
 $\xi $
is regular),
$\xi $
is regular),
 $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
 $\xi $
-nonsplitting.
$\xi $
-nonsplitting. -
2.
 $\delta =\xi $
,
$\delta =\xi $
,
 $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
 $\mu $
and has continuity of
$\mu $
and has continuity of
 $\mu $
-nonsplitting.
$\mu $
-nonsplitting. -
3.
 $\delta <\xi $
.
$\delta <\xi $
.
Proof The first case is by Proposition 3.9 (with
![]() $\xi $
in place of
$\xi $
in place of
![]() $\mu $
). The second case is by Lemma 6.7. We consider the case
$\mu $
). The second case is by Lemma 6.7. We consider the case
![]() $\delta <\xi $
. Suppose the conclusion is false, then for
$\delta <\xi $
. Suppose the conclusion is false, then for
![]() $i<\delta $
, there exist:
$i<\delta $
, there exist:
-
1.
 $N_i^0,N_i^1,N_i^2\in K_\xi $
with
$N_i^0,N_i^1,N_i^2\in K_\xi $
with
 $N_i^0\leq N_i^1,N_i^2\leq M_\delta $
.
$N_i^0\leq N_i^1,N_i^2\leq M_\delta $
. -
2.
 $f_i:N_i^1\xrightarrow [N_i^0]{}N_i^2$
with
$f_i:N_i^1\xrightarrow [N_i^0]{}N_i^2$
with
 $f_i(p\restriction N_i^1)\neq p\restriction N_i^2$
.
$f_i(p\restriction N_i^1)\neq p\restriction N_i^2$
. -
3.
 $M_i^1\leq N_i^1$
and
$M_i^1\leq N_i^1$
and
 $M_i^2\leq N_i^2$
such that
$M_i^2\leq N_i^2$
such that
 $f_i[M_i^1]\cong M_i^2$
and
$f_i[M_i^1]\cong M_i^2$
and
 $f_i(p\restriction M_i^1)\neq p\restriction M_i^2$
.
$f_i(p\restriction M_i^1)\neq p\restriction M_i^2$
.
Let
![]() $N\leq M$
of size
$N\leq M$
of size
![]() $\mu +\delta $
containing
$\mu +\delta $
containing
![]() $M_i^1$
and
$M_i^1$
and
![]() $M_i^2$
for all
$M_i^2$
for all
![]() $i<\delta $
. Since
$i<\delta $
. Since
![]() $M_\delta $
is
$M_\delta $
is
![]() $(\mu +\delta )^+$
-saturated, there is
$(\mu +\delta )^+$
-saturated, there is
![]() $b\in |M_\delta |$
realizing
$b\in |M_\delta |$
realizing
![]() $p\restriction N$
. Then there is
$p\restriction N$
. Then there is
![]() $i<\delta $
such that
$i<\delta $
such that
![]() $b\in |M_i|$
. Since
$b\in |M_i|$
. Since
![]() $f_i$
fixes
$f_i$
fixes
![]() $M_i$
, it also fixes b. Thus
$M_i$
, it also fixes b. Thus
contradicting item (3) above.
Corollary 6.13. Suppose
![]() $\xi \geq \mu ^+$
and
$\xi \geq \mu ^+$
and
![]() $\delta <\xi ^+$
be regular. If
$\delta <\xi ^+$
be regular. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $\xi $
, has continuity of
$\xi $
, has continuity of
![]() $\xi $
-nonsplitting and has unique
$\xi $
-nonsplitting and has unique
![]() $(\xi ,\geq \delta )$
-limit models, then it has
$(\xi ,\geq \delta )$
-limit models, then it has
![]() $\delta $
-local character in
$\delta $
-local character in
![]() $K_\xi $
. If in addition
$K_\xi $
. If in addition
![]() $K_\xi $
has unique limit models, then it is
$K_\xi $
has unique limit models, then it is
![]() $\xi $
-superstable.
$\xi $
-superstable.
Proof Let
![]() $\delta '\geq \delta $
be regular and
$\delta '\geq \delta $
be regular and
![]() $\langle M_i:i\leq \delta '\rangle $
be u-increasing and continuous,
$\langle M_i:i\leq \delta '\rangle $
be u-increasing and continuous,
![]() $p\in \operatorname {gS}(M_{\delta '})$
. By the proof of Corollary 6.2(2),
$p\in \operatorname {gS}(M_{\delta '})$
. By the proof of Corollary 6.2(2),
![]() $M_{\delta '}$
is saturated. By Proposition 6.12, there is
$M_{\delta '}$
is saturated. By Proposition 6.12, there is
![]() $i<\delta '$
such that p does not
$i<\delta '$
such that p does not
![]() $\xi $
-split over
$\xi $
-split over
![]() $M_i$
.
$M_i$
.
Remark 6.14. As before, our result is local. Grossberg and Vasey [Reference Grossberg and Vasey18, Theorem 3.18] proved a similar result which is eventual: they managed to guarantee superstability after
![]() $\beth _\omega (\chi _0)$
where
$\beth _\omega (\chi _0)$
where
![]() $\mathbf {K}$
has no order property of length
$\mathbf {K}$
has no order property of length
![]() $\chi _0$
.
$\chi _0$
.
Vasey [Reference Vasey38, Fact 11.6] also made another observation that connects saturated models and symmetry. In the original statement, he omitted writing continuity of nonsplitting in the hypothesis and did not give a proof sketch, so we give more details here (Assumption 2.1 applies). As in the discussion before Definition 5.1, we consider the tail of regular cardinals
![]() $\delta '\geq \delta $
in place of a fixed
$\delta '\geq \delta $
in place of a fixed
![]() $\delta '=\delta $
to match our notations.
$\delta '=\delta $
to match our notations.
Fact 6.15. Let
![]() $\delta <\mu ^+$
be regular. If for any
$\delta <\mu ^+$
be regular. If for any
![]() $\delta '\in [\delta ,\mu ^+)$
regular, any
$\delta '\in [\delta ,\mu ^+)$
regular, any
![]() $\langle M_i:i<\delta '\rangle $
increasing chain of saturated models in
$\langle M_i:i<\delta '\rangle $
increasing chain of saturated models in
![]() $K_{\mu ^+}$
has a saturated union, then
$K_{\mu ^+}$
has a saturated union, then
![]() $ \mathbf {K}$
has
$ \mathbf {K}$
has
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
Proof In [Reference VanDieren29, Theorem 2], it was shown that if the above fact holds for any
![]() $\delta <\mu ^+$
, then any reduced tower is continuous at all
$\delta <\mu ^+$
, then any reduced tower is continuous at all
![]() $\delta <\mu ^+$
. We can localize this argument to show that if the above fact holds for a specific
$\delta <\mu ^+$
. We can localize this argument to show that if the above fact holds for a specific
![]() $\delta <\mu ^+$
, then any reduced tower is continuous at
$\delta <\mu ^+$
, then any reduced tower is continuous at
![]() $\geq \delta $
. By [Reference Boney and VanDieren10, Proposition 19],
$\geq \delta $
. By [Reference Boney and VanDieren10, Proposition 19],
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $(\mu ,\delta )$
-symmetry.
$(\mu ,\delta )$
-symmetry.
Corollary 6.16. Let
![]() $\delta <\mu ^+$
be regular. If for any
$\delta <\mu ^+$
be regular. If for any
![]() $\delta '\in [\delta ,\mu ^+)$
regular, any
$\delta '\in [\delta ,\mu ^+)$
regular, any
![]() $\langle M_i:i<\delta '\rangle $
increasing chain of saturated models in
$\langle M_i:i<\delta '\rangle $
increasing chain of saturated models in
![]() $K_{\mu ^+}$
has a saturated union, then
$K_{\mu ^+}$
has a saturated union, then
![]() $ \mathbf {K}$
has uniqueness of
$ \mathbf {K}$
has uniqueness of
![]() $(\mu ,\geq \delta )$
-limit models.
$(\mu ,\geq \delta )$
-limit models.
Question 6.17. Is there an analog of Fact 6.15 and Corollary 6.16 where “
![]() $\mu ^+$
” is replaced by a general
$\mu ^+$
” is replaced by a general
![]() $\xi \geq \mu ^+$
?
$\xi \geq \mu ^+$
?
We look at superlimits and solvability before ending this section. The following localizes [Reference Shelah and Vasey25, Definition 2.1], which is more natural than [Reference Vasey38, Definition 6.2].
Definition 6.18. Let
![]() $\xi \geq \mu $
.
$\xi \geq \mu $
.
![]() $M\in K_\xi $
is a
$M\in K_\xi $
is a
![]() $\chi $
-superlimit if M is universal in
$\chi $
-superlimit if M is universal in
![]() $K_\xi $
, not maximal, and for any regular
$K_\xi $
, not maximal, and for any regular
![]() $\delta $
with
$\delta $
with
![]() $\chi \leq \delta <\xi ^+$
,
$\chi \leq \delta <\xi ^+$
,
![]() $\langle M_i:i<\delta \rangle $
increasing such that
$\langle M_i:i<\delta \rangle $
increasing such that
![]() $M_i\cong M$
for all
$M_i\cong M$
for all
![]() $i<\delta $
, then
$i<\delta $
, then
![]() $\bigcup _{i<\delta }M_i\cong M$
. M is called a superlimit if it is a
$\bigcup _{i<\delta }M_i\cong M$
. M is called a superlimit if it is a
![]() ${\aleph _0}$
-superlimit.
${\aleph _0}$
-superlimit.
Proposition 6.19. Let
![]() $\mathbf {K}$
have continuity of
$\mathbf {K}$
have continuity of
![]() $\xi $
-nonsplitting for some
$\xi $
-nonsplitting for some
![]() $\xi \geq \mu ^+$
. There is
$\xi \geq \mu ^+$
. There is
![]() $\lambda <h(\xi )$
such that if
$\lambda <h(\xi )$
such that if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\xi ,\lambda )$
, then it has a saturated
$[\xi ,\lambda )$
, then it has a saturated
![]() $\chi $
-superlimit in
$\chi $
-superlimit in
![]() $K_\xi $
.
$K_\xi $
.
Proof By Corollary 6.2(2) and Lemma 6.7, any
![]() $(\xi ,\geq \chi )$
-limit M is saturated (hence universal in
$(\xi ,\geq \chi )$
-limit M is saturated (hence universal in
![]() $K_\xi $
). Let
$K_\xi $
). Let
![]() $\delta $
be regular,
$\delta $
be regular,
![]() $\chi \leq \delta <\xi ^+$
,
$\chi \leq \delta <\xi ^+$
,
![]() $\langle M_i:i<\delta \rangle $
increasing such that
$\langle M_i:i<\delta \rangle $
increasing such that
![]() $M_i\cong M$
for all
$M_i\cong M$
for all
![]() $i<\delta $
. Then all
$i<\delta $
. Then all
![]() $M_i$
are saturated in
$M_i$
are saturated in
![]() $K_\xi $
. By Proposition 6.6,
$K_\xi $
. By Proposition 6.6,
![]() $\bigcup _{i<\delta }M_i$
is also saturated, hence isomorphic to M.
$\bigcup _{i<\delta }M_i$
is also saturated, hence isomorphic to M.
Remark 6.20. The specific
![]() $\chi $
-superlimit built above is saturated. Under the same assumptions, it is true for all
$\chi $
-superlimit built above is saturated. Under the same assumptions, it is true for all
![]() $\chi $
-superlimits (Lemma 6.23).
$\chi $
-superlimits (Lemma 6.23).
The following connects superlimit models with solvability (see [Reference Grossberg and Vasey18, Definition 2.17] for a definition).
Fact 6.21 [Reference Grossberg and Vasey18, Lemma 2.19].
Let
![]() $\lambda \geq \xi $
. The following are equivalent:
$\lambda \geq \xi $
. The following are equivalent:
-
1.
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(\lambda ,\xi )$
-solvable.
$(\lambda ,\xi )$
-solvable. -
2. There exists an AEC
 $\mathbf {K'}$
in
$\mathbf {K'}$
in
 ${\operatorname {L}(\mathbf {K'})}\supseteq \operatorname {L}( \mathbf {K})$
such that
${\operatorname {L}(\mathbf {K'})}\supseteq \operatorname {L}( \mathbf {K})$
such that
 $\operatorname {LS}(\mathbf {K'})\leq \xi $
,
$\operatorname {LS}(\mathbf {K'})\leq \xi $
,
 $\mathbf {K'}$
has arbitrarily large models and for any
$\mathbf {K'}$
has arbitrarily large models and for any
 $M\in K^{\prime }_\lambda $
,
$M\in K^{\prime }_\lambda $
,
 $M\restriction \operatorname {L}(\mathbf {K})$
is a superlimit in
$M\restriction \operatorname {L}(\mathbf {K})$
is a superlimit in
 $\mathbf {K}$
.
$\mathbf {K}$
.
In [Reference Grossberg and Vasey18, Theorem 4.9], they showed that
![]() $(\lambda ,\xi )$
-solvability is eventually (in
$(\lambda ,\xi )$
-solvability is eventually (in
![]() $\lambda $
) equivalent to other criteria of superstability (modulo a jump of
$\lambda $
) equivalent to other criteria of superstability (modulo a jump of
![]() $\beth _{\omega +2}$
). Also,
$\beth _{\omega +2}$
). Also,
![]() $\lambda $
is required to be greater than
$\lambda $
is required to be greater than
![]() $\xi $
. We propose that a better formulation of superstability which has
$\xi $
. We propose that a better formulation of superstability which has
![]() $\lambda =\xi $
. The case
$\lambda =\xi $
. The case
![]() $\lambda>\xi $
should be a stronger condition because it allows downward transfer (see [Reference Vasey36, Corollary 5.1] for more development on this). Our result proceeds with a series of lemmas.
$\lambda>\xi $
should be a stronger condition because it allows downward transfer (see [Reference Vasey36, Corollary 5.1] for more development on this). Our result proceeds with a series of lemmas.
The next lemma generalizes [Reference Grossberg and Vasey18, Fact 2.8(5)] (which is based on [Reference Drueck13]).
Lemma 6.22. Let
![]() $\xi \geq \mu ^+$
and let M be a saturated model in
$\xi \geq \mu ^+$
and let M be a saturated model in
![]() $K_\xi $
. M is a
$K_\xi $
. M is a
![]() $\chi $
-superlimit iff for any regular
$\chi $
-superlimit iff for any regular
![]() $\delta $
with
$\delta $
with
![]() $\chi \leq \delta <\xi ^+$
, any increasing chain of saturated models in
$\chi \leq \delta <\xi ^+$
, any increasing chain of saturated models in
![]() $K_\xi $
of length
$K_\xi $
of length
![]() $\delta $
has a saturated union.
$\delta $
has a saturated union.
Proof Immediate from the definition of a
![]() $\chi $
-superlimit. Notice that we need
$\chi $
-superlimit. Notice that we need
![]() $\delta <\xi ^+$
to make sure that the chain of saturated models have a union in
$\delta <\xi ^+$
to make sure that the chain of saturated models have a union in
![]() $K_\xi $
.
$K_\xi $
.
The following lemma generalizes [Reference Drueck13, Theorem 2.3.11].
Lemma 6.23. Let
![]() $\xi>\operatorname {LS}(\mathbf {K})$
. If M is a
$\xi>\operatorname {LS}(\mathbf {K})$
. If M is a
![]() $\chi $
-superlimit in
$\chi $
-superlimit in
![]() $K_\xi $
, then M is saturated.
$K_\xi $
, then M is saturated.
Proof We show that M is a
![]() $(\xi ,\delta )$
-limit for regular
$(\xi ,\delta )$
-limit for regular
![]() $\delta \in [\chi ,\xi ^+)$
. If done, the argument in Corollary 6.2(2) shows that it is saturated. Construct
$\delta \in [\chi ,\xi ^+)$
. If done, the argument in Corollary 6.2(2) shows that it is saturated. Construct
![]() $\langle M_i,N_i:i<\delta \rangle $
in
$\langle M_i,N_i:i<\delta \rangle $
in
![]() $K_\xi $
such that
$K_\xi $
such that
![]() $M_0:= M\cong M_i<_uN_i<M_{i+1}$
for
$M_0:= M\cong M_i<_uN_i<M_{i+1}$
for
![]() $i<\delta $
. Suppose
$i<\delta $
. Suppose
![]() $N_i$
is constructed, by universality
$N_i$
is constructed, by universality
![]() $N_i$
embeds inside M so we can build
$N_i$
embeds inside M so we can build
![]() $M_{i+1}$
, an isomorphic copy of M over
$M_{i+1}$
, an isomorphic copy of M over
![]() $N_i$
. To construct
$N_i$
. To construct
![]() $M_i$
for limit i, we embed the union of previous
$M_i$
for limit i, we embed the union of previous
![]() $N_i$
inside M and repeat the above process. By the property of a
$N_i$
inside M and repeat the above process. By the property of a
![]() $\chi $
-superlimit,
$\chi $
-superlimit,
![]() $M\cong \bigcup _{i<\delta }M_i=\bigcup _{i<\delta }N_i$
which is a
$M\cong \bigcup _{i<\delta }M_i=\bigcup _{i<\delta }N_i$
which is a
![]() $(\xi ,\delta )$
-limit.
$(\xi ,\delta )$
-limit.
Proposition 6.24.
-
1. Let
 $\xi \geq \mu ^+$
,
$\xi \geq \mu ^+$
,
 $\mathbf {K}$
have continuity of
$\mathbf {K}$
have continuity of
 $\xi $
-nonsplitting and be stable in
$\xi $
-nonsplitting and be stable in
 $\xi $
.
$\xi $
.
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\xi $
-superstable iff it is
$\xi $
-superstable iff it is
 $(\xi ,\xi )$
-solvable.
$(\xi ,\xi )$
-solvable. -
2. If
 $\mu>\operatorname {LS}(\mathbf {K})$
and
$\mu>\operatorname {LS}(\mathbf {K})$
and
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(<\mu )$
-tame, then it is
$(<\mu )$
-tame, then it is
 $\mu $
-superstable iff it is
$\mu $
-superstable iff it is
 $(\mu ^+,\mu ^+)$
-solvable.
$(\mu ^+,\mu ^+)$
-solvable.
Proof
-
1. Suppose
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\xi $
-superstable. By Lemma 6.23, superlimits in
$\xi $
-superstable. By Lemma 6.23, superlimits in
 $K_\xi $
are saturated. By Corollary 6.11(2),
$K_\xi $
are saturated. By Corollary 6.11(2),
 $\xi $
-saturated models are closed under chains. By Lemma 6.22, saturated models in
$\xi $
-saturated models are closed under chains. By Lemma 6.22, saturated models in
 $K_\xi $
are superlimits. Therefore, saturated models and superlimits coincide in
$K_\xi $
are superlimits. Therefore, saturated models and superlimits coincide in
 $K_\xi $
. By Fact 6.21, we can define
$K_\xi $
. By Fact 6.21, we can define
 $\operatorname {L}(\mathbf {K'}):=\operatorname {L}(\mathbf {K})$
and
$\operatorname {L}(\mathbf {K'}):=\operatorname {L}(\mathbf {K})$
and
 $ \mathbf {K'}$
to be the class of
$ \mathbf {K'}$
to be the class of
 $\xi $
-saturated models. By Corollary 6.11(2) again, it is an AEC with
$\xi $
-saturated models. By Corollary 6.11(2) again, it is an AEC with
 $\operatorname {LS}(\mathbf {K'})=\xi $
.
$\operatorname {LS}(\mathbf {K'})=\xi $
.The backward direction only requires
 $\xi>\operatorname {LS}(\mathbf {K})$
instead of
$\xi>\operatorname {LS}(\mathbf {K})$
instead of
 $\xi \geq \mu ^+$
: suppose
$\xi \geq \mu ^+$
: suppose
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(\xi ,\xi )$
-solvable. By the proof of Lemma 6.23, superlimits in
$(\xi ,\xi )$
-solvable. By the proof of Lemma 6.23, superlimits in
 $K_\xi $
are saturated and are
$K_\xi $
are saturated and are
 $(\xi ,\delta )$
-limits for
$(\xi ,\delta )$
-limits for
 $\delta <\xi ^+$
. Now given
$\delta <\xi ^+$
. Now given
 $\delta <\xi ^+$
, a u-increasing and continuous chain
$\delta <\xi ^+$
, a u-increasing and continuous chain
 $\langle M_i:i\leq \delta \rangle \subseteq K_\xi $
and
$\langle M_i:i\leq \delta \rangle \subseteq K_\xi $
and
 $p\in \operatorname {gS}(M_\delta )$
, we need to show that p does not
$p\in \operatorname {gS}(M_\delta )$
, we need to show that p does not
 $\xi $
-split over
$\xi $
-split over
 $M_i$
for some
$M_i$
for some
 $i<\delta $
. As
$i<\delta $
. As
 $M_\delta $
is a
$M_\delta $
is a
 $(\xi ,\delta )$
-limit, it is also a superlimit and hence saturated. The conclusion follows from Proposition 6.12.
$(\xi ,\delta )$
-limit, it is also a superlimit and hence saturated. The conclusion follows from Proposition 6.12. -
2. The forward direction combines item (1) and Corollary 6.11(1) (
 $(<\mu )$
-tameness is not needed). Suppose
$(<\mu )$
-tameness is not needed). Suppose
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(\mu ^+,\mu ^+)$
-solvable. By Lemma 6.23 there is a saturated superlimit in
$(\mu ^+,\mu ^+)$
-solvable. By Lemma 6.23 there is a saturated superlimit in
 $K_{\mu ^+}$
, which witnesses the union of saturated models in
$K_{\mu ^+}$
, which witnesses the union of saturated models in
 $K_{\mu ^+}$
is
$K_{\mu ^+}$
is
 $\mu ^+$
-saturated. By Corollary 6.16, it has uniqueness of limit models in
$\mu ^+$
-saturated. By Corollary 6.16, it has uniqueness of limit models in
 $K_{\mu }$
. By
$K_{\mu }$
. By
 $(<\mu )$
-tameness and the proof of Corollary 6.13 (replace “
$(<\mu )$
-tameness and the proof of Corollary 6.13 (replace “
 $\xi $
” there by
$\xi $
” there by
 $\mu $
and “
$\mu $
and “
 $\mu ^+$
” there by
$\mu ^+$
” there by
 ${\operatorname {LS}( \mathbf {K})}^+$
), it is
${\operatorname {LS}( \mathbf {K})}^+$
), it is
 $\mu $
-superstable.
$\mu $
-superstable.
Remark 6.25. One might want to generalize the argument to strictly stable AECs. In that case the statement of Fact 6.21(2) should naturally be for a
![]() $\chi $
-AEC instead of an AEC, but we do not know how to prove that saturated models are closed under
$\chi $
-AEC instead of an AEC, but we do not know how to prove that saturated models are closed under
![]() $\chi $
-directed systems (a similar obstacle is in [Reference Boney, Grossberg, Lieberman, Rosický and Vasey8, Remark 2.3(4)]). On top of that, the equivalence in Fact 6.21 is not clear in that case because we do not have a first-order presentation theorem on
$\chi $
-directed systems (a similar obstacle is in [Reference Boney, Grossberg, Lieberman, Rosický and Vasey8, Remark 2.3(4)]). On top of that, the equivalence in Fact 6.21 is not clear in that case because we do not have a first-order presentation theorem on
![]() $\chi $
-AECs to extract an Ehrenfeucht–Mostowski blueprint (but we do have a
$\chi $
-AECs to extract an Ehrenfeucht–Mostowski blueprint (but we do have a
![]() $(<\mu )$
-ary presentation theorem, see [Reference Boney, Grossberg, Lieberman, Rosický and Vasey8, Theorem 3.2] or [Reference Leung19, Theorem 5.6]).
$(<\mu )$
-ary presentation theorem, see [Reference Boney, Grossberg, Lieberman, Rosický and Vasey8, Theorem 3.2] or [Reference Leung19, Theorem 5.6]).
7 Stability in a tail and U-rank
In this section we look at two characterizations of superstability. For convenience we follow [Reference Vasey38, Section 4] to define some cardinals:
Definition 7.1.
-
1.
 $\lambda (\mathbf {K})$
stands for the first stability cardinal above
$\lambda (\mathbf {K})$
stands for the first stability cardinal above
 $\operatorname {LS}(\mathbf {K})$
.
$\operatorname {LS}(\mathbf {K})$
. -
2.
 $\chi (\mathbf {K})$
stands for the least regular cardinal
$\chi (\mathbf {K})$
stands for the least regular cardinal
 $\delta $
such that
$\delta $
such that
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\delta $
-local character of
$\delta $
-local character of
 $\xi $
-nonsplitting for some stability cardinal
$\xi $
-nonsplitting for some stability cardinal
 $\xi \geq \operatorname {LS}( \mathbf {K})$
.
$\xi \geq \operatorname {LS}( \mathbf {K})$
. -
3.
 $\lambda '(\mathbf {K})$
stands for the minimum stability cardinal
$\lambda '(\mathbf {K})$
stands for the minimum stability cardinal
 $\xi $
such that for any stability cardinal
$\xi $
such that for any stability cardinal
 $\xi '\geq \xi $
,
$\xi '\geq \xi $
,
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\chi (\mathbf {K})$
-local character of
$\chi (\mathbf {K})$
-local character of
 $\xi '$
-nonsplitting.
$\xi '$
-nonsplitting.
Observation 7.2.
-
1. By Assumption 2.1,
 $\lambda (\mathbf {K})\leq \mu $
.
$\lambda (\mathbf {K})\leq \mu $
. -
2. By Definition 3.10 (see also the remark after it),
 $\chi (\mathbf {K})\leq \chi $
.
$\chi (\mathbf {K})\leq \chi $
. -
3. By Lemma 6.7, we can equivalently define
 $\lambda '(\mathbf {K})$
as the minimum stability cardinal
$\lambda '(\mathbf {K})$
as the minimum stability cardinal
 $\xi $
such that
$\xi $
such that
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\chi (\mathbf {K})$
-local character of
$\chi (\mathbf {K})$
-local character of
 $\xi $
-nonsplitting.
$\xi $
-nonsplitting. -
4.
 $\mathbf {K}$
is eventually superstable (
$\mathbf {K}$
is eventually superstable (
 $\xi $
-superstable for large enough
$\xi $
-superstable for large enough
 $\xi $
) iff
$\xi $
) iff
 $\chi ( \mathbf {K})={\aleph _0}$
.
$\chi ( \mathbf {K})={\aleph _0}$
.
Currently we do not have a nice bound of
![]() $\lambda '(\mathbf {K})$
so the cardinal threshold might be very high if we invoke
$\lambda '(\mathbf {K})$
so the cardinal threshold might be very high if we invoke
![]() $\lambda '(\mathbf {K})$
or
$\lambda '(\mathbf {K})$
or
![]() $\chi (\mathbf {K})$
. Vasey built upon [Reference Shelah23] and spent several sections to derive:
$\chi (\mathbf {K})$
. Vasey built upon [Reference Shelah23] and spent several sections to derive:
Fact 7.3 [Reference Vasey38, Theorem 11.3(2)].
Suppose
![]() $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
![]() $\xi $
-nonsplitting for all stability cardinal
$\xi $
-nonsplitting for all stability cardinal
![]() $\xi $
, then
$\xi $
, then
![]() $\lambda '( \mathbf {K})<h(\lambda (\mathbf {K}))$
.
$\lambda '( \mathbf {K})<h(\lambda (\mathbf {K}))$
.
We can now state Vasey’s characterization that superstability is equivalent to stability in a tail of cardinals. Since continuity of
![]() $\mu $
-nonsplitting is not assumed there, item (1) only holds for singular
$\mu $
-nonsplitting is not assumed there, item (1) only holds for singular
![]() $\xi $
. Also, the original formulation wrote
$\xi $
. Also, the original formulation wrote
![]() $\lambda '(\mathbf {K})$
instead of
$\lambda '(\mathbf {K})$
instead of
![]() $(\lambda '(\mathbf {K}))^+$
but the proof did not go through.
$(\lambda '(\mathbf {K}))^+$
but the proof did not go through.
Fact 7.4. Let
![]() $\mathbf {K}$
be
$\mathbf {K}$
be
![]() $\operatorname {LS}(\mathbf {K})$
-tame with a monster model.
$\operatorname {LS}(\mathbf {K})$
-tame with a monster model.
-
1. [Reference Vasey38, Corollary 4.14] Let
 $\chi _1$
as in Fact 6.3,
$\chi _1$
as in Fact 6.3,
 $\xi \geq (\lambda '(\mathbf {K}))^++\chi _1$
be singular,
$\xi \geq (\lambda '(\mathbf {K}))^++\chi _1$
be singular,
 $\mathbf {K}$
be stable in unboundedly many cardinal
$\mathbf {K}$
be stable in unboundedly many cardinal
 $<\xi $
.
$<\xi $
.
 $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
 $\xi $
iff
$\xi $
iff
 $\operatorname {cf}(\xi )\geq \chi (\mathbf {K})$
.
$\operatorname {cf}(\xi )\geq \chi (\mathbf {K})$
. -
2. [Reference Vasey38, Corollary 4.24]
 $\chi (\mathbf {K})={\aleph _0}$
iff
$\chi (\mathbf {K})={\aleph _0}$
iff
 $\mathbf {K}$
is stable in a tail of cardinals.
$\mathbf {K}$
is stable in a tail of cardinals.
We prove a simpler and local analog to Fact 7.4. Rather than looking at the whole tail of cardinals (more accurately the class of singular cardinals with all possible cofinalities) after a potentially high threshold, we directly look for the next
![]() $\omega +1$
many cardinals of
$\omega +1$
many cardinals of
![]() $\mu $
and verify that
$\mu $
and verify that
![]() $\mathbf {K}$
has enough stability, continuity of nonsplitting and symmetry in those cardinals. Symmetry will be guaranteed by more stability.
$\mathbf {K}$
has enough stability, continuity of nonsplitting and symmetry in those cardinals. Symmetry will be guaranteed by more stability.
Proposition 7.5. There is
![]() $\lambda <h(\mu ^{+\omega })$
such that if
$\lambda <h(\mu ^{+\omega })$
such that if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda )$
and has continuity of
$[\mu ,\lambda )$
and has continuity of
![]() $\mu ^{+\omega }$
-nonsplitting, then it is
$\mu ^{+\omega }$
-nonsplitting, then it is
![]() $\mu ^{+\omega }$
-superstable.
$\mu ^{+\omega }$
-superstable.
Proof The forward direction does not depend on
![]() $\lambda $
and is by Corollary 6.11(1) and Proposition 3.16(1). For the backward direction, obtain
$\lambda $
and is by Corollary 6.11(1) and Proposition 3.16(1). For the backward direction, obtain
![]() $\lambda $
from Corollary 6.2(2) and suppose
$\lambda $
from Corollary 6.2(2) and suppose
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda )$
and has continuity of
$[\mu ,\lambda )$
and has continuity of
![]() $\mu ^{+\omega }$
. The conclusion of Corollary 6.2(2) (which uses stability in
$\mu ^{+\omega }$
. The conclusion of Corollary 6.2(2) (which uses stability in
![]() $\mu ^{+\omega }$
and continuity of
$\mu ^{+\omega }$
and continuity of
![]() $\mu ^{+\omega }$
-nonsplitting) gives a saturated model M of size
$\mu ^{+\omega }$
-nonsplitting) gives a saturated model M of size
![]() $\mu ^{+\omega }$
. We show that is a
$\mu ^{+\omega }$
. We show that is a
![]() $(\mu ^{+\omega },\omega )$
-limit: by stability in
$(\mu ^{+\omega },\omega )$
-limit: by stability in
![]() $[\mu ,\mu ^{+\omega })$
, build
$[\mu ,\mu ^{+\omega })$
, build
![]() $\langle M_n:n\leq \omega \rangle \subseteq K_{<\mu ^{+\omega }}$
u-increasing and continuous such that for
$\langle M_n:n\leq \omega \rangle \subseteq K_{<\mu ^{+\omega }}$
u-increasing and continuous such that for
![]() $n<\omega $
,
$n<\omega $
,
![]() $M_n\in K_{\mu ^{+n}}$
and
$M_n\in K_{\mu ^{+n}}$
and
![]() $M_\omega =M$
. On the other hand, by stability in
$M_\omega =M$
. On the other hand, by stability in
![]() $\mu ^{+\omega }$
, build
$\mu ^{+\omega }$
, build
![]() $\langle N_i:i\leq \omega \rangle \subseteq K_{\mu ^{+\omega }}$
u-increasing and continuous such that
$\langle N_i:i\leq \omega \rangle \subseteq K_{\mu ^{+\omega }}$
u-increasing and continuous such that
![]() $M_0\leq N_0$
. By a back-and-forth argument,
$M_0\leq N_0$
. By a back-and-forth argument,
![]() $M\cong _{M_0}N_\omega $
and the latter is a
$M\cong _{M_0}N_\omega $
and the latter is a
![]() $(\mu ^{+\omega },\omega )$
-limit. By uniqueness of limit models of the same cofinality, any
$(\mu ^{+\omega },\omega )$
-limit. By uniqueness of limit models of the same cofinality, any
![]() $(\mu ^{+\omega },\omega )$
-limit is saturated.
$(\mu ^{+\omega },\omega )$
-limit is saturated.
By Proposition 6.12(3) where
![]() $\xi =\mu ^{+\omega }$
,
$\xi =\mu ^{+\omega }$
,
![]() $\delta ={\aleph _0}$
,
$\delta ={\aleph _0}$
,
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
![]() $\mu ^{+\omega }$
-nonsplitting. Together with stability in
$\mu ^{+\omega }$
-nonsplitting. Together with stability in
![]() $\mu ^{+\omega }$
, we know that
$\mu ^{+\omega }$
, we know that
![]() $\mathbf {K}$
is superstable in
$\mathbf {K}$
is superstable in
![]() $\mu ^{+\omega }$
.
$\mu ^{+\omega }$
.
We state a more general form of the above proposition:
Corollary 7.6. Let
![]() $\delta $
be a regular cardinal. There is
$\delta $
be a regular cardinal. There is
![]() $\lambda <h(\mu ^{+\delta })$
such that if
$\lambda <h(\mu ^{+\delta })$
such that if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda )$
and has continuity of
$[\mu ,\lambda )$
and has continuity of
![]() $\mu ^{+\delta }$
-nonsplitting, then it has
$\mu ^{+\delta }$
-nonsplitting, then it has
![]() $\delta $
-local character of
$\delta $
-local character of
![]() $\mu ^{+\delta }$
-nonsplitting. Stability in
$\mu ^{+\delta }$
-nonsplitting. Stability in
![]() $[\mu ,\lambda )$
can be replaced by stability in
$[\mu ,\lambda )$
can be replaced by stability in
![]() $[\mu ^{+\delta },\lambda )$
and unboundedly many cardinals below
$[\mu ^{+\delta },\lambda )$
and unboundedly many cardinals below
![]() $\mu ^{+\delta }$
.
$\mu ^{+\delta }$
.
Proof Replace “
![]() $\omega $
” by
$\omega $
” by
![]() $\delta $
in Proposition 7.5. Notice that unboundedly stability many cardinals below
$\delta $
in Proposition 7.5. Notice that unboundedly stability many cardinals below
![]() $\mu ^{+\delta }$
are sufficient to build
$\mu ^{+\delta }$
are sufficient to build
![]() $\langle M_i:i<\delta \rangle \subseteq K_{<\mu ^{+\delta }}$
u-increasing.
$\langle M_i:i<\delta \rangle \subseteq K_{<\mu ^{+\delta }}$
u-increasing.
Remark 7.7.
-
1. A missing case of Proposition 7.5 is perhaps the regular cardinal
 ${\aleph _0}$
. In [Reference Baldwin, Kueker and VanDieren1, Theorem 2], it was shown that if
${\aleph _0}$
. In [Reference Baldwin, Kueker and VanDieren1, Theorem 2], it was shown that if
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\omega $
-locality,
$\omega $
-locality,
 $\aleph _0$
-tameness and stability in
$\aleph _0$
-tameness and stability in
 ${\aleph _0}$
, then
${\aleph _0}$
, then
 $\mathbf {K}$
is stable everywhere. The original proof used a tree argument of height
$\mathbf {K}$
is stable everywhere. The original proof used a tree argument of height
 $\omega $
. We provide an alternative proof using our general tools: by
$\omega $
. We provide an alternative proof using our general tools: by
 $\omega $
-locality and Proposition 3.16(2),
$\omega $
-locality and Proposition 3.16(2),
 $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
 ${\aleph _0}$
-nonsplitting. By Proposition 3.9,
${\aleph _0}$
-nonsplitting. By Proposition 3.9,
 $\mathbf {K}$
has
$\mathbf {K}$
has
 ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
 ${\aleph _0}$
-nonsplitting. By Corollary 6.11(1), it is (super)stable everywhere.
${\aleph _0}$
-nonsplitting. By Corollary 6.11(1), it is (super)stable everywhere. -
2. Our proof strategy of Proposition 7.5 is similar to that of [Reference Vasey38, Theorem 4.11] but we use different tools. Both assume stability in
 $\mu ^{+\omega }$
and unboundedly many cardinals in
$\mu ^{+\omega }$
and unboundedly many cardinals in
 $\mu ^{+\omega }$
. To obtain a saturated model, Vasey raised the threshold of
$\mu ^{+\omega }$
. To obtain a saturated model, Vasey raised the threshold of
 $\mu $
so that the union of
$\mu $
so that the union of
 $\mu ^{+n}$
-saturated models is
$\mu ^{+n}$
-saturated models is
 $\mu ^{+n}$
-saturated (see Fact 6.3). Then he used an unjustified claim [Reference Vasey38, Theorem 4.13] that models in
$\mu ^{+n}$
-saturated (see Fact 6.3). Then he used an unjustified claim [Reference Vasey38, Theorem 4.13] that models in
 $K_{\mu ^{+\omega }}$
can be closed to a
$K_{\mu ^{+\omega }}$
can be closed to a
 $\mu ^{+n}$
-saturated model (it seems they would invoke [Reference Boney and Vasey11, Theorem 4.30] but we cannot verify this). These two give a saturated model in
$\mu ^{+n}$
-saturated model (it seems they would invoke [Reference Boney and Vasey11, Theorem 4.30] but we cannot verify this). These two give a saturated model in
 $K_{\mu ^{+\omega }}$
. In contrast, we bypass such gap by using the uniqueness of long enough limit models in
$K_{\mu ^{+\omega }}$
. In contrast, we bypass such gap by using the uniqueness of long enough limit models in
 $K_{\mu ^{+\omega }}$
, this immediately gives us a saturated model in
$K_{\mu ^{+\omega }}$
, this immediately gives us a saturated model in
 $K_{\mu ^{+\omega }}$
. After that, Vasey and our approaches converge: the saturated model is a
$K_{\mu ^{+\omega }}$
. After that, Vasey and our approaches converge: the saturated model is a
 $(\mu ^{+\omega },\omega )$
-limit and Proposition 6.12 gives
$(\mu ^{+\omega },\omega )$
-limit and Proposition 6.12 gives
 ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
 $\mu ^{+\omega }$
-nonsplitting.
$\mu ^{+\omega }$
-nonsplitting.
Question 7.8.
-
1. Perhaps under extra assumptions, is it possible to obtain a tighter bound of
 $\lambda '(\mathbf {K})$
in terms of
$\lambda '(\mathbf {K})$
in terms of
 $\lambda (\mathbf {K})$
than in Fact 7.3?
$\lambda (\mathbf {K})$
than in Fact 7.3? -
2. Let
 $\xi _1,\xi _2$
be stability cardinals. Is there any relationship between continuity of
$\xi _1,\xi _2$
be stability cardinals. Is there any relationship between continuity of
 $\xi _1$
-nonsplitting and continuity of
$\xi _1$
-nonsplitting and continuity of
 $\xi _2$
-nonsplitting? Similarly, can one say anything about continuity of
$\xi _2$
-nonsplitting? Similarly, can one say anything about continuity of
 $\xi _1$
-nonsplitting if for unboundedly many stability cardinal
$\xi _1$
-nonsplitting if for unboundedly many stability cardinal
 $\xi <\xi _1$
,
$\xi <\xi _1$
,
 $\mathbf {K}$
has continuity of
$\mathbf {K}$
has continuity of
 $\xi $
-nonsplitting? A positive answer might help improve Proposition 7.5.
$\xi $
-nonsplitting? A positive answer might help improve Proposition 7.5.
In [Reference Boney and Grossberg6, Section 7], Boney and Grossberg developed a U-rank for an independence relation over types of arbitrary length.
Definition 7.9. [Reference Boney and Grossberg6, Definition 7.2] Let
![]() $\mathbf {K}$
have a monster model and an independence relation over types of length one. U is a class function that maps each Galois type (of length one) in the monster model to an ordinal or
$\mathbf {K}$
have a monster model and an independence relation over types of length one. U is a class function that maps each Galois type (of length one) in the monster model to an ordinal or
![]() $\infty $
, such that for any
$\infty $
, such that for any
![]() $M\in K$
,
$M\in K$
,
![]() $p\in \operatorname {gS}(M)$
:
$p\in \operatorname {gS}(M)$
:
-
1.
 $U(p)\geq 0$
.
$U(p)\geq 0$
. -
2. For limit ordinal
 $\alpha $
,
$\alpha $
,
 $U(p)\geq \alpha $
iff
$U(p)\geq \alpha $
iff
 $U(p)\geq \beta $
for all
$U(p)\geq \beta $
for all
 $\beta <\alpha $
.
$\beta <\alpha $
. -
3. For an ordinal
 $\beta $
,
$\beta $
,
 $U(p)\geq \beta +1$
iff there is
$U(p)\geq \beta +1$
iff there is
 $M'\geq M$
,
$M'\geq M$
,
 $\Vert M' \Vert =\Vert M \Vert $
and
$\Vert M' \Vert =\Vert M \Vert $
and
 $p'\in \operatorname {gS}(M')$
such that
$p'\in \operatorname {gS}(M')$
such that
 $p'$
is a nonforking (in the sense of the given independence relation) extension of p and
$p'$
is a nonforking (in the sense of the given independence relation) extension of p and
 $U(p')\geq \beta $
.
$U(p')\geq \beta $
. -
4. For an ordinal
 $\alpha $
,
$\alpha $
,
 $U(p)=\alpha $
iff
$U(p)=\alpha $
iff
 $U(p)\geq \alpha $
but
$U(p)\geq \alpha $
but
 $U(p)\not \geq \alpha +1$
.
$U(p)\not \geq \alpha +1$
. -
5.
 $U(p)=\infty $
iff
$U(p)=\infty $
iff
 $U(p)\geq \alpha $
for all ordinals
$U(p)\geq \alpha $
for all ordinals
 $\alpha $
.
$\alpha $
.
Through a series of lemmas, they managed to obtain the following fact (Assumption 2.1 is not needed).
Fact 7.10 [Reference Boney and Grossberg6, Theorem 7.9].
Let
![]() $\mathbf {K}$
have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Let
$\mathbf {K}$
have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Let
![]() $M\in K$
and
$M\in K$
and
![]() $p\in \operatorname {gS}(M)$
. The following are equivalent:
$p\in \operatorname {gS}(M)$
. The following are equivalent:
-
1.
 $U(p)=\infty $
.
$U(p)=\infty $
. -
2. There is
 $\langle p_n:n<\omega \rangle $
such that
$\langle p_n:n<\omega \rangle $
such that
 $p_0=p$
and for
$p_0=p$
and for
 $n<\omega $
, the domain of
$n<\omega $
, the domain of
 $p_n$
has size
$p_n$
has size
 $\Vert M \Vert $
, and
$\Vert M \Vert $
, and
 $p_{n+1}$
is a forking extension of
$p_{n+1}$
is a forking extension of
 $p_n$
.
$p_n$
.
The original proof proceeds with a lemma followed by the theorem statement. Since the proof of the lemma omitted some details, and that the lemma and the theorem made reference to each other, we straighten the proof as follows:
Lemma 7.11. (2)
![]() $\Rightarrow $
(1) holds in Fact 7.10.
$\Rightarrow $
(1) holds in Fact 7.10.
Proof By induction on each ordinal
![]() $\alpha $
, we show that for each
$\alpha $
, we show that for each
![]() $\alpha $
, for each
$\alpha $
, for each
![]() $n<\omega $
,
$n<\omega $
,
![]() $U(p_n)\geq \alpha $
. The base case
$U(p_n)\geq \alpha $
. The base case
![]() $\alpha =0$
is by the definition of U. The limit case follows from the inductive hypothesis. Suppose we have proven the case
$\alpha =0$
is by the definition of U. The limit case follows from the inductive hypothesis. Suppose we have proven the case
![]() $\alpha $
, then for each
$\alpha $
, then for each
![]() $n<\omega $
, inductive hypothesis gives
$n<\omega $
, inductive hypothesis gives
![]() $U(p_{n+1})\geq \alpha $
. By the definition of U,
$U(p_{n+1})\geq \alpha $
. By the definition of U,
![]() $U(p_n)\geq \alpha +1$
.
$U(p_n)\geq \alpha +1$
.
Lemma 7.12. Let
![]() $\mathbf {K}$
have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Let
$\mathbf {K}$
have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Let
![]() $\lambda \geq \operatorname {LS}(\mathbf {K})$
. There is an ordinal
$\lambda \geq \operatorname {LS}(\mathbf {K})$
. There is an ordinal
![]() $\alpha _\lambda <(2^\lambda )^+$
such that for
$\alpha _\lambda <(2^\lambda )^+$
such that for
![]() $M\in K_\lambda $
,
$M\in K_\lambda $
,
![]() $p\in \operatorname {gS}(M)$
, if
$p\in \operatorname {gS}(M)$
, if
![]() $U(p)\geq \alpha _\lambda $
then
$U(p)\geq \alpha _\lambda $
then
![]() $U(p)=\infty $
.
$U(p)=\infty $
.
Proof By invariance, there are at most
![]() $2^\lambda $
many U-ranks of types over models of size
$2^\lambda $
many U-ranks of types over models of size
![]() $\lambda $
. It suffices to show that there is no gap in the U-rank: if
$\lambda $
. It suffices to show that there is no gap in the U-rank: if
![]() $\beta $
is an ordinal,
$\beta $
is an ordinal,
![]() $N\in K_\lambda $
,
$N\in K_\lambda $
,
![]() $q\in \operatorname {gS}(N)$
with
$q\in \operatorname {gS}(N)$
with
![]() $\beta <U(q)<\infty $
, then there is a forking extension
$\beta <U(q)<\infty $
, then there is a forking extension
![]() $q'$
of q (with domain of size
$q'$
of q (with domain of size
![]() $\lambda $
) such that
$\lambda $
) such that
![]() $U(q')=\beta $
. Otherwise pick a counterexample
$U(q')=\beta $
. Otherwise pick a counterexample
![]() $q\in \operatorname {gS}(N)$
. Since
$q\in \operatorname {gS}(N)$
. Since
![]() $U(q)\geq \beta +1$
, there is a forking extension
$U(q)\geq \beta +1$
, there is a forking extension
![]() $q_1$
of q such that
$q_1$
of q such that
![]() $U(q_1)\geq \beta $
. As
$U(q_1)\geq \beta $
. As
![]() $U(q_1)$
cannot be
$U(q_1)$
cannot be
![]() $\beta $
,
$\beta $
,
![]() $U(q_1)\geq \beta +1$
. Using monotonicity of forking, we can inductively build
$U(q_1)\geq \beta +1$
. Using monotonicity of forking, we can inductively build
![]() $\langle q_n:n<\omega \rangle $
with
$\langle q_n:n<\omega \rangle $
with
![]() $q_0:= q$
and for
$q_0:= q$
and for
![]() $n<\omega $
,
$n<\omega $
,
![]() $q_{n+1}$
is a forking extension of
$q_{n+1}$
is a forking extension of
![]() $q_n$
. By Lemma 7.11,
$q_n$
. By Lemma 7.11,
![]() $U(q_0)=U(q)=\infty $
, contradicting the assumption on
$U(q_0)=U(q)=\infty $
, contradicting the assumption on
![]() $U(q)$
.
$U(q)$
.
Lemma 7.13. Let
![]() $\mathbf {K}$
have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Then (1)
$\mathbf {K}$
have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Then (1)
![]() $\Rightarrow $
(2) in Fact 7.10 holds.
$\Rightarrow $
(2) in Fact 7.10 holds.
Proof Let
![]() $\alpha _\lambda $
as in Lemma 7.12 and
$\alpha _\lambda $
as in Lemma 7.12 and
![]() $p_0:= p$
. Define
$p_0:= p$
. Define
![]() $\langle p_n:n<\omega \rangle $
inductively such that
$\langle p_n:n<\omega \rangle $
inductively such that
![]() $U(p_n)=\infty $
. The base case is by assumption on p. Suppose
$U(p_n)=\infty $
. The base case is by assumption on p. Suppose
![]() $p_n$
is constructed with
$p_n$
is constructed with
![]() $U(p_n)=\infty $
, then in particular
$U(p_n)=\infty $
, then in particular
![]() $U(p_n)\geq \alpha _\lambda +1$
. By definition of U, there is a forking extension
$U(p_n)\geq \alpha _\lambda +1$
. By definition of U, there is a forking extension
![]() $p_{n+1}$
of
$p_{n+1}$
of
![]() $p_n$
(with domain of size
$p_n$
(with domain of size
![]() $\lambda $
) such that
$\lambda $
) such that
![]() $U(p_{n+1})\geq \alpha _\lambda $
. By Lemma 7.12 again,
$U(p_{n+1})\geq \alpha _\lambda $
. By Lemma 7.12 again,
![]() $U(p_{n+1})=\infty $
.
$U(p_{n+1})=\infty $
.
We have now arrived at an alternative characterization of superstability. At the end of [Reference Grossberg and Vasey18, Section 6], they suggested the use of coheir and show that superstability implies bounded U-rank. Since we cannot verify the claim, we use instead
![]() $\mu $
-nonforking as the independence relation to characterize superstability as bounded U-rank for limit models in
$\mu $
-nonforking as the independence relation to characterize superstability as bounded U-rank for limit models in
![]() $K_{\mu }$
.
$K_{\mu }$
.
Corollary 7.14. Under Assumption 2.1, restrict
![]() $\mu $
-nonforking to limit models in
$\mu $
-nonforking to limit models in
![]() $K_{\mu }$
ordered by
$K_{\mu }$
ordered by
![]() $\leq _u$
. Then
$\leq _u$
. Then
![]() $ \mathbf {K}$
is
$ \mathbf {K}$
is
![]() $\mu $
-superstable iff
$\mu $
-superstable iff
![]() $U(p)<\infty $
for all
$U(p)<\infty $
for all
![]() $p\in \operatorname {gS}(M)$
and limit model
$p\in \operatorname {gS}(M)$
and limit model
![]() $M\in K_{\mu }$
.
$M\in K_{\mu }$
.
Proof By Fact 7.10, we need to show
![]() $\mu $
-superstability is equivalent to the negation of criterion (2) there. By continuity of
$\mu $
-superstability is equivalent to the negation of criterion (2) there. By continuity of
![]() $\mu $
-nonforking Proposition 4.4 and the proof of Lemma 3.7, it suffices to prove that
$\mu $
-nonforking Proposition 4.4 and the proof of Lemma 3.7, it suffices to prove that
![]() $\mu $
-superstability is equivalent to
$\mu $
-superstability is equivalent to
![]() $\mu $
-nonforking having local character
$\mu $
-nonforking having local character
![]() ${\aleph _0}$
(under
${\aleph _0}$
(under
![]() $AP$
it is always possible to extend an omega-chain of types). The forward direction is given by Proposition 4.9 and the backward direction is given by Proposition 4.2, Proposition 4.5, and Proposition 4.19.
$AP$
it is always possible to extend an omega-chain of types). The forward direction is given by Proposition 4.9 and the backward direction is given by Proposition 4.2, Proposition 4.5, and Proposition 4.19.
We look at one more result of U-rank, which shows the equivalence of being a nonforking extension and having the same U-rank (Fact 7.16). The extra assumption of
![]() $\operatorname {LS}(\mathbf {K})$
-witness property for singletons is pointed out by [Reference Grossberg and Mazari-Armida15, Lemma 8.8] to allow the proof of monotonicity of U-rank [Reference Boney and Grossberg6, Lemma 7.3] to go through. We will adapt their definition of
$\operatorname {LS}(\mathbf {K})$
-witness property for singletons is pointed out by [Reference Grossberg and Mazari-Armida15, Lemma 8.8] to allow the proof of monotonicity of U-rank [Reference Boney and Grossberg6, Lemma 7.3] to go through. We will adapt their definition of
![]() $\operatorname {LS}(\mathbf {K})$
-witness property for singletons because our nonforking is originally defined for model-domains while their independence relations assume set-domains (another approach is perhaps to work in the closure (Definition 7.17) of nonforking, but we will not pursue it here).
$\operatorname {LS}(\mathbf {K})$
-witness property for singletons because our nonforking is originally defined for model-domains while their independence relations assume set-domains (another approach is perhaps to work in the closure (Definition 7.17) of nonforking, but we will not pursue it here).
Definition 7.15.
-
1. Let
 $\lambda $
be a cardinal. An independence relation
$\lambda $
be a cardinal. An independence relation
 has the
has the
 $\lambda $
-witness property if the following holds: let a be a singleton and
$\lambda $
-witness property if the following holds: let a be a singleton and
 $M,N\in K$
. If for any
$M,N\in K$
. If for any
 $M'$
with
$M'$
with
 $M\leq M'\leq N$
,
$M\leq M'\leq N$
,
 $\Vert M' \Vert \leq \Vert M \Vert +\lambda $
, we have
$\Vert M' \Vert \leq \Vert M \Vert +\lambda $
, we have
 , then
, then
 .
. -
2. An independence relation satisfies left transitivity if the following holds: let A be a set,
 $M_0\leq M_1\leq N$
with
$M_0\leq M_1\leq N$
with
 and
and
 , then
, then
 .
.
Fact 7.16 [Reference Boney and Grossberg6, Theorem 7.7].
Let
![]() $\mathbf {K}$
have a monster model and an independence relation over types of arbitrary length. Suppose the independence relation satisfies: invariance, monotonicity, left transitivity, existence, extension, uniqueness, symmetry and
$\mathbf {K}$
have a monster model and an independence relation over types of arbitrary length. Suppose the independence relation satisfies: invariance, monotonicity, left transitivity, existence, extension, uniqueness, symmetry and
![]() $\operatorname {LS}(\mathbf {K})$
-witness property for singletons. For any
$\operatorname {LS}(\mathbf {K})$
-witness property for singletons. For any
![]() $p\in \operatorname {gS}(M)$
, any
$p\in \operatorname {gS}(M)$
, any
![]() $q\in \operatorname {gS}(M_1)$
extending p such that both
$q\in \operatorname {gS}(M_1)$
extending p such that both
![]() $U(p),U(q)<\infty $
, then
$U(p),U(q)<\infty $
, then
We notice a gap in [Reference Boney and Grossberg6, Lemma 7.6] which Fact 7.16 depends on (readers can skip after the proof of Proposition 7.19 if they simply use Fact 7.16 as a blackbox). As usual, their definition of independence relations assume that the domain contains the base: if we write
![]() , we assume
, we assume
![]() $M\leq N$
. In the proof of [Reference Boney and Grossberg6, Lemma 7.6], they applied monotonicity to obtain
$M\leq N$
. In the proof of [Reference Boney and Grossberg6, Lemma 7.6], they applied monotonicity to obtain
![]() . However,
. However,
![]() $\bar {N_0}\not \leq N_1$
because
$\bar {N_0}\not \leq N_1$
because
![]() $c\in \bar {N_0}-N_1$
might happen. We will rewrite the proof in Proposition 7.19 using the idea of a closure of an independence relation, and drawing results from [Reference Boney, Grossberg, Kolesnikov and Vasey7].
$c\in \bar {N_0}-N_1$
might happen. We will rewrite the proof in Proposition 7.19 using the idea of a closure of an independence relation, and drawing results from [Reference Boney, Grossberg, Kolesnikov and Vasey7].
Definition 7.17 [Reference Boney, Grossberg, Kolesnikov and Vasey7, Definition 3.4].
![]() is a closure of an independence relation
is a closure of an independence relation
![]() if it satisfies the following properties:
if it satisfies the following properties:
-
1.
 is defined on triples of the form
is defined on triples of the form
 $(A,M,B)$
where
$(A,M,B)$
where
 $M\in K$
, A and B are sets of elements. We allow
$M\in K$
, A and B are sets of elements. We allow
 $M\not \subseteq B$
.
$M\not \subseteq B$
. -
2. Invariance: if
 $f\in \operatorname {Aut}(\mathfrak {C})$
and
$f\in \operatorname {Aut}(\mathfrak {C})$
and
 , then
, then
 .
. -
3. Monotonicity: if
 ,
,
 $A'\subseteq A$
,
$A'\subseteq A$
,
 $B'\subseteq B$
, then
$B'\subseteq B$
, then
 .
. -
4. Base monotonicity: if
 and
and
 $M\leq M'\subseteq M\cup B$
, then
$M\leq M'\subseteq M\cup B$
, then
 .
.
The minimal closure of
![]() (which is the smallest closure of
(which is the smallest closure of
![]() ) is defined by:
) is defined by:
![]() iff there is
iff there is
![]() $N\geq M$
,
$N\geq M$
,
![]() $N\supseteq C$
such that
$N\supseteq C$
such that
![]() .
.
We quote the following lemma without proof.
Lemma 7.18 [Reference Boney, Grossberg, Kolesnikov and Vasey7, Lemma 5.4].
Let
![]() be an independence relation for types of arbitrary length,
be an independence relation for types of arbitrary length,
![]() be the minimal closure of
be the minimal closure of
![]() .
.
-
1.
 has symmetry iff
has symmetry iff
 has symmetry.
has symmetry. -
2. Suppose
 has existence, extension. Then
has existence, extension. Then
 has left transitivity iff
has left transitivity iff
 does.
does.
Proposition 7.19. Under the same hypothesis as Fact 7.10, let
![]() $N_0\leq N_1\leq \bar {N_1}$
;
$N_0\leq N_1\leq \bar {N_1}$
;
![]() $N_0\leq \bar {N_0}\leq \bar {N_1}$
;
$N_0\leq \bar {N_0}\leq \bar {N_1}$
;
![]() $N_0\leq N_2$
;
$N_0\leq N_2$
;
![]() $c\in |N_0|$
. If
$c\in |N_0|$
. If
then there is some
![]() $N_3$
extending both
$N_3$
extending both
![]() $N_1$
and
$N_1$
and
![]() $N_2$
such that
$N_2$
such that
Proof We write
to mean the minimal closure of the given independence relation
. By symmetry twice on
, there is
![]() $\bar {N_2}$
containing c and extending
$\bar {N_2}$
containing c and extending
![]() $\bar {N_0},N_2$
such that
$\bar {N_0},N_2$
such that
. By definition of the minimal closure,

On the other hand, by symmetry (and monotonicity) on
,
. Then
. Applying Lemma 7.18(2) to the last two closure independence, we have
. By Lemma 7.18(1), there is
![]() $N_3'\geq N_2$
and containing c such that
$N_3'\geq N_2$
and containing c such that
. By definition of the minimal closure,
. (Here we return to the original proof.) By base monotonicity,
. By symmetry, there is
![]() $N_3$
extending
$N_3$
extending
![]() $N_1$
and
$N_1$
and
![]() $N_2$
such that
$N_2$
such that
. By monotonicity,
as desired.
Back to Fact 7.16, we would like to know if there are any examples of independence relations that satisfy its hypotheses. The approach in [Reference Boney and Grossberg6] is to consider coheir [Reference Boney and Grossberg6, Definition 3.2], assuming tameness, shortness, no weak order property and that coheir satisfies extension. More developments of coheir can be found in [Reference Vasey32] but the framework there is too abstract to handle. Another natural candidate is
![]() $\mu $
-nonforking. The obstacle is that the hypotheses require the independence relation to be over types of arbitrary length, so the properties required (say symmetry) are stronger. In the following, we will use known results to extend
$\mu $
-nonforking. The obstacle is that the hypotheses require the independence relation to be over types of arbitrary length, so the properties required (say symmetry) are stronger. In the following, we will use known results to extend
![]() $\mu $
-nonforking to longer types.
$\mu $
-nonforking to longer types.
We state the full assumptions of the following facts.
Fact 7.20. Let
![]() $\mathbf {K}$
have a monster model,
$\mathbf {K}$
have a monster model,
![]() $\lambda \geq \operatorname {LS}(\mathbf {K})$
.
$\lambda \geq \operatorname {LS}(\mathbf {K})$
.
-
1. [Reference Boney and Vasey12, Theorem 1.1] Suppose
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $\lambda $
-tame and there is a good
$\lambda $
-tame and there is a good
 $(\geq \lambda )$
-frame perhaps except the symmetry property. Then the frame can be extended to a good frame for types of arbitrary length and satisfying symmetry.
$(\geq \lambda )$
-frame perhaps except the symmetry property. Then the frame can be extended to a good frame for types of arbitrary length and satisfying symmetry. -
2. [Reference Boney, Grossberg, Kolesnikov and Vasey7, Lemma 5.9] Let
 be an independence relation for types of arbitrary length. Suppose
be an independence relation for types of arbitrary length. Suppose
 satisfies symmetry and right transitivity, then it satisfies left transitivity.
satisfies symmetry and right transitivity, then it satisfies left transitivity.
Remark 7.21.
-
1. The way that [Reference Boney and Vasey12, Definition 4.1] extends a good frame to longer types is via “independent sequences.” In general the extended frame is not necessarily type-full (existence holds for independent sequences only). However, our original
 $\mu $
-nonforking for singletons is type-full and we start from singletons as input for the U-rank, so our argument goes through.
$\mu $
-nonforking for singletons is type-full and we start from singletons as input for the U-rank, so our argument goes through. -
2. If we simply extend nonsplitting of singletons to nonsplitting of longer types (allowing
 $p\in \operatorname {gS}^{<\infty }(N)$
in Definition 3.2), then it changes the definition of nonforking and many results do not generalize (stability of
$p\in \operatorname {gS}^{<\infty }(N)$
in Definition 3.2), then it changes the definition of nonforking and many results do not generalize (stability of
 $\mu $
-types in
$\mu $
-types in
 $K_{\mu }$
immediately fails).
$K_{\mu }$
immediately fails).
We can now derive an independence relation that satisfies the hypotheses of Fact 7.16 under
![]() $\mu $
-superstability. We will use Assumption 2.1.
$\mu $
-superstability. We will use Assumption 2.1.
Proposition 7.22. Let
![]() $\mathbf {K}$
be
$\mathbf {K}$
be
![]() $\mu $
-superstable. Let
$\mu $
-superstable. Let
![]() $\mathbf {K'}$
be the AEC of the limit models in
$\mathbf {K'}$
be the AEC of the limit models in
![]() $K_{\geq \mu }$
ordered by
$K_{\geq \mu }$
ordered by
![]() $\leq _u$
. Then
$\leq _u$
. Then
![]() $\mu $
-nonforking restricted to
$\mu $
-nonforking restricted to
![]() $\mathbf {K'}$
can be extended to a good frame for types of arbitrary length. Also it satisfies left transitivity and
$\mathbf {K'}$
can be extended to a good frame for types of arbitrary length. Also it satisfies left transitivity and
![]() $\mu $
-witness property for singletons.
$\mu $
-witness property for singletons.
Proof By Corollary 4.13 and Remark 4.14(2),
![]() $\mu $
-nonforking restricted to
$\mu $
-nonforking restricted to
![]() $\mathbf {K'}$
forms a good (
$\mathbf {K'}$
forms a good (
![]() $\geq \mu $
)-frame perhaps except symmetry (it actually satisfies symmetry by Corollary 5.13(2) but we do not need this result here).
$\geq \mu $
)-frame perhaps except symmetry (it actually satisfies symmetry by Corollary 5.13(2) but we do not need this result here).
![]() $\mathbf {K'}$
is also
$\mathbf {K'}$
is also
![]() $\mu $
-tame because
$\mu $
-tame because
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\mu $
-tame under Assumption 2.1 and we can extend a model in
$\mu $
-tame under Assumption 2.1 and we can extend a model in
![]() $K_{\mu }$
to a limit model which is in
$K_{\mu }$
to a limit model which is in
![]() $K'$
. By Fact 7.20(1),
$K'$
. By Fact 7.20(1),
![]() $\mu $
-nonforking can be extended to a good
$\mu $
-nonforking can be extended to a good
![]() $(\geq \mu )$
-frame for types of arbitrary length.
$(\geq \mu )$
-frame for types of arbitrary length.
Since the extended frame enjoys symmetry and right transitivity, by Fact 7.20(2) it satisfies left transitivity. We check the
![]() $\mu $
-witness property for singletons: let
$\mu $
-witness property for singletons: let
![]() $M\leq _uN$
both in
$M\leq _uN$
both in
![]() $K'$
,
$K'$
,
![]() $p\in \operatorname {gS}(N)$
. Suppose for any
$p\in \operatorname {gS}(N)$
. Suppose for any
![]() $M'$
with
$M'$
with
![]() $M\leq _u M'\leq _u N$
,
$M\leq _u M'\leq _u N$
,
![]() $\Vert M' \Vert \leq \Vert M \Vert +\mu =\Vert M \Vert $
, we have
$\Vert M' \Vert \leq \Vert M \Vert +\mu =\Vert M \Vert $
, we have
![]() $p\restriction N'$
does not
$p\restriction N'$
does not
![]() $\mu $
-fork over M. We need to show that p does not
$\mu $
-fork over M. We need to show that p does not
![]() $\mu $
-fork over M. Without loss of generality assume
$\mu $
-fork over M. Without loss of generality assume
![]() $\Vert N \Vert>\Vert M \Vert $
. By existence of
$\Vert N \Vert>\Vert M \Vert $
. By existence of
![]() $\mu $
-nonsplitting (Proposition 3.12), there is
$\mu $
-nonsplitting (Proposition 3.12), there is
![]() $N'\in K$
,
$N'\in K$
,
![]() $N'\leq N$
such that p does not
$N'\leq N$
such that p does not
![]() $\mu $
-split over
$\mu $
-split over
![]() $N'$
. As N is saturated (replace “
$N'$
. As N is saturated (replace “
![]() $\mu $
” by
$\mu $
” by
![]() $\Vert N \Vert $
in Corollary 6.2(2)), we can obtain
$\Vert N \Vert $
in Corollary 6.2(2)), we can obtain
![]() $N"\in K^{\prime }_{\Vert M \Vert }$
such that
$N"\in K^{\prime }_{\Vert M \Vert }$
such that
![]() $N'<_uN"<_uN$
and
$N'<_uN"<_uN$
and
![]() $M\leq _uN"$
. By definition p does not
$M\leq _uN"$
. By definition p does not
![]() $\mu $
-fork over
$\mu $
-fork over
![]() $N"$
. Since
$N"$
. Since
![]() $p\restriction N"$
does not
$p\restriction N"$
does not
![]() $\mu $
-fork over M by assumption, Corollary 4.8 guarantees that p does not
$\mu $
-fork over M by assumption, Corollary 4.8 guarantees that p does not
![]() $\mu $
-fork over M.
$\mu $
-fork over M.
Corollary 7.23. Let
![]() $\mathbf {K}$
be
$\mathbf {K}$
be
![]() $\mu $
-superstable, and let
$\mu $
-superstable, and let
![]() $\mathbf {K'}$
be the AEC of the limit models in
$\mathbf {K'}$
be the AEC of the limit models in
![]() $K_{\geq \mu }$
ordered by
$K_{\geq \mu }$
ordered by
![]() $\leq _u$
. Let
$\leq _u$
. Let
![]() be the extended frame from Proposition 7.22 and define the U-rank for
be the extended frame from Proposition 7.22 and define the U-rank for
![]() . For any
. For any
![]() $M<_uM_1\in K'$
,
$M<_uM_1\in K'$
,
![]() $p\in \operatorname {gS}(M)$
, any
$p\in \operatorname {gS}(M)$
, any
![]() $q\in \operatorname {gS}(M_1)$
extending p such that both
$q\in \operatorname {gS}(M_1)$
extending p such that both
![]() $U(p),U(q)<\infty $
, then
$U(p),U(q)<\infty $
, then
8 The main theorems and applications
We summarize our results in two main theorems. The first one concerns stable AECs while the second one concerns superstable ones. Some of the following items allow
![]() $\mu \geq \operatorname {LS}(\mathbf {K})$
but we assume
$\mu \geq \operatorname {LS}(\mathbf {K})$
but we assume
![]() $\mu>\operatorname {LS}(\mathbf {K})$
for a uniform statement. The proofs will come after the main theorems.
$\mu>\operatorname {LS}(\mathbf {K})$
for a uniform statement. The proofs will come after the main theorems.
Main Theorem 8.1. Let
![]() $\mathbf {K}$
be an AEC with a monster model,
$\mathbf {K}$
be an AEC with a monster model,
![]() $\mu>\operatorname {LS}(\mathbf {K})$
,
$\mu>\operatorname {LS}(\mathbf {K})$
,
![]() $\delta \leq \mu $
both be regular. Suppose
$\delta \leq \mu $
both be regular. Suppose
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\mu $
-tame, stable in
$\mu $
-tame, stable in
![]() $\mu $
and has continuity of
$\mu $
and has continuity of
![]() $\mu $
-nonsplitting. The following statements are equivalent under extra assumptions specified after the list:
$\mu $
-nonsplitting. The following statements are equivalent under extra assumptions specified after the list:
-
1.
 $\mathbf {K}$
has
$\mathbf {K}$
has
 $\delta $
-local character of
$\delta $
-local character of
 $\mu $
-nonsplitting.
$\mu $
-nonsplitting. -
2. There is a good frame over the skeleton of
 $(\mu ,\geq \delta )$
-limit models ordered by
$(\mu ,\geq \delta )$
-limit models ordered by
 $\leq _u$
, except for symmetry and local character
$\leq _u$
, except for symmetry and local character
 $\delta $
in place of
$\delta $
in place of
 ${\aleph _0}$
. In this case the frame is canonical.
${\aleph _0}$
. In this case the frame is canonical. -
3.
 $\mathbf {K}$
has uniqueness of
$\mathbf {K}$
has uniqueness of
 $(\mu ,\geq \delta )$
-limit models.
$(\mu ,\geq \delta )$
-limit models. -
4. For any increasing chain of
 $\mu ^+$
-saturated models, if the length of the chain has cofinality
$\mu ^+$
-saturated models, if the length of the chain has cofinality
 $\geq \delta $
, then the union is also
$\geq \delta $
, then the union is also
 $\mu ^+$
-saturated.
$\mu ^+$
-saturated. -
5.
 $K_{\mu ^+}$
has a
$K_{\mu ^+}$
has a
 $\delta $
-superlimit.
$\delta $
-superlimit.
(1) and (2) are equivalent. If
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $(<\mu )$
-tame, then (3) implies (1). There is
$(<\mu )$
-tame, then (3) implies (1). There is
![]() $\lambda _1<h(\mu )$
such that if
$\lambda _1<h(\mu )$
such that if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda _1)$
, then (1) implies (3). Given any
$[\mu ,\lambda _1)$
, then (1) implies (3). Given any
![]() $\zeta \geq \mu ^+$
, stability in
$\zeta \geq \mu ^+$
, stability in
![]() $[\mu ,\lambda _1)$
can be replaced by stability in
$[\mu ,\lambda _1)$
can be replaced by stability in
![]() $[\mu ,\zeta )$
plus no
$[\mu ,\zeta )$
plus no
![]() $\mu $
-order property of length
$\mu $
-order property of length
![]() $\zeta $
.
$\zeta $
.
There is
![]() $\lambda _2<h(\mu ^+)$
such that if
$\lambda _2<h(\mu ^+)$
such that if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ^+,\lambda _2)$
and has continuity of
$[\mu ^+,\lambda _2)$
and has continuity of
![]() $\mu ^+$
-nonsplitting, then (1) implies (4). Given any
$\mu ^+$
-nonsplitting, then (1) implies (4). Given any
![]() $\zeta \geq \mu ^{++}$
, stability in
$\zeta \geq \mu ^{++}$
, stability in
![]() $[\mu ^+,\lambda _2)$
can be replaced by stability in
$[\mu ^+,\lambda _2)$
can be replaced by stability in
![]() $[\mu ^+,\zeta )$
plus no
$[\mu ^+,\zeta )$
plus no
![]() $\mu ^+$
-order property of length
$\mu ^+$
-order property of length
![]() $\zeta $
. Always (4) and (5) are equivalent and they imply (3).
$\zeta $
. Always (4) and (5) are equivalent and they imply (3).
The following diagram summarizes the implications in Main Theorem 8.1. Labels on the arrows indicate the extra assumptions needed, in addition to a monster model,
![]() $\mu $
-tameness, stability in
$\mu $
-tameness, stability in
![]() $\mu $
and continuity of
$\mu $
and continuity of
![]() $\mu $
-nonsplitting. As in the theorem statement, whenever we require stability in the form
$\mu $
-nonsplitting. As in the theorem statement, whenever we require stability in the form
![]() $[\xi ,\lambda )$
, we can replace it by stability in
$[\xi ,\lambda )$
, we can replace it by stability in
![]() $[\xi ,\zeta )$
plus no
$[\xi ,\zeta )$
plus no
![]() $\xi $
-order property of length
$\xi $
-order property of length
![]() $\zeta $
.
$\zeta $
.

Main Theorem 8.2. Let
![]() $\mathbf {K}$
be an AEC with a monster model,
$\mathbf {K}$
be an AEC with a monster model,
![]() $\mu>\operatorname {LS}(\mathbf {K})$
and
$\mu>\operatorname {LS}(\mathbf {K})$
and
![]() $\delta $
be a regular cardinal
$\delta $
be a regular cardinal
![]() $\leq \mu $
. Suppose
$\leq \mu $
. Suppose
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\mu $
-tame, stable in
$\mu $
-tame, stable in
![]() $\mu $
and has continuity of
$\mu $
and has continuity of
![]() $\mu $
-nonsplitting. The following statements are equivalent modulo
$\mu $
-nonsplitting. The following statements are equivalent modulo
![]() $(<\mu )$
-tameness and a jump in cardinal (specified after the list):
$(<\mu )$
-tameness and a jump in cardinal (specified after the list):
-
1.
 $\mathbf {K}$
has
$\mathbf {K}$
has
 ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
 $\mu $
-nonsplitting.
$\mu $
-nonsplitting. -
2. There is a good frame over the limit models in
 $K_{\mu }$
ordered by
$K_{\mu }$
ordered by
 $\leq _u$
, except for symmetry. In this case the frame is canonical.
$\leq _u$
, except for symmetry. In this case the frame is canonical. -
3.
 $K_{\mu }$
has uniqueness of limit models.
$K_{\mu }$
has uniqueness of limit models. -
4. For any increasing chain of
 $\mu ^+$
-saturated models, the union of the chain is also
$\mu ^+$
-saturated models, the union of the chain is also
 $\mu ^+$
-saturated.
$\mu ^+$
-saturated. -
5.
 $K_{\mu ^+}$
has a superlimit.
$K_{\mu ^+}$
has a superlimit. -
6.
 $\mathbf {K}$
is
$\mathbf {K}$
is
 $(\mu ^+,\mu ^+)$
-solvable.
$(\mu ^+,\mu ^+)$
-solvable. -
7.
 $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
 $\geq \mu $
and has continuity of
$\geq \mu $
and has continuity of
 $\mu ^{+\omega }$
-nonsplitting.
$\mu ^{+\omega }$
-nonsplitting. -
8. U-rank is bounded when
 $\mu $
-nonforking is restricted to the limit models in
$\mu $
-nonforking is restricted to the limit models in
 $K_{\mu }$
ordered by
$K_{\mu }$
ordered by
 $\leq _u$
.
$\leq _u$
.
(1), (2), and (8) are equivalent and each of them implies (3) and (4). If
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $(<\mu )$
-tame, then (3) implies (1). Always (4) and (5) are equivalent and they imply (3). (1) implies (6) and (7) while (6) implies (4). (7) implies
$(<\mu )$
-tame, then (3) implies (1). Always (4) and (5) are equivalent and they imply (3). (1) implies (6) and (7) while (6) implies (4). (7) implies
![]() $(1)_{\mu ^{+\omega }}$
:
$(1)_{\mu ^{+\omega }}$
:
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
![]() $\mu ^{+\omega }$
-nonsplitting.
$\mu ^{+\omega }$
-nonsplitting.
The jump in cardinal is due to the lack of a precise bound on
![]() $\lambda '(\mathbf {K})$
in deducing (7)
$\lambda '(\mathbf {K})$
in deducing (7)
![]() $\Rightarrow $
(1) (see Question 7.8(1)). The following diagram summarizes the implications in Main Theorem 8.2. “
$\Rightarrow $
(1) (see Question 7.8(1)). The following diagram summarizes the implications in Main Theorem 8.2. “
![]() $\mu ^{+\omega }$
” indicates the jump in cardinal.
$\mu ^{+\omega }$
” indicates the jump in cardinal.

Proof of Main Theorem 8.1
(1) and (2) are equivalent by Corollary 4.13 and Proposition 4.19. The canonicity of the frame is by Proposition 4.18. Suppose (3) holds. Then the proof of Corollary 6.2(2) and Proposition 6.12(1) give (1).
Suppose (1) holds. Obtain
![]() $\lambda _1=\lambda $
from Corollary 6.2 and take
$\lambda _1=\lambda $
from Corollary 6.2 and take
![]() $\chi =\delta $
. If
$\chi =\delta $
. If
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $[\mu ,\lambda _1)$
, then it has uniqueness of
$[\mu ,\lambda _1)$
, then it has uniqueness of
![]() $(\mu ,\geq \delta )$
-limit models, so (3) holds. The alternative hypotheses of stability and no-order-property work because we can replace
$(\mu ,\geq \delta )$
-limit models, so (3) holds. The alternative hypotheses of stability and no-order-property work because we can replace
![]() $\lambda $
in the proof of Proposition 5.9 by
$\lambda $
in the proof of Proposition 5.9 by
![]() $\zeta $
.
$\zeta $
.
The direction of (1)–(4) is by Proposition 6.6. The alternative hypotheses work because we can replace
![]() $\lambda $
in the proof of Proposition 5.9 by
$\lambda $
in the proof of Proposition 5.9 by
![]() $\zeta $
. (4) and (5) are equivalent by Lemma 6.22 and Lemma 6.23. They imply (3) by Corollary 6.16.
$\zeta $
. (4) and (5) are equivalent by Lemma 6.22 and Lemma 6.23. They imply (3) by Corollary 6.16.
For the proof of Main Theorem 8.2, we show the additional directions and refer the readers to the proof of Main Theorem 8.1 for the original directions.
Proof of Main Theorem 8.2
Compared to Main Theorem 8.1, we do not need the extra stability and continuity of nonsplitting assumptions because superstability already implies them (Corollary 6.11(1) and Proposition 3.16(1)). (1) and (8) are equivalent by Corollary 7.14. (1) implies (7) by Corollary 6.11(1) while (1) implies (6) by the forward direction of Proposition 6.24(2). (6) plus
![]() $(<\mu )$
-tameness implies (4) by the proof of the backward direction of Proposition 6.24(2). (7) implies
$(<\mu )$
-tameness implies (4) by the proof of the backward direction of Proposition 6.24(2). (7) implies
![]() $(1)_{\mu ^{+\omega }}$
by Proposition 7.5.
$(1)_{\mu ^{+\omega }}$
by Proposition 7.5.
Remark 8.3. In [Reference Grossberg and Vasey18, Corollary 5.5], they did not assume continuity of nonsplitting and showed that: if item (4) in Main Theorem 8.2 holds for
![]() $\mu \geq \beth _\omega (\chi _0+\mu )$
(see Fact 6.3 for the definition of
$\mu \geq \beth _\omega (\chi _0+\mu )$
(see Fact 6.3 for the definition of
![]() $\chi _0$
), then every limit model in
$\chi _0$
), then every limit model in
![]() $K_{\mu ^+}$
is
$K_{\mu ^+}$
is
![]() $\beth _\omega (\chi _0+\mu )$
-saturated. This implies
$\beth _\omega (\chi _0+\mu )$
-saturated. This implies
![]() ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
![]() $\mu ^+$
-nonsplitting. Using [Reference Boney and Vasey12, Theorem 7.1], there is a
$\mu ^+$
-nonsplitting. Using [Reference Boney and Vasey12, Theorem 7.1], there is a
![]() $\lambda <h(\mu ^+)$
such that (3) holds with
$\lambda <h(\mu ^+)$
such that (3) holds with
![]() $\mu $
replaced by
$\mu $
replaced by
![]() $\lambda $
. From hindsight, the last argument can be improved by quoting Corollary 6.11(3) instead and having
$\lambda $
. From hindsight, the last argument can be improved by quoting Corollary 6.11(3) instead and having
![]() $\lambda =\mu ^{++}$
. In comparison, our (4)
$\lambda =\mu ^{++}$
. In comparison, our (4)
![]() $\Rightarrow $
(3) allows (3) to still be in
$\Rightarrow $
(3) allows (3) to still be in
![]() $K_{\mu }$
and does not have the high cardinal threshold.
$K_{\mu }$
and does not have the high cardinal threshold.
Corollary 8.4. Let
![]() $\xi>\operatorname {LS}(\mathbf {K})$
and
$\xi>\operatorname {LS}(\mathbf {K})$
and
![]() $\mathbf {K}$
have a monster model, continuity of
$\mathbf {K}$
have a monster model, continuity of
![]() $\xi $
-nonsplitting and be
$\xi $
-nonsplitting and be
![]() $(<\xi )$
-tame. Then the following are equivalent:
$(<\xi )$
-tame. Then the following are equivalent:
-
1.
 $\mathbf {K}$
has uniqueness of limit models in
$\mathbf {K}$
has uniqueness of limit models in
 $K_\xi $
: for any
$K_\xi $
: for any
 $M_0,M_1,M_2\in K_\xi $
, if both
$M_0,M_1,M_2\in K_\xi $
, if both
 $M_1$
and
$M_1$
and
 $M_2$
are limit over
$M_2$
are limit over
 $M_0$
, then
$M_0$
, then
 $M_1\cong _{M_0}M_2$
.
$M_1\cong _{M_0}M_2$
. -
2.
 $\mathbf {K}$
has uniqueness of limit models without base in
$\mathbf {K}$
has uniqueness of limit models without base in
 $K_\xi $
: any limit models in
$K_\xi $
: any limit models in
 $K_\xi $
are isomorphic.
$K_\xi $
are isomorphic.
Proof The forward direction is immediate and only requires
![]() $JEP$
. For the backward direction, the proof of (3)
$JEP$
. For the backward direction, the proof of (3)
![]() $\Rightarrow $
(1) in Main Theorem 8.2 goes through (
$\Rightarrow $
(1) in Main Theorem 8.2 goes through (
![]() $JEP$
is needed) and we have
$JEP$
is needed) and we have
![]() $\xi $
-superstability. By (1)
$\xi $
-superstability. By (1)
![]() $\Rightarrow $
(3) in Main Theorem 8.2, it has uniqueness of limit models in
$\Rightarrow $
(3) in Main Theorem 8.2, it has uniqueness of limit models in
![]() $K_\xi $
.
$K_\xi $
.
As applications, we present alternative proofs to the results in [Reference Mazari-Armida21, Reference Shelah and Vasey25] with stronger assumptions. In [Reference Mazari-Armida21], limit models of abelian groups are studied.
Fact 8.5.
-
1. [Reference Mazari-Armida21, Definition 3.1 and Fact 3.2] Let
 $\mathbf {K}^{ab}$
be the class of abelian groups ordered by subgroup relation. Then
$\mathbf {K}^{ab}$
be the class of abelian groups ordered by subgroup relation. Then
 $\mathbf {K}^{ab}$
is an AEC with
$\mathbf {K}^{ab}$
is an AEC with
 $\operatorname {LS}(\mathbf {K}^{ab})={\aleph _0}$
, has a monster model and is
$\operatorname {LS}(\mathbf {K}^{ab})={\aleph _0}$
, has a monster model and is
 $(<{\aleph _0})$
-tame.
$(<{\aleph _0})$
-tame. -
2. [Reference Mazari-Armida21, Fact 3.3(2)]
 $\mathbf {K}^{ab}$
is stable in all infinite cardinals.
$\mathbf {K}^{ab}$
is stable in all infinite cardinals. -
3. [Reference Mazari-Armida21, Corollary 3.8]
 $\mathbf {K}^{ab}$
has uniqueness of limit models in all infinite cardinals.
$\mathbf {K}^{ab}$
has uniqueness of limit models in all infinite cardinals.
In the original proof of Fact 8.5(3), an explicit algebraic expression of limit models was obtained, so that limit models of the same cardinality are isomorphic to each other. In [Reference Mazari-Armida21, Remark 3.9], it was remarked that [Reference Vasey38] could be used to obtain uniqueness of limit models for high enough cardinals (above
![]() $\geq \beth _{(2^{{\aleph _0}})^+}$
). We write down the exact argument using known results. Then we present another proof that covers lower cardinals using results in this paper (but not any algebraic description of limit models).
$\geq \beth _{(2^{{\aleph _0}})^+}$
). We write down the exact argument using known results. Then we present another proof that covers lower cardinals using results in this paper (but not any algebraic description of limit models).
First proof of Fact 8.5(3).
In Fact 7.4(1), pick
![]() $\xi \geq (\lambda '(\mathbf {K}))^++\chi _1$
with
$\xi \geq (\lambda '(\mathbf {K}))^++\chi _1$
with
![]() $\operatorname {cf}(\xi )={\aleph _0}$
. By Fact 8.5(2),
$\operatorname {cf}(\xi )={\aleph _0}$
. By Fact 8.5(2),
![]() $\mathbf {K}^{ab}$
is stable in
$\mathbf {K}^{ab}$
is stable in
![]() $\xi $
. So the conclusion of Fact 7.4(1) gives superstability in
$\xi $
. So the conclusion of Fact 7.4(1) gives superstability in
![]() $\geq \lambda '(\mathbf {K}^{ab})$
. By [Reference VanDieren and Vasey31, Corollary 1.4] (which combines [Reference VanDieren and Vasey31, Fact 2.16 and Corollary 6.9]),
$\geq \lambda '(\mathbf {K}^{ab})$
. By [Reference VanDieren and Vasey31, Corollary 1.4] (which combines [Reference VanDieren and Vasey31, Fact 2.16 and Corollary 6.9]),
![]() $\mathbf {K}^{ab}$
has uniqueness of limit models in
$\mathbf {K}^{ab}$
has uniqueness of limit models in
![]() $K^{ab}_{\geq \lambda '(\mathbf {K}^{ab})}$
. Notice that by Fact 7.3,
$K^{ab}_{\geq \lambda '(\mathbf {K}^{ab})}$
. Notice that by Fact 7.3,
![]() $\lambda '( \mathbf {K}^{ab})<h(\lambda (\mathbf {K}^{ab}))=h({\aleph _0})=\beth _{(2^{{\aleph _0}})^+}$
, so we can guarantee uniqueness of limit models above
$\lambda '( \mathbf {K}^{ab})<h(\lambda (\mathbf {K}^{ab}))=h({\aleph _0})=\beth _{(2^{{\aleph _0}})^+}$
, so we can guarantee uniqueness of limit models above
![]() $\beth _{(2^{{\aleph _0}})^+}$
.
$\beth _{(2^{{\aleph _0}})^+}$
.
Second proof of Fact 8.5(3).
By Fact 8.5(1)(2),
![]() $\mathbf {K}^{ab}$
is stable in
$\mathbf {K}^{ab}$
is stable in
![]() ${\aleph _0}$
and is
${\aleph _0}$
and is
![]() $(<{\aleph _0})$
-tame. The latter implies
$(<{\aleph _0})$
-tame. The latter implies
![]() $\omega $
-locality. By Proposition 3.16(2),
$\omega $
-locality. By Proposition 3.16(2),
![]() $\mathbf {K}^{ab}$
has continuity of
$\mathbf {K}^{ab}$
has continuity of
![]() ${\aleph _0}$
-nonsplitting. By Remark 7.7(1), it is superstable in
${\aleph _0}$
-nonsplitting. By Remark 7.7(1), it is superstable in
![]() $\geq {\aleph _0}$
. By Corollary 6.2(1) (or simply [Reference VanDieren and Vasey31, Corollary 1.4]), it has uniqueness of limit models in all infinite cardinals.
$\geq {\aleph _0}$
. By Corollary 6.2(1) (or simply [Reference VanDieren and Vasey31, Corollary 1.4]), it has uniqueness of limit models in all infinite cardinals.
We turn to look at a strictly stable AEC.
Fact 8.6.
-
1. [Reference Mazari-Armida21, Definition 4.1 and Facts 4.2 and 4.5] Let
 $\mathbf {K}^{tf}$
be the class of torsion-free abelian groups ordered by pure subgroup relation. Then
$\mathbf {K}^{tf}$
be the class of torsion-free abelian groups ordered by pure subgroup relation. Then
 $\mathbf {K}^{tf}$
is an AEC with
$\mathbf {K}^{tf}$
is an AEC with
 $\operatorname {LS}(\mathbf {K}^{tf})={\aleph _0}$
, has a monster model and is
$\operatorname {LS}(\mathbf {K}^{tf})={\aleph _0}$
, has a monster model and is
 $(<{\aleph _0})$
-tame.
$(<{\aleph _0})$
-tame. -
2. [Reference Mazari-Armida21, Fact 4.7]
 $\mathbf {K}^{tf}$
is stable in
$\mathbf {K}^{tf}$
is stable in
 $\lambda $
iff
$\lambda $
iff
 $\lambda ^{{\aleph _0}}=\lambda $
. In particular
$\lambda ^{{\aleph _0}}=\lambda $
. In particular
 $\mathbf {K}^{tf}$
is strictly stable.
$\mathbf {K}^{tf}$
is strictly stable. -
3. [Reference Mazari-Armida21, Corollary 4.18] Let
 $\lambda \geq \aleph _1$
.
$\lambda \geq \aleph _1$
.
 $\mathbf {K}^{tf}$
has uniqueness of
$\mathbf {K}^{tf}$
has uniqueness of
 $(\lambda ,\geq \aleph _1)$
-limit models.
$(\lambda ,\geq \aleph _1)$
-limit models. -
4. [Reference Mazari-Armida21, Theorem 4.22] Let
 $\lambda \geq {\aleph _0}$
. Any
$\lambda \geq {\aleph _0}$
. Any
 $(\lambda ,{\aleph _0})$
-limit model in
$(\lambda ,{\aleph _0})$
-limit model in
 $\mathbf {K}^{tf}$
is not algebraically compact.
$\mathbf {K}^{tf}$
is not algebraically compact. -
5. [Reference Mazari-Armida21, Lemmas 4.10 and 4.14] Let
 $\lambda \geq \aleph _1$
. Any
$\lambda \geq \aleph _1$
. Any
 $(\lambda ,\geq \aleph _1)$
-limit model in
$(\lambda ,\geq \aleph _1)$
-limit model in
 $\mathbf {K}^{tf}$
is algebraically compact. Any two algebraically compact limit models in
$\mathbf {K}^{tf}$
is algebraically compact. Any two algebraically compact limit models in
 $K^{tf}_\lambda $
are isomorphic.
$K^{tf}_\lambda $
are isomorphic.
The original proof of the second part of Fact 8.6(3) uses an explicit algebraic expression of algebraically compact groups [Reference Mazari-Armida21, Fact 4.13]. Using the results of this paper, we give a weaker version but without using any algebraic expression of algebraically compact groups.
Proposition 8.7. Assume CH. If
![]() $\mathbf {K}^{tf}$
does not have
$\mathbf {K}^{tf}$
does not have
![]() $\aleph _1$
-order property of length
$\aleph _1$
-order property of length
![]() $\aleph _\omega $
, then for all
$\aleph _\omega $
, then for all
![]() $\lambda \geq \aleph _1$
, it has uniqueness of
$\lambda \geq \aleph _1$
, it has uniqueness of
![]() $(\lambda ,\geq \aleph _1)$
-limit models.
$(\lambda ,\geq \aleph _1)$
-limit models.
Proof By CH and Fact 8.6(2),
![]() $\mathbf {K}^{tf}$
is stable in
$\mathbf {K}^{tf}$
is stable in
![]() $\aleph _1$
. By Fact 8.6(1),
$\aleph _1$
. By Fact 8.6(1),
![]() $\mathbf {K}^{tf}$
is
$\mathbf {K}^{tf}$
is
![]() $(<{\aleph _0})$
-tame, hence it has
$(<{\aleph _0})$
-tame, hence it has
![]() $\omega $
-locality. By Proposition 3.16(2),
$\omega $
-locality. By Proposition 3.16(2),
![]() $\mathbf {K}^{tf}$
has continuity of
$\mathbf {K}^{tf}$
has continuity of
![]() $\lambda $
-nonsplitting for all
$\lambda $
-nonsplitting for all
![]() $\lambda \geq \aleph _1$
. Proposition 3.9 and Lemma 6.7 give
$\lambda \geq \aleph _1$
. Proposition 3.9 and Lemma 6.7 give
![]() $\aleph _1$
-local character of
$\aleph _1$
-local character of
![]() $\lambda $
-nonsplitting for all
$\lambda $
-nonsplitting for all
![]() $\lambda \geq \aleph _1$
. By Fact 6.10(1),
$\lambda \geq \aleph _1$
. By Fact 6.10(1),
![]() $\mathbf {K}^{tf}$
is stable in
$\mathbf {K}^{tf}$
is stable in
![]() $[\aleph _1,\aleph _\omega )$
. By Corollary 6.2(1) and Remark 6.8(1),
$[\aleph _1,\aleph _\omega )$
. By Corollary 6.2(1) and Remark 6.8(1),
![]() $\mathbf {K}^{tf}$
has uniqueness of
$\mathbf {K}^{tf}$
has uniqueness of
![]() $(\lambda ,\geq \aleph _1)$
-limit models for all
$(\lambda ,\geq \aleph _1)$
-limit models for all
![]() $\lambda \geq \aleph _1$
.
$\lambda \geq \aleph _1$
.
Question 8.8. Is it true that
![]() $\mathbf {K}^{tf}$
does not have
$\mathbf {K}^{tf}$
does not have
![]() $\aleph _1$
-order property of length
$\aleph _1$
-order property of length
![]() $\aleph _\omega $
?
$\aleph _\omega $
?
For Fact 8.6(4), the original proof argued that uniqueness of limit models eventually leads to superstability for large enough
![]() $\lambda $
(from an older result in [Reference Grossberg and Vasey18]). Then a specific construction deals with small
$\lambda $
(from an older result in [Reference Grossberg and Vasey18]). Then a specific construction deals with small
![]() $\lambda $
. In [Reference Mazari-Armida21, Remark 4.23], it was noted that [Reference Vasey38, Lemma 4.12] could deal with both cases of
$\lambda $
. In [Reference Mazari-Armida21, Remark 4.23], it was noted that [Reference Vasey38, Lemma 4.12] could deal with both cases of
![]() $\lambda $
. We give a full proof here (the algebraic description of limit models is needed):
$\lambda $
. We give a full proof here (the algebraic description of limit models is needed):
Proof of Fact 8.6(4)
Let
![]() $\lambda \geq {\aleph _0}$
and M be a
$\lambda \geq {\aleph _0}$
and M be a
![]() $(\lambda ,{\aleph _0})$
-limit model. Then
$(\lambda ,{\aleph _0})$
-limit model. Then
![]() $\mathbf {K}^{tf}$
is stable in
$\mathbf {K}^{tf}$
is stable in
![]() $\lambda $
and by Fact 8.6(2)
$\lambda $
and by Fact 8.6(2)
![]() $\lambda>{\aleph _0}$
. Suppose M is algebraically compact, by Fact 8.6(5) and Corollary 6.2(2) M is isomorphic to
$\lambda>{\aleph _0}$
. Suppose M is algebraically compact, by Fact 8.6(5) and Corollary 6.2(2) M is isomorphic to
![]() $(\lambda ,\geq \aleph _1)$
-limit models and is saturated. By Proposition 6.12(3) (where
$(\lambda ,\geq \aleph _1)$
-limit models and is saturated. By Proposition 6.12(3) (where
![]() $\langle M_i:i\leq {\aleph _0}\rangle $
witnesses that M is
$\langle M_i:i\leq {\aleph _0}\rangle $
witnesses that M is
![]() $(\lambda ,{\aleph _0})$
-limit),
$(\lambda ,{\aleph _0})$
-limit),
![]() ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
![]() $\lambda $
-nonsplitting applies to M. Since M is arbitrary,
$\lambda $
-nonsplitting applies to M. Since M is arbitrary,
![]() $\mathbf {K}^{tf}$
has
$\mathbf {K}^{tf}$
has
![]() ${\aleph _0}$
-local character of
${\aleph _0}$
-local character of
![]() $\lambda $
-nonsplitting, which implies stability in
$\lambda $
-nonsplitting, which implies stability in
![]() $\geq \lambda $
by Fact 6.10(2), contradicting Fact 8.6(2).
$\geq \lambda $
by Fact 6.10(2), contradicting Fact 8.6(2).
Remark 8.9. [Reference Vasey38, Lemma 4.12] happened to work because we do not care about the case
![]() ${\aleph _0}$
(which is not stable) and we can always apply item (3) in Proposition 6.12.
${\aleph _0}$
(which is not stable) and we can always apply item (3) in Proposition 6.12.
In [Reference Shelah and Vasey25],
![]() $\aleph _0$
-stable AECs with
$\aleph _0$
-stable AECs with
![]() ${\aleph _0}$
-
${\aleph _0}$
-
![]() $AP$
,
$AP$
,
![]() ${\aleph _0}$
-
${\aleph _0}$
-
![]() $JEP,$
and
$JEP,$
and
![]() ${\aleph _0}$
-
${\aleph _0}$
-
![]() $NMM$
were studied. They built a superlimit model in
$NMM$
were studied. They built a superlimit model in
![]() ${\aleph _0}$
by connecting limit models with sequentially homogeneous models [Reference Shelah and Vasey25, Theorem 4.4]. Then they defined splitting over finite sets where types have countable domains and obtained finite character assuming categoricity in
${\aleph _0}$
by connecting limit models with sequentially homogeneous models [Reference Shelah and Vasey25, Theorem 4.4]. Then they defined splitting over finite sets where types have countable domains and obtained finite character assuming categoricity in
![]() ${\aleph _0}$
[Reference Shelah and Vasey25, Fact 5.3]. This allowed them to build a good
${\aleph _0}$
[Reference Shelah and Vasey25, Fact 5.3]. This allowed them to build a good
![]() ${\aleph _0}$
-frame over models generated by the superlimit. These methods are absent in our paper because we studied AECs with a general
${\aleph _0}$
-frame over models generated by the superlimit. These methods are absent in our paper because we studied AECs with a general
![]() $\operatorname {LS}(\mathbf {K})$
, and our splitting is defined for types of model-domains.
$\operatorname {LS}(\mathbf {K})$
, and our splitting is defined for types of model-domains.
In [Reference Shelah and Vasey25, Corollary 5.9], they showed the existence of a superlimit in
![]() $\aleph _1$
assuming weak
$\aleph _1$
assuming weak
![]() $(<{\aleph _0},{\aleph _0})$
-locality among other assumptions. We will strengthen the locality assumption to
$(<{\aleph _0},{\aleph _0})$
-locality among other assumptions. We will strengthen the locality assumption to
![]() $\omega $
-locality, and work in a monster model to give an alternative proof. This allows us to bypass the machineries in [Reference Shelah and Vasey25] that are sensitive to the cardinal
$\omega $
-locality, and work in a monster model to give an alternative proof. This allows us to bypass the machineries in [Reference Shelah and Vasey25] that are sensitive to the cardinal
![]() ${\aleph _0}$
, and the technical manipulation of symmetry in [Reference Shelah and Vasey25, Section 3]. Also, our result extends to a general
${\aleph _0}$
, and the technical manipulation of symmetry in [Reference Shelah and Vasey25, Section 3]. Also, our result extends to a general
![]() $\operatorname {LS}(\mathbf {K})$
.
$\operatorname {LS}(\mathbf {K})$
.
Proposition 8.10. Let
![]() $\mathbf {K}$
is an
$\mathbf {K}$
is an
![]() ${\aleph _0}$
-stable AEC with a monster model and has
${\aleph _0}$
-stable AEC with a monster model and has
![]() $\omega $
-locality. Then there is a superlimit in
$\omega $
-locality. Then there is a superlimit in
![]() $\aleph _1$
. In general, let
$\aleph _1$
. In general, let
![]() $\lambda \geq \operatorname {LS}(\mathbf {K})$
, and if
$\lambda \geq \operatorname {LS}(\mathbf {K})$
, and if
![]() $\mathbf {K}$
is stable in
$\mathbf {K}$
is stable in
![]() $\lambda $
instead of
$\lambda $
instead of
![]() ${\aleph _0}$
, then it has a superlimit in
${\aleph _0}$
, then it has a superlimit in
![]() $\lambda ^+$
.
$\lambda ^+$
.
Proof Apply Main Theorem 8.2(1)
![]() $\Rightarrow $
(5) where
$\Rightarrow $
(5) where
![]() $\mu =\operatorname {LS}(\mathbf {K})$
(that direction does not require
$\mu =\operatorname {LS}(\mathbf {K})$
(that direction does not require
![]() $\mu>\operatorname {LS}(\mathbf {K})$
). Notice that
$\mu>\operatorname {LS}(\mathbf {K})$
). Notice that
![]() $\omega $
-locality implies
$\omega $
-locality implies
![]() $\operatorname {LS}(\mathbf {K})$
-tameness.
$\operatorname {LS}(\mathbf {K})$
-tameness.
Tracing our proof, we require global assumptions of a monster model and
![]() $\omega $
-locality in order to use our symmetry results, especially Proposition 5.9. We end this section with the following:
$\omega $
-locality in order to use our symmetry results, especially Proposition 5.9. We end this section with the following:
Question 8.11. Instead of global assumptions like monster model and no-order-property, is it possible to obtain local symmetry properties in Section 5 using more local assumptions?
Acknowledgments
This paper was written while the author was working on a Ph.D. under the direction of Rami Grossberg at Carnegie Mellon University and we would like to thank Prof. Grossberg for his guidance and assistance in my research in general and in this work in particular.