Article contents
A stochastic interpretation of propositional dynamic logic: expressivity
Published online by Cambridge University Press: 12 March 2014
Abstract
We propose a probabilistic interpretation of Propositional Dynamic Logic (PDL). We show that logical and behavioral equivalence are equivalent over general measurable spaces. This is done first for the fragment of straight line programs and then extended to cater for the nondeterministic nature of choice and iteration, expanded to PDL as a whole. Bisimilarity is also discussed and shown to be equivalent to logical and behavioral equivalence, provided the base spaces are Polish spaces. We adapt techniques from coalgebraic stochastic logic and point out some connections to Souslin's operation 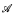 from descriptive set theory. This leads to a discussion of complete stochastic Kripke models and model completion, which permits an adequate treatment of the test operator.
from descriptive set theory. This leads to a discussion of complete stochastic Kripke models and model completion, which permits an adequate treatment of the test operator.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012
References
REFERENCES
- 9
- Cited by

