No CrossRef data available.
Article contents
Strong 0-1 laws in finite model theory
Published online by Cambridge University Press: 12 March 2014
Abstract
We introduce a new framework for asymptotic probabilities of sentences, in which we have a σ-additive measure on the sample space of all sequences A = {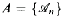 } of finite models, where the universe of
} of finite models, where the universe of 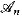 is {1,2, …, n}. and use this framework to strengthen 0-1 laws for logics.
is {1,2, …, n}. and use this framework to strengthen 0-1 laws for logics.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
[1]Compton, K. J., 0-1 laws in logic and combinatorics, NATO advanced study institute on algorithms and order, 1987, pp. 353–383.Google Scholar
[2]Compton, K. J., A logical approach to asymptotic combinatorics I: first order properties. Advances in Mathematics, vol. 65 (1987), pp. 65–96.CrossRefGoogle Scholar
[3]Compton, K. J., The computational complexity of asymptotic problems I: partial orders, Information and Computation, vol. 78 (1988), pp. 108–123.CrossRefGoogle Scholar
[4]Compton, K. J., A logical approach to asymptotic combinatorics II: monadic second-order properties, Journal of Combinatorial Theory, Series A, vol. 50 (1989), pp. 110–131.CrossRefGoogle Scholar
[5]Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), pp. 17–21.Google Scholar
[6]Glebskii, Y. V., Kogan, D. I., Liogonki, M. I., and Talanov, V. A., Range and degree of realizability of formulas in the restricted predicate calculus, Cybernetics, vol. 5 (1969), pp. 142–154.CrossRefGoogle Scholar
[8]Hayman, W. K., A generalisation of Stirling's formula, Journal fuer angewandte undreine Mathematik, vol. 196 (1956), pp. 67–95.CrossRefGoogle Scholar
[9]Hella, L., Kolaitis, P. G., and Luosto, K., Almost everywhere equivalence of logics infinite model theory, The Bulletin of Symbolic Logic, vol. 2 (December 1996), no. 4, pp. 422–443.CrossRefGoogle Scholar
[10]Kleitman, D. J. and Rothschild, B. L., Asymptotic enumeration of partial orders on a finite set, Transactions of the American Mathematical Society, vol. 205 (1975), pp. 205–220.CrossRefGoogle Scholar
[11]Kolaitis, P. G. and Vardi, M. Y., Infinitary logics and 0-1 laws, Information and Computation, vol. 98 (1992), pp. 258–294, special issue: selections from the fifth annual IEEE symposium on logic in computer science.CrossRefGoogle Scholar
[12]Luczak, T. and Spencer, J., When does the zero-one law hold, Journal of the American Mathematical Society, vol. 4 (3) (1991), pp. 451–468.CrossRefGoogle Scholar
[13]Lynch, J. F.. Almost sure theories, Annals of Mathematical Logic, vol. 18 (1980), pp. 91–135.CrossRefGoogle Scholar
[14]Mycielski, J., Measure and category of some sets of models, Notices of the American Mathematical Society, vol. 22 (1975), pp. A–475.Google Scholar
[15]Oxtoby, J. C., Measure and category: A survey of the analogies between topological and measure spaces, 2n ded., Springer-Verlag, New York–Heidelberg–Berlin, 1980.CrossRefGoogle Scholar
[16]Shelah, S. and Spencer, J., Zero-one laws for sparse random graphs, Journal of the American Mathematical Society, vol. 1 (1988), pp. 97–115.CrossRefGoogle Scholar
[17]Williams, D., Probability with martingales, Cambridge University Press, 1991.CrossRefGoogle Scholar
[18]Problems infinite model theory, collected during the conference on Finite Model theory in Luminy, 1995, http://www.informatik.rwth-aachen.de/www-math/fmt.html.Google Scholar

