Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T17:08:41.244Z Has data issue: false hasContentIssue false
  • English
  • Français

The strong anticupping property for recursively enumerable degrees1

Published online by Cambridge University Press:  12 March 2014

S. B. Cooper
S. B. Cooper*
Affiliation:
Department of Mathematics, University of Leeds, Leeds LS2 9JT, England
Get access Rights & Permissions [Opens in a new window]

Extract

Following Soare [11] we say a recursively enumerable (r.e.) degree a has the anticupping (a.c.) property if there is a nonzero r.e. degree b < a such that for no r.e. c < a does a = b ∪ c.

Cooper [2] and Yates showed that 0′ has the a.c. property, while Harrington (see Miller [6]) proved that every high r.e. degree a has the a.c. property.

The recent paper by Ambos-Spies, Jockusch, Shore and Soare [1] describes a general theoretical framework for cupping and capping below 0′ which seems likely to be useful in a wider context.

Definition. (1) We say b is strongly noncuppable belowa if 0 < b < a and, for each d < a, b ∪ d ≠ a.

(2) We say an r.e. a has the strong anticupping property if there is an r.e. b which is strongly noncuppable below a.

The main results on cupping in 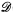(≤ 0′) are due to Epstein, Posner and Robinson. For instance it is known (Posner and Robinson [8]) that the s.a.c. property fails for 0′.

We prove below that r.e. degrees with the s.a.c. property do exist, hence obtaining a nonzero r.e. degree a such that 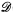(≤ a) ≢e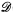(≤h) for any high r.e. degree h. This result, obtained by means of an infinite injury construction in 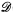(≤ 0′), extends Theorem 2 of [3], proved using a finite injury construction in 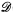(≤ 0′).

Our main source of notation and terminology is [3].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 2 , June 1989 , pp. 527 - 539
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

We are grateful to the referee for a number of helpful suggestions and corrections. We are also grateful for valuable help from C. G. Jockusch and R. I. Soare in the preparation of the paper.

References

REFERENCE

[1]Ambos-Spies, K.et al., An algebraic decomposition of the recursively enumerable degrees and the coincidence of several degree classes with the promptly simple degrees, Transactions of the American Mathematical Society, vol. 281 (1984), pp. 109–128.CrossRefGoogle Scholar
[2]Cooper, S. B., On a theorem of C. E. M. Yates, handwritten notes, 1974.Google Scholar
[3]Cooper, S. B. and Epstein, R. L., Complementing below recursively enumerable degrees, Annals of Pure and Applied Logic, vol. 34 (1987), pp. 15–32.CrossRefGoogle Scholar
[4]Epstein, R. L., Initial segments of the degrees below 0′, Memoir no. 241, American Mathematical Society, Providence, Rhode Island, 1981.CrossRefGoogle Scholar
[5]Lachlan, A. H., Lower bounds for pairs of r.e. degrees, Proceedings of the London Mathematical Society, ser. 3, vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[6]Miller, D., High recursively enumerable degrees and the anticupping property, Logic year 1979–80 (Lerman, M.et al., editors), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 230–267.CrossRefGoogle Scholar
[7]Posner, D. B., High degrees, Ph.D. thesis, University of California, Berkeley, California, 1977.Google Scholar
[8]Posner, D. and Robinson, R. W., Degrees joining to 0′, this Journal, vol. 46 (1981), pp. 714–721.Google Scholar
[9]Sacks, G. E., Degrees of unsoltability, Annals of Mathematics Studies, vol. 55, Princeton University Press, Princeton, New Jersey, 1963.Google Scholar
[10]Shore, R. A., The theory of the degrees below 0′, Journal of the London Mathematical Society, ser. 2, vol. 24 (1981), pp. 1–14.CrossRefGoogle Scholar
[11]Soare, R. I., Tree arguments in recursion theory and the 0′″-priority method, Recursion theory (Nerode, A. and Shore, R. A., editors), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, Rhode Island, 1985, pp. 53–106.CrossRefGoogle Scholar