No CrossRef data available.
Article contents
Strong convergence in finite model theory
Published online by Cambridge University Press: 12 March 2014
Abstract
In [9] we introduced a new framework for asymptotic probabilities, in which a σ-additive measure is defined on the sample space of all sequences 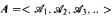 of finite models, where the universe of
of finite models, where the universe of 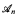 , is {1,2,…,n}. In this framework we investigated the strong 0-1 law for sentences, which states that each sentence either holds in
, is {1,2,…,n}. In this framework we investigated the strong 0-1 law for sentences, which states that each sentence either holds in 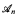 eventually almost surely or fails in
eventually almost surely or fails in 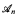 eventually almost surely.
eventually almost surely.
In this paper we define the strong convergence law for formulas, which carries over the ideas of the strong 0-1 law to formulas with free variables, and roughly states that for each formula ϕ(x), the fraction of tuples a in 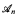 , which satisfy the formula ϕ(x), almost surely has a limit as n tends to infinity.
, which satisfy the formula ϕ(x), almost surely has a limit as n tends to infinity.
We show that the infinitary logic with finitely many variables has the strong convergence law for formulas for the uniform measure, and further characterize the measures on random graphs for which the strong convergence law holds.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002

