No CrossRef data available.
Article contents
THE STRUCTURAL COMPLEXITY OF MODELS OF ARITHMETIC
Published online by Cambridge University Press: 29 June 2023
Abstract
We calculate the possible Scott ranks of countable models of Peano arithmetic. We show that no non-standard model can have Scott rank less than 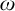 $\omega $ and that non-standard models of true arithmetic must have Scott rank greater than
$\omega $ and that non-standard models of true arithmetic must have Scott rank greater than 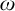 $\omega $. Other than that there are no restrictions. By giving a reduction via
$\omega $. Other than that there are no restrictions. By giving a reduction via 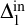 $\Delta ^{\mathrm {in}}_{1}$ bi-interpretability from the class of linear orderings to the canonical structural
$\Delta ^{\mathrm {in}}_{1}$ bi-interpretability from the class of linear orderings to the canonical structural 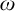 $\omega $-jump of models of an arbitrary completion T of
$\omega $-jump of models of an arbitrary completion T of 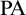 $\mathrm {PA}$ we show that every countable ordinal
$\mathrm {PA}$ we show that every countable ordinal  $\alpha>\omega $ is realized as the Scott rank of a model of T.
$\alpha>\omega $ is realized as the Scott rank of a model of T.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
Alvir, R., Greenberg, N., Harrison-Trainor, M., and Turetsky, D., Scott complexity of countable structures, this Journal, vol. 86 (2021), no. 4, pp. 1706–1720.Google Scholar
Alvir, R. and Rossegger, D., The complexity of Scott sentences of scattered linear orders, this Journal, vol. 85 (2020), no. 3, pp. 1079–1101.Google Scholar
Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, Elsevier, Amsterdam, 2000.Google Scholar
Ash, C., Knight, J., Manasse, M., and Slaman, T., Generic copies of countable structures
. Annals of Pure and Applied Logic, vol. 42 (1989), no. 3, pp. 195–205.CrossRefGoogle Scholar
Ash, C. J., Recursive labelling systems and stability of recursive structures in hyperarithmetical degrees
. Transactions of the American Mathematical Society, vol. 298 (1986), no. 2, pp. 497–514.CrossRefGoogle Scholar
Barwise, J., Back and forth through infinitary logic
. Studies in Model Theory, vol. 8 (1973), pp. 5–34.Google Scholar
Chisholm, J., Effective model theory vs. recursive model theory, this Journal, vol. 55 (1990), no. 3, pp. 1168–1191.Google Scholar
Coskey, S. and Kossak, R., The complexity of classification problems for models of arithmetic
. Bulletin of Symbolic Logic, vol. 16 (2010), no. 3, pp. 345–358.CrossRefGoogle Scholar
Gaifman, H., Models and types of Peano’s arithmetic
. Annals of Mathematical Logic, vol. 9 (1976), no. 3, pp. 223–306.CrossRefGoogle Scholar
Gonzalez, D. and Rossegger, D., Scott sentence complexities of linear orderings, submitted, 2023, arXiv:2305.07126.CrossRefGoogle Scholar
Harrison-Trainor, M., Miller, R., and Montalbán, A., Borel functors and infinitary interpretations, this Journal, vol. 83 (2018), no. 4, pp. 1434–1456.Google Scholar
Karp, C. R., Finite-quantifier equivalence
, The Theory of Models, Proceedings of the 1963 International Symposium at Berkeley, North-Holland, Amsterdam, 1965, pp. 407–412.Google Scholar
Kossak, R. and Schmerl, J., The Structure of Models of Peano Arithmetic, Oxford Logic Guides, vol. 50, Oxford University Press, Oxford, 2006.CrossRefGoogle Scholar
Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas. Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.Google Scholar
Makkai, M., An example concerning Scott heights, this Journal, vol. 46 (1981), no. 2, pp. 301–318.Google Scholar
Montalbán, A., Notes on the jump of a structure
, Mathematical Theory and Computational Practice (K. Ambos-Spies, B. Löwe, and W. Merkle, editors), Springer, Berlin, 2009, pp. 372–378.CrossRefGoogle Scholar
Montalbán, A., A robuster Scott rank
. Proceedings of the American Mathematical Society, vol. 143 (2015), no. 12, pp. 5427–5436.CrossRefGoogle Scholar
Montalbán, A., Computable Structure Theory: Within the Arithmetic, Cambridge University Press, Cambridge, 2021.CrossRefGoogle Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers
, The Theory of Models (J. W. Addison, L. Henkin, and A. Tarski, editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, vol. 1
, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Vaught, R., Invariant sets in topology and logic
. Fundamenta Mathematicae, vol. 82 (1974), pp. 269–294.CrossRefGoogle Scholar


