Structures elementarily closed relative to a model for arithmetic

Extract

The present paper is a sequel to [1]. It is our purpose to formulate a general theory derived from the methods used to obtain three results for the field of real algebraic numbers in [1]. As there, we shall concern ourselves almost exclusively with fields of characteristic zero; thus we assume a convenient formulation of first order logic with extralogical constants E(x, y), S(x, y, z), F(x, y, z), F(x, y), N(x) and 0, whose intended interpretations are equality, sum, product, y is the successor of x, x ∈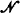 (where 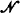is a substructure satisfying all first order truths of the natural numbers) and zero, respectively. In addition, we shall use Q(x, y) for x ≤ y in those cases where our field is ordered, e.g. the field of real algebraic numbers.