Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T18:18:55.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Tense logic for discrete future time

Published online by Cambridge University Press:  12 March 2014

Patrick Schindler
Patrick Schindler*
Affiliation:
Balliol College, Oxford
Get access Rights & Permissions [Opens in a new window]

Extract

Prior has conjectured that the tense-logical system Gli obtained by adding to a complete basis for the classical propositional calculus the primitive symbol G, the definitions

Df. F: Fα = NGNα

Df. L: Lα = KαGα,

and the postulates

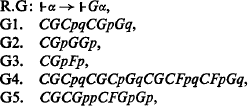
is complete for the logic of linear, infinite, transitive, discrete future time. In this paper it is demonstrated that that conjecture is correct and it is shown that Gli has the finite model property: see [4]. The techniques used are in part suggested by those used in Bull [2] and [3]:

Gli can be shown to be complete for the logic of linear, infinite, transitive, discrete future time in the sense that every formula of Gli which is true of such time can be proved as a theorem of Gli. For this purpose the notion of truth needs to be formalized. This formalization is effected by the construction of a model for linear, infinite, transitive, discrete future time.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 35 , Issue 1 , March 1970 , pp. 105 - 118
Copyright
Copyright © Association for Symbolic Logic 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Garrett, Birkhoff, Subdirect unions in universal algebra, Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 764–768.Google Scholar
[2] Bull, R. A., An algebraic study of Diodorean modal systems, this Journal, vol. 30 (1965), pp. 58–64.Google Scholar
[3] Bull, R. A., An algebraic study of tense logics with linear time, this Journal, vol. 33 (1968), pp. 27–38.Google Scholar
[4] Harrop, R., On the existence of finite models and decision procedures for prepositional calculi, Proceedings of the Cambridge Philosophical Society, vol. 54 (1958), pp. 1–13.CrossRefGoogle Scholar
[5] Kurosh, A. G., Lectures on general algebra, Chelsea, New York, 1963.Google Scholar
[6] Lemmon, E. J., Algebraic semantics for modal logics. I, this Journal, vol. 31 (1966), pp. 46–65.Google Scholar
[7] McKinsey, J. C. C., A solution of the decision problem for the Lewis systems S2 and S4 with an application to topology, this Journal, vol. 6 (1941), pp. 117–134.Google Scholar
[8] McKinsey, J. C. C. and Tarski, Alfred, The algebra of topology, Annals of mathematics, vol. 45 (1944), pp. 141–191.CrossRefGoogle Scholar
[9] Prior, A. N., Past, present and future, Clarendon, Oxford, 1967.CrossRefGoogle Scholar