Article contents
Theories with recursive models
Published online by Cambridge University Press: 12 March 2014
Extract
A structure 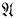 is recursive if the set of quantifier-free sentences in the complete diagram ⊿(
is recursive if the set of quantifier-free sentences in the complete diagram ⊿(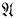 ) of
) of 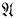 is recursive. It has been known for some time that every decidable theory has a recursive model. In fact, every decidable theory has a decidable model
is recursive. It has been known for some time that every decidable theory has a recursive model. In fact, every decidable theory has a decidable model 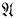 (that is a model
(that is a model 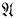 such that ⊿(
such that ⊿(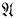 ) is recursive). In this paper we find other conditions which imply that a theory have a recursive model.
) is recursive). In this paper we find other conditions which imply that a theory have a recursive model.
In §1 we study the relation between an ℵ0-categorical theory T having a recursive model and the complexity of the quantificational hierarchy of that theory. We let ∃0 denote the set of quantifier-free sentences, and let ∃n÷1 denote the set of sentences beginning with an existential quantifier and having n alternations of quantifiers. (∀n is defined analogously.) Then we show that if T is an arithmetical ℵ0-categorical theory such that T ⋂ ∃n÷2 is Σn÷10 for each n < ω, then T has a recursive model. We show that this is a best possible result by giving an example of a ⊿n÷20 ℵ0-categorical theory T such that T ⋂ ∃n÷1 is recursive yet T has no recursive model.
In §2 we consider the theory of trees. Ershov [1] had proved that every Σ10 theory of trees has a recursive model. We show this to be best possible by giving an example of a ⊿20 theory of trees which has no recursive model.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1979
References
REFERENCES
- 20
- Cited by

