Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Takeuti, Gaisi
1962.
On the weak definability in set theory.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 38,
Issue. 2,
1963.
Introduction to Model Theory and to the Metamathematics of Algebra.
Vol. 32,
Issue. ,
p.
272.
Keisler, H. Jerome
1964.
Unions of relational systems.
Proceedings of the American Mathematical Society,
Vol. 15,
Issue. 4,
p.
540.
Keisler, H. Jerome
1965.
Reduced products and Horn classes.
Transactions of the American Mathematical Society,
Vol. 117,
Issue. 0,
p.
307.
LINDSTRÖM, PER
1966.
On Relations between Structures.
Theoria,
Vol. 32,
Issue. 3,
p.
172.
Mustafin, T. G.
1968.
(n,l)-sums of models.
Soviet Mathematical Journal,
Vol. 9,
Issue. 1,
p.
87.
Yeh, Raymond T.
1968.
On relational homomorphisms of automata.
Information and Control,
Vol. 13,
Issue. 2,
p.
140.
Feferman, Solomon
1968.
Proceedings of the Summer School in Logic Leeds, 1967.
Vol. 70,
Issue. ,
p.
1.
Fittler, R.
1969.
Category Theory, Homology Theory and their Applications I.
Vol. 86,
Issue. ,
p.
33.
Galvin, Fred
1970.
Horn sentences.
Annals of Mathematical Logic,
Vol. 1,
Issue. 4,
p.
389.
1971.
The Metamathematics of Algebraic Systems - Collected Papers: 1936–1967.
Vol. 66,
Issue. ,
p.
474.
Krauss, Peter
1971.
Universally Complete Universal Theories.
Mathematical Logic Quarterly,
Vol. 17,
Issue. 1,
p.
351.
Richter, Michael
1971.
Limites in Kategorien von Relationalsystemen.
Mathematical Logic Quarterly,
Vol. 17,
Issue. 1,
p.
75.
Fittler, Robert
1972.
A Characteristic Direct Limit Property.
Mathematical Logic Quarterly,
Vol. 18,
Issue. 8-11,
p.
131.
MOTOHASHI, Nobuyoshi
1972.
Interpolation Theorem and Characterization Theorem.
Annals of the Japan Association for Philosophy of Science,
Vol. 4,
Issue. 2,
p.
85.
Fujiwara, T.
1973.
A generalization of Lyndon’s theorem characterizing sentences preserved in subdirect products.
Algebra Universalis,
Vol. 3,
Issue. 1,
p.
280.
Isbell, John R.
1973.
Functorial implicit operations.
Israel Journal of Mathematics,
Vol. 15,
Issue. 2,
p.
185.
Fujiwara, Tsuyoshi
1973.
Note on generalized atomic sets of formulas.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 49,
Issue. 6,
Fittler, Robert
1974.
Saturated models of incomplete theories.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 16,
Issue. 1-2,
p.
3.
Armbrust, Manfred
and
Kaiser, Klaus
1974.
On some properties a projective model class passes on to the generated axiomatic class.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 16,
Issue. 3-4,
p.
133.

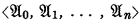 of relational systems is said to be a
of relational systems is said to be a 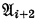 is an elementary extension of
is an elementary extension of 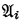 (
(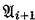 is an extension of
is an extension of  (
(