Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-31T21:28:18.041Z Has data issue: false hasContentIssue false
  • English
  • Français

A THEORY OF PAIRS FOR NON-VALUATIONAL STRUCTURES

Published online by Cambridge University Press:  25 January 2019

ELITZUR BAR-YEHUDA ,
ASSAF HASSON  and
YA’ACOV PETERZIL
ELITZUR BAR-YEHUDA
Affiliation:
DEPARTMENT OF MATHEMATICS BEN GURION UNIVERSITY OF THE NEGEV BE’ER SEHVA, ISRAELE-mail: elitzur.by@gmail.com
ASSAF HASSON
Affiliation:
DEPARTMENT OF MATHEMATICS BEN GURION UNIVERSITY OF THE NEGEV BE’ER SEHVA, ISRAELE-mail: hassonas@math.bgu.ac.ilURL: http://www.math.bgu.ac.il/∼hasson/
YA’ACOV PETERZIL
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF HAIFA HAIFA, ISRAELE-mail: kobi@math.haifa.ac.ilURL: http://math.haifa.ac.il/kobi/
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a weakly o-minimal structure 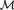${\cal M}$ and its o-minimal completion 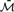$\bar{{\cal M}}$, we first associate to 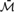$\bar{{\cal M}}$ a canonical language and then prove that Th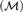$\left( {\cal M} \right)$ determines 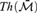$Th\left( {\bar{{\cal M}}} \right)$. We then investigate the theory of the pair 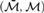$\left( {\bar{{\cal M}},{\cal M}} \right)$ in the spirit of the theory of dense pairs of o-minimal structures, and prove, among other results, that it is near model complete, and every definable open subset of 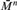${\bar{M}^n}$ is already definable in 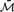$\bar{{\cal M}}$.

We give an example of a weakly o-minimal structure interpreting 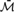$\bar{{\cal M}}$ and show that it is not elementarily equivalent to any reduct of an o-minimal trace.

Keywords

03C64weakly o-minimal structuresnon-valuationaldense pairso-minimal traces

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 2 , June 2019 , pp. 664 - 683
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Baisalov, Y. and Poizat, B., Paires de structures o-minimales, this Journal, vol. 63 (1998), no. 2, pp. 570–578.Google Scholar
Boxall, G. and Hieronymi, P., Expansions which introduce no new open sets, this Journal, vol. 77 (2012), no. 1, pp. 111–121.Google Scholar
Eleftheriou, A., Gunaydin, P. E., and Hieronymi, P., Structure theorems in tame expansions of o-minimal structures by a dense set, arXiv e-prints, 2017.Google Scholar
Eleftheriou, P. E., Hasson, A., and Keren, G., On definable Skolem functions in weakly o-minimal non-valuational structures, this Journal, vol. 82 (2017), no. 4, 1482–1495.Google Scholar
Keren, G., Definable compactness in weakly o-minimal structures, Master’s thesis, Ben Gurion University of the Negev, 2014.Google Scholar
Macpherson, D., Marker, D., and Steinhorn, C., Weakly o-minimal structures and real closed fields. Transactions of the American Mathematical Society, vol. 352 (2000), no. 12, pp. 5435–5483. (electronic).10.1090/S0002-9947-00-02633-7CrossRefGoogle Scholar
Marker, D., Model Theory: An Introduction, Graduate Texts in Mathematics, vol. 217, Springer-Verlag, New York, 2002.Google Scholar
Miller, C. and Starchenko, S., A growth dichotomy for o-minimal expansions of ordered groups. Transactions of the American Mathematical Society, vol. 350 (1998), no. 9, pp. 3505–3521.10.1090/S0002-9947-98-02288-0CrossRefGoogle Scholar
van den Dries, L., Dense pairs of o-minimal structures. Fundamenta Mathematicae, vol. 157 (1998), no. 1, pp. 61–78.Google Scholar
Wencel, R., Weakly o-minimal nonvaluational structures. Annals of Pure and Applied Logic, vol. 154 (2008), no. 3, pp. 139–162.10.1016/j.apal.2008.01.009CrossRefGoogle Scholar
Wencel, R., On the strong cell decomposition property for weakly o-minimal structures. Mathematical Logic Quarterly, vol. 59 (2013), no. 6, pp. 452–470.10.1002/malq.201200016CrossRefGoogle Scholar