Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T19:32:22.303Z Has data issue: false hasContentIssue false
  • English
  • Français

A theory of restricted quantification I

Published online by Cambridge University Press:  12 March 2014

Theodore Hailperin
Theodore Hailperin*
Affiliation:
Lehigh University
Get access Rights & Permissions [Opens in a new window]

Extract

The notion of a variable restricted in range to some set of values, or to values having some property, is widespread in logic and mathematics. To avoid continual explicit mention of such a restriction the common device is to resort to a typographically different set of letters for such variables. But a notation of this kind is clearly inadequate when a general discussion, including more than one kind of restriction, is under consideration. For example, two restrictions may have some inner connection, as in the case of mutually exclusive restrictions, and this the usual symbolism doesn't depict; or, one may wish to study the dependence of such restrictions upon one or more parameters as in the case of bounded quantifiers of recursive function theory; or, one can even conceive of restrictions which may in turn depend upon restricted variables. In each of these cases the currently used notation is deficient.

If x is an individual-variable and Q a formula of the predicate calculus, then for the idea ‘x such that Q’ the notation ‘vxQ’ is proposed as one having the requisite degree of notational multiplicity – the ‘vx’ acting as a binding operator for free occurrences of x in Q. The expression ‘vxQ’ is referred to as a restricted-variable and it may occupy positions in formulas appropriate to individual-variables, in argument places as well as in quantifiers. In § 2 a first-level predicate calculus, called ‘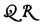‘, is presented in which the restricted-variable is an integral part.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 22 , Issue 1 , March 1957 , pp. 19 - 35
Copyright
Copyright © Association for Symbolic Logic 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hilbert, D. and Bernays, P., Grundlagen der Mathematik, Berlin (Springer), vol. 1, 1934, vol. 2, 1939.Google Scholar
[2]Hailperin, T., Quantification theory and empty individual-domains, this Journal, vol. 18 (1953), pp. 197–200.Google Scholar
[3]Quine, W. V., Quantification and the empty domain, this Journal, vol. 19 (1954), pp. 177–179.Google Scholar
[4]Rosser, Barkley, Logic for mathematicians, New York (McGraw-Hill) 1953.Google Scholar
[5]Quine, W. V., Mathematical logic, revised edition, Cambridge, Mass. (Harvard University Press), 1951.Google Scholar
[6]Wang, Hao, Existence of classes and value specification of variables, this Journal, vol. 15 (1950), pp. 103–112.Google Scholar
[7]Schmidt, Arnold, Über deduktiven Theorien mit mehreren Sorten von Grunddingen, Mathematischen Annalen, vol. 115 (1938), pp. 485–506.CrossRefGoogle Scholar
[7 ½]Schmidt, Arnold, Die Zulässigkeit der Behandlung mehrsortiger Theorien mittels der üblichen Prädikatenlogik. Mathematische Annalen, vol. 123 (1951) pp. 187–200.CrossRefGoogle Scholar
8]Wang, Hao, Logic of many-sorted theories, this Journal vol. 17 (1952), pp. 105–116.Google Scholar