Article contents
There are 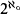 many almost strongly minimal generalized n-gons that do not interpret an infinite group
many almost strongly minimal generalized n-gons that do not interpret an infinite group
Published online by Cambridge University Press: 12 March 2014
Extract
Generalized n-gons are certain geometric structures (incidence geometries) that generalize the concept of projective planes (the nontrivial generalized 3-gons are exactly the projective planes).
In a simplified world, every generalized n-gon of finite Morley rank would be an algebraic one, i.e., one of the three families described in [9] for example. To our horror, John Baldwin [2], using methods discovered by Hrushovski [7], constructed ℵ1-categorical projective planes which are not algebraic. The projective planes that Baldwin constructed fail to be algebraic in a dramatic way.
Indeed, every algebraic projective plane over an algebraically closed field is Desarguesian [12]. In particular, an algebraically closed field (isomorphic to the base field) can be interpreted in every one of them. However, in the projective planes that Baldwin constructed, one cannot even interpret an infinite group.
In this article we show that the same phenomenon occurs for the generalized n-gons if n ≥ 3 is an odd integer. For each such n we construct 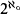 many nonisomorphic generalized n-gons of finite Morley rank that do not interpret an infinite group. As one may expect, our method is inspired by Hrushovski and Baldwin, and we follow Baldwin's line of approach. Quite often our proofs are a verification of the fact that the proofs of Baldwin [2] for n = 3 carry over to an arbitrary positive odd integer n (which is sometimes far from being obvious). As in [2], we begin by defining a certain collection of finite graphs K* and a binary relation ≤ on these graphs. We show that (K*, ≤) satisfies the amalgamation property.
many nonisomorphic generalized n-gons of finite Morley rank that do not interpret an infinite group. As one may expect, our method is inspired by Hrushovski and Baldwin, and we follow Baldwin's line of approach. Quite often our proofs are a verification of the fact that the proofs of Baldwin [2] for n = 3 carry over to an arbitrary positive odd integer n (which is sometimes far from being obvious). As in [2], we begin by defining a certain collection of finite graphs K* and a binary relation ≤ on these graphs. We show that (K*, ≤) satisfies the amalgamation property.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 3
- Cited by

