Article contents
Tree structures associated to a family of functions
Published online by Cambridge University Press: 12 March 2014
Extract
The research presented in this paper was motivated by our aim to study a problem due to J. Bourgain [3]. The problem in question concerns the uniform boundedness of the classical separation rank of the elements of a separable compact set of the first Baire class. In the sequel we shall refer to these sets (separable or non-separable) as Rosenthal compacta and we shall denote by ∝(f) the separation rank of a real-valued function f in B1(X), with X a Polish space. Notice that in [3], Bourgain has provided a positive answer to this problem in the case of K satisfying 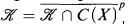 with X a compact metric space. The key ingredient in Bourgain's approach is that whenever a sequence of continuous functions pointwise converges to a function f, then the possible discontinuities of the limit function reflect a local ℓ1-structure to the sequence (fn)n. More precisely the complexity of this ℓ1-structure increases as the complexity of the discontinuities of f does. This fruitful idea was extensively studied by several authors (c.f. [5], [7], [8]) and for an exposition of the related results we refer to [1]. It is worth mentioning that A.S. Kechris and A. Louveau have invented the rank rND(f) which permits the link between the c0-structure of a sequence (fn)n of uniformly bounded continuous functions and the discontinuities of its pointwise limit. Rosenthal's c0-theorem [11] and the c0-index theorem [2] are consequences of this interaction.
with X a compact metric space. The key ingredient in Bourgain's approach is that whenever a sequence of continuous functions pointwise converges to a function f, then the possible discontinuities of the limit function reflect a local ℓ1-structure to the sequence (fn)n. More precisely the complexity of this ℓ1-structure increases as the complexity of the discontinuities of f does. This fruitful idea was extensively studied by several authors (c.f. [5], [7], [8]) and for an exposition of the related results we refer to [1]. It is worth mentioning that A.S. Kechris and A. Louveau have invented the rank rND(f) which permits the link between the c0-structure of a sequence (fn)n of uniformly bounded continuous functions and the discontinuities of its pointwise limit. Rosenthal's c0-theorem [11] and the c0-index theorem [2] are consequences of this interaction.
Passing to the case where either (fn)n are not continuous or X is a non-compact Polish space, this nice interaction is completely lost.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2005
References
REFERENCES
- 4
- Cited by

